04 集成学习 - Boosting - AdaBoost算法构建
回顾:
1、Bagging-随机森林是一个并行模型,Boosting是一个串行模型,所以Boosting模型运算效率会低一些。
2、Bagging算法解决的是模型过拟合问题,Boosting模型解决的是欠拟合问题。
十一、梯度提升迭代决策树 - GBDT
GBDT(Gradient Boosting Decison Tree 梯度提升决策树)
别名:GBT\GTB\GBRT\MART
GBDT也是Boosting算法的一种,但和AdaBoost算法不同。
● AdaBoost算法是利用前一轮的弱学习器的误差来更新样本权重值,然后一轮轮得迭代。
● GBDT也是迭代,但是GBDT要求弱学习器必须是CART模型,而且GBDT在模型训练的时候,是要求模型预测的样本损失尽可能的小。
● 作为一个提升模型,ft-1(x) 是t-1步的强分类器。t-1步的强分类器和真实值之间存在一个损失函数,即用一个损失函数衡量该模型的优劣。L(y,ft-1(x)) 代表这样的一个损失函数。
● 提升算法的思想是:下一轮迭代中再训练一个弱学习器ht(x) ;弱学习器+强学习器形成新的强学习器: ft(x) = ft-1(x)+ht(x) ;
● 第t步生成模型的损失函数:L(y,ft(x)) <=> L(y,ft-1(x)+ht(x) )
注意:只有当上一轮的损失函数达到最小后,上一轮的强模型才算训练完成。在这个基础上才能开始新一轮的迭代。所以对于第t步的模型来说,之前t-1步的模型都已经是定值。
十二、GBDT的直观理解
案例1
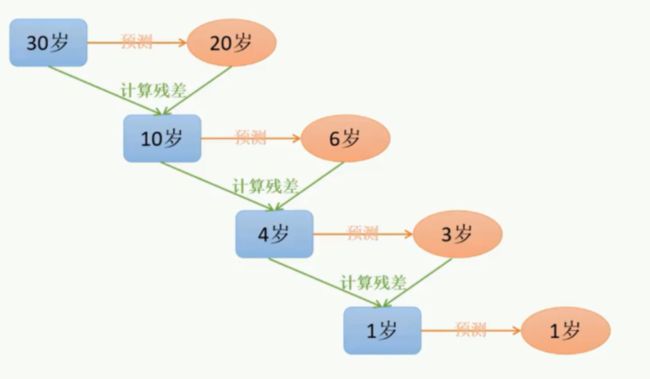
分析:现在预测样本的年龄。
1、一个样本真实值为30岁,放进决策树模型进行预测 x→y,发现预测结果 y^ 是20岁。预测值和真实值相差很大,所以现在的结果是欠拟合。现在想要改变欠拟合的现状。这里计算的残差 = 真实值-预测值 = y-y^ = 30-20 = 10。
2、对计算的残差做预测 x→(y-y^) ,发现预测结果( y-y^ )^是6岁。预测值 令y*=( y-y^ )^=6 和上一步的计算残差 y-y^=10 依然存在相对较大的偏差。计算这一步的计算残差 = 真实值-预测值 = (y-y^) - ( y-y^ )^ = y-y^-y* = 10-6 = 4
3、对计算的残差做预测 x→y-y^-y*,令 y** = (y - y^ - y*)^ =3和上一步的计算残差 y-y^-y* = 4 依然存在一点的偏差,计算这一步的计算残差 = 真实值-预测值 y-y^- y*-y**=1;
4、对计算的残差做预测 x→ y-y^- y*-y** 。这次预测值 = 真实值 ,即 y-y^- y*-y** = y*** = 1;
5、y*** =1、y** = 3、y*=6、 y^=20;累加这些值:1+3+6+20 = 30 = 真实值y。即图中红色的结果。
以上1~5的步骤就是GBDT的拟合过程。
思考: 结合上面的五个步骤,思考GBDT在拟合一种什么样的关系?
● 将每次预测后得到的计算残差作为新的预测目标,通过相同的样本X预测这个新目标,得到一个新的基学习器。
● 直到预测结果准确为止,或偏差趋向于0。
● 累加所有基学习器的预测结果,就是一步步消除误差的过程。最后得到的结果肯定等于真实值。
案例2
从决策树的角度来看GBDT是如何解决欠拟合问题的。
当给定步长的时候,给定一个步长step,在构建下一棵树的时候使用step*残差值作为输入值,这种方式可以减少过拟合的发生。
分析: 有A、B、C、D四个人,分别对应3个属性:年龄、收入、上网时长。我们希望根据收入和上网时长来预测当前这个人的年龄是多少。
A:年龄 14,收入 500,上网时间 0.5;
B:年龄 16,收入 700,上网时间 1,2;
C:年龄 24,收入 1800,上网时间 0.3;
D:年龄 26,收入 3000,上网时间 1.5;
预测步骤:
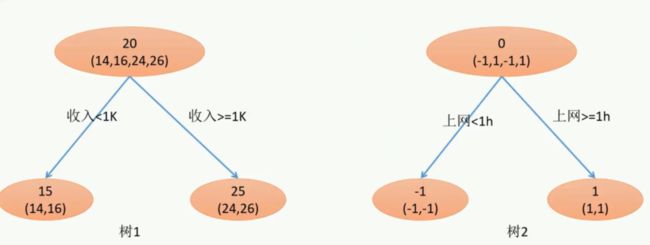
1、先看左图,左图构建的是一棵决策回归树,预测的年龄是一个连续值。每个叶子节点里放的都是目标-年龄;(一开始根节点上的20表示当前节点对年龄的预测是20岁左右,这个我们不关心。)
2、此时决策树根据收入做分支,收入小于1k的预测是15岁,收入大于等于1k的预测是25岁。
3、计算实际值和样本值之间的差,得: (A、B、C、D) 的残差 = (14-15,16-15,24-25,26-25)=(-1,1,-1,1);
PS: 为什么挑选收入作为第一个分支?
● 收入做分支时,左节点的残差的平方和(方差) = (14-15)2 +(16-15)2 = 2
如果根据上网>1和上网<1的分类结果要好:当上网>1时,年龄分别为26,16,预测值=(26+16)/2 = 42/2=21;
● 上网时间做分支时,左节点的残差的平方和(方差) = (26-21)2+(16-21)2 = 25+25=50;
所以从方差上看,选择收入作为第一个分支效果更好。
4、 将(A、B、C、D) 的残差 作为下一个模型的预测值。(A、B、C、D) 的残差 = (-1,1,-1,1)
再看右图,右图根据上网时间做分支。
A:年龄 14,收入 500,上网时间 0.5;
B:年龄 16,收入 700,上网时间 1,2;
C:年龄 24,收入 1800,上网时间 0.3;
D:年龄 26,收入 3000,上网时间 1.5;
上网<1h 的是A、C ;
上网>1h 的是B、D;
所以右图根据该属性进行划分,最终预测得到的残差为0。
5、根据模型来预测结果:
回顾GBDT的公式:f2(x) = f1(x) + h2(x) = h1(x) + h2(x) ;
当A(收入=500,上网时长=0.5) 时,f2(A) = h1(A) + h2(A) =15 -1=14;
在第一课决策树中预测的结果是15,存在一定的误差。
然后在第二棵决策树预测的结果是-1,即误差。
最后两棵树的结果相加消除了误差。
两个弱学习器的相加,变成了强学习器
最后理解一下这句话的含义:
当给定步长的时候,给定一个步长step,在构建下一棵树的时候使用step*残差值作为输入值,这种方式可以减少过拟合的发生。
最终强学习器 ft(x) = step × ∑ ht(x);
当 0
当 step>1 时,意味着我们需要比原来更少的模型就能达到预测的效果。意味着可以减少过拟合的情况。
十三、GBDT和AdaBoost的区别
AdaBoost变X: 每次改变样本数据集中的X值,预测错的加大权重,预测对的减少权重。最后再计算每次得到的基模型的权值。
GBDT变Y:本身也会改变原有数据集的数据,但他不改变X,每一个基模型输入的数值都不发生变化。但是的值会发送变化,每一步的Y都是上一个基模型的真实值和预测值之间的残差。
06 集成学习 - Boosting - GBDT算法原理、总结