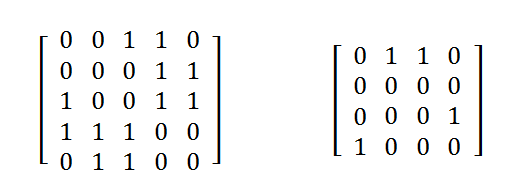1 概述#

简单的说，图由表示数据元素的集合V和表示数据之间关系的集合E组成，记为G=。图又分为有向图与无向图。下面是图的一些基本元素：

边(edge)：顶点的序偶。
顶点(vertex)：数据元素。
权重(weight)：用来表示一个顶点到另一个顶点的距离、代价、耗费等。
度(degree)：与该顶点相关联的边的数目，入度、出度等等。

无向图G1与有向图G2

图的基本类型常使用的有相邻矩阵与邻接表。下面将从两方面介绍图的储存结构与基本操作。

2 图的相邻矩阵储存类型#

图的相邻矩阵或邻接矩阵表示定点之间的邻接关系，即表示顶点之间有边或没有边的情况。如下图则是无向图G1和有向图G2的邻接矩阵。

(a)无向图G1的邻接矩阵 (b)有向图G2的邻接矩阵

相邻矩阵类型定义

对于有向图，相邻矩阵不一定对称。因为如果相邻矩阵第i行第j列的元素为1，则表示有一条从顶点vi到顶点vj的弧，而此时不一定存在由顶点vj到顶点vi的弧。

 /*图的相邻矩阵储存类型定义*/
#define MaxVertexNum 100 /*最大顶点数设为100*/
typedef enum{FALSE,TRUE} Boolean;
Boolean mark[MaxVertexNum];

typedef char VertexType; /*顶点类型设为字符型*/
typedef int EdgeType; /*边的权值设为整型*/

typedef struct {
    VertexType vexs[MaxVertexNum]; /*顶点表*/
    EdgeType edges[MaxVertexNum][MaxVertexNum]; /*邻接矩阵，即边表*/
    int numVertex,numEdge; /*顶点数和边数*/
}Mgragh,*MGragh; /*Maragh 是以邻接矩阵存储的图类型*/

图创建

首先定义相邻矩阵的尺寸，即定点数和边数。
输入每条边信息，vi为初始点，vj为终止点。将邻接表中的edges[i][j]设置为1，代表起点为i，终点为j，存在一条边。


void CreateMGraph(MGragh G){/*建立有向图G 的邻接矩阵存储*/
int i,j,k,w;
char ch;
cout<<"请输入顶点数和边数";
cin>>i>>j;
G->numVertex=i;
G->numEdge=j;

cout<<"请输入顶点信息:"<numVertex;i++) {cout<<"第"<>G->vexs[i];} /*输入顶点信息，建立顶点表*/
for (i=0;inumVertex;i++)
    for (j=0;jnumVertex;j++) 
        G->edges[i][j]=0; /*初始化邻接矩阵*/

cout<<"请输入每条边对应的两个顶点的序号:\n";

for (k=0;knumEdge;k++){
    cout<<"v:";
    cin>>i>>j; /*输入e 条边，建立邻接矩阵*/
        G->edges[i][j]=1;
            }
}

判断边类

FirstEdge即返回以v为顶点的第一条边。它的想法是：返回以顶点v的编号的相邻矩阵行，从j=0开始遍历，直到搜索到矩阵元素为1时，表示i到j有一条边，于是返回此条边。

NextEdge即返回以v为顶点的下一条边。当输入边edge时，将返回以edge.from的编号相同的矩阵行，从j=edge.to+1开始遍历，直到搜索到矩阵元素为1时，表示i到j有一条边，返回此边。


Edge FirstEdge(MGragh G,int oneVertex){
   Edge myEdge;
   myEdge.from=oneVertex;
   for(int i=0;inumVertex;i++){
       if(G->edges[oneVertex][i]!=0){
           myEdge.to=i;
           myEdge.weight=G->edges[oneVertex][i];
           break;
       }
   }
   return myEdge;
}

Edge NextEdge(MGragh G,Edge preEdge){
   Edge myEdge;
   myEdge.from =preEdge.from ;
   if(preEdge.to numVertex){
       for(int i=preEdge.to+1;inumVertex;i++){
           if(G->edges[preEdge.from][i]!=0){
               myEdge.to =i;
               myEdge.weight =G->edges[preEdge.from ][i];
               break;
           }
       }
   }
   return myEdge;
}

bool isEdge(MGragh G, Edge myEdge){
   int test=0;
   for(int i=0;inumVertex;i++){
       if(myEdge.to>=0&&G->edges[myEdge.from][myEdge.to]==1)return true;
   }
   return false;
}

两种周游算法

以有向图G2为例：

深度优先搜索的周游算法如下：假设从v0点出发，首先将v0的标志位设置为TRUE，然后从v0的第一条边出发，寻找第一条边的终点v2。因为v2为被访问过，因此将v2标志位设置为TRUE。从v2出发，寻找v2的第一条边终点为v3。因为v3为被访问过，因此设v3的标志位为TRUE。从v3出发，寻找v3的第一条边终点为v0，标志位为TRUE说明已被访问过。返回上一个顶点v2，寻找v2的nextEdge，无。返回v0，寻找v0的nextEdge，为v1，标识v1为TRUE。遍历完毕。

广度优先算法的周游如下：假设从v0出发。首先将v0的标志位设置为TRUE，将v0入队。因为队列不为空，所以取出front，设置为u，同时pop掉front。寻找v0的第一条边的终点v2。输出v2，并将其push入队列；寻找v0的第二条边的终点v1,，输出v1，并将其push入队列；寻找v0的第三条边的终点，无。返回取出front，将v2设置为u，pop掉它。寻找v2的第一条边v3，输出v3并将其push如队列；寻找v2的第二条边，无。返回取出front，将v1设置为u，pop掉它。寻找v1的第一条边，无。返回取出front，将v3设置为u，pop掉它，寻找v3的第一条边v0，因为以被访问，因此跳过；寻找v3的第二条边，无。算法结束。

//深度优先周游    
void DFS(MGragh G, int v){
    mark[v]=TRUE;
    cout<vexs[v];
    for(Edge e=FirstEdge(G,v);isEdge(G,e);e=NextEdge(G,e)){
        if(mark[e.to]==FALSE) DFS(G,e.to);
    }
}

void DFSM(MGragh G,int v){
    for(int i=0;inumVertex;i++){
        mark[i]=FALSE;
    }
    DFS(G,0);
}

//广度优先周游
void BFS(MGragh G, int v){
    for(int i=0;inumVertex;i++){
        mark[i]=FALSE;
    }
    using std::queue;
    queueQ;
    cout<vexs[v];
    mark[v]=TRUE;
    Q.push(v);
    while(!Q.empty()){
        int u=Q.front();
        Q.pop();
        for(Edge e=FirstEdge(G,u);isEdge(G,e);e=NextEdge(G,e))
            if(mark[e.to]==FALSE){
                cout<vexs[e.to];
                mark[e.to]=TRUE;
                Q.push(e.to);
            }
    }
}

3 图的邻接表储存类型#

当图中的边数较少时，相邻矩阵就会出现大量的0元素，储存这些0元素将消耗大量的储存空间。
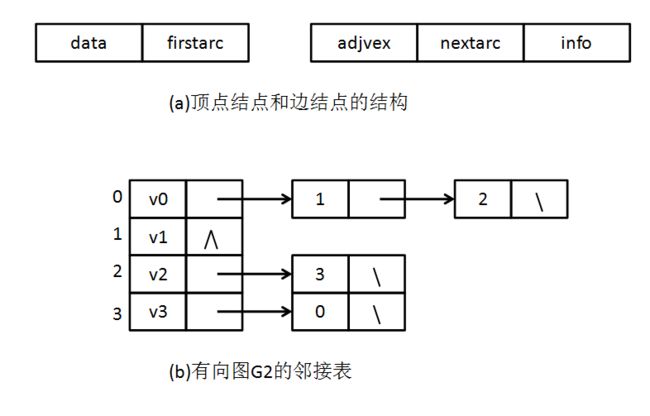
邻接表表示法是一种链式存储结构，由一个顺序储存的顶点表和n个链表储存的边表组成。顶点表目有两个域：顶点数据域和指向此顶点边表指针域。边表把依附于同一个顶点vi的边（即相邻矩阵中同一行的非0元素）组织成一个单链表。边表中的每一个表目都代表一条边，由两个主要的域组成：与顶点vi邻接的另一个顶点的序号、指向边表中下一个边表的目的指针。
顶点结点和边结点的结构如下：

Paste_Image.png

与邻接矩阵储存类型相似，邻接表的基本函数依然包括FirstEdge，NextEdge和isEdge。这里不再重复，下面只给出广度周游和深度周游算法。

邻接表类型定义

using namespace std;
#define MAX_VERTEXT_NUM 20
typedef enum{FALSE,TRUE} Boolean;
Boolean mark[MAX_VERTEXT_NUM];

typedef struct edge{     /*边定义*/
    int from,to,weight;
}Edge,*Edged;

typedef struct ArcNode{     /*边结点定义*/
    int adjvex;
    struct ArcNode *nextArc;
    int weight;
}ArcNode;

typedef struct VNode{     /*顶点定义*/
    char data;
    ArcNode *firstArc;
}VNode, AdjList[MAX_VERTEXT_NUM];

typedef struct Indegree{     /*每个点的入度*/
    int indegree;
}Indegree,indegree[MAX_VERTEXT_NUM];

typedef struct{     /*图定义*/
    AdjList verTices;
    int vexNum;
    int arcNum;
    int kind;
    indegree Indegree;
}ALGraph;

图的邻接表储存类型建立

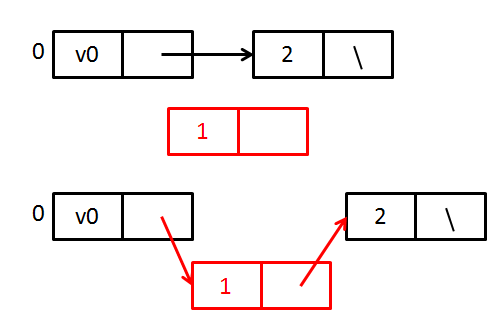
首先输入顶点和边的个数，同时申请顶点个数的结点空间。
每次输入边的邻接关系时i-j时，首先申请一个边结点空间给，结点的adjvex为j，nextarc为头结点firstarc的nextarc，头结点的firstarc变为此j结点arcnode。

邻接表插入顶点

void CreateGraph(ALGraph *G)
{
    int i,j,k,weight;
    ArcNode *arcNode;
    printf_s("请输入顶点数和边数：");
    cin>>G->vexNum;
    cin>>G->arcNum;
    //建立顶点表
    printf_s("建立顶点表\n");
    for (i = 0; i < G->vexNum; i++)
    {
        printf_s("请输入第%d个顶点:", i);
        cin>>G->verTices[i].data;
        arcNode = (ArcNode *)malloc(sizeof(ArcNode));
        arcNode->adjvex=i;
        arcNode->nextArc=NULL;
        G->verTices[i].firstArc=arcNode;
        G->Indegree[i].indegree=0;
    }
    //建立边表
    printf_s("建立边表\n");
    for (k = 0; k < G->arcNum; k++)
    {
        printf_s("请输入（vi-vj）的顶点对序号");
        cin>>i;
        cin>>j;
        arcNode = (ArcNode *)malloc(sizeof(ArcNode));
        arcNode->adjvex = j;
        arcNode->nextArc = G->verTices[i].firstArc->nextArc;//插入表头
        G->verTices[i].firstArc ->nextArc= arcNode;
        G->Indegree[j].indegree++;
    }
}

两种周游算法

深度优先周游：对于邻接表存储类型，它采用递归算法，从起始点v0沿着邻接表一次访问，直到next指针为NULL，则返回上一层，进入上一层顶点v1所在的链表继续逐个访问。

广度周游与相邻矩阵法类似，这里不做阐述。算法如下：

//深度优先周游
void DFSM(ALGraph *G,int i){
    ArcNode *p;
    cout<verTices[i].data;
    mark[i]=TRUE;
    p=G->verTices[i].firstArc;
    while(p){
        if(mark[p->adjvex]==FALSE)
            DFSM(G,p->adjvex);
        p=p->nextArc;       
    }
}

void DFS(ALGraph *G){
    for ( int i=0; ivexNum;i++)
        mark[i]=FALSE;
    for( int i=0; ivexNum;i++)
        if(!mark[i])
            DFSM(G,i);
}

//广度优先周游
void BFS(ALGraph *G,int x){
    ArcNode *p;
    int w;
    using std::queue;
    queue Q;
    for ( int i=0; ivexNum;i++) {mark[i]=FALSE;}
    cout<verTices[x].data;
    mark[x]=TRUE;
    Q.push(x);
    while(!Q.empty()){
        int v=Q.front();
        Q.pop();
        p=G->verTices[v].firstArc;
        while(p){
            int w=p->adjvex;
            if(mark[w]==FALSE){
                mark[w]=TRUE;
                cout<verTices[w].data;
                Q.push(w);}
            p=p->nextArc;
            }
        }
}

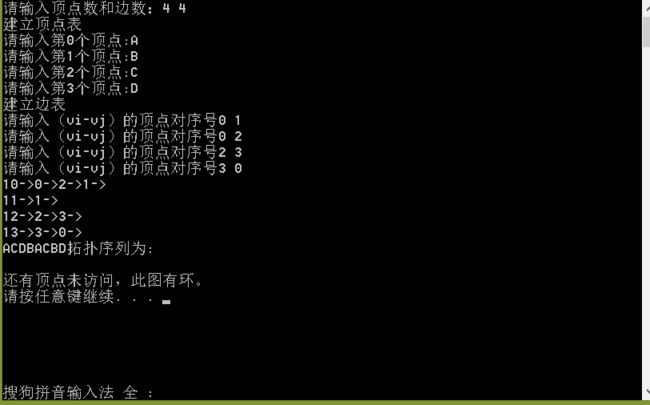
拓扑排序

有向图的边可以看做定点之间制约关系的描述。在工程实践中，有些工程的进行经常受到一定条件的约束，例如一个工程项目通常由若干子工程组成，某些子工程完成之后另一些子工程才能开始。

一个无环的有向图称为有向无环图，有向无环图常用来描述一个过程或一个系统的进行过程。对于有向无环图G=，如果顶点序列满足：存在顶点vi到vj的一条路径，那么在序列中顶点vi必在顶点vj之前，顶点集合V的这种线型序列称作一个拓扑序列。

进行有向图的拓扑序列方法如下：

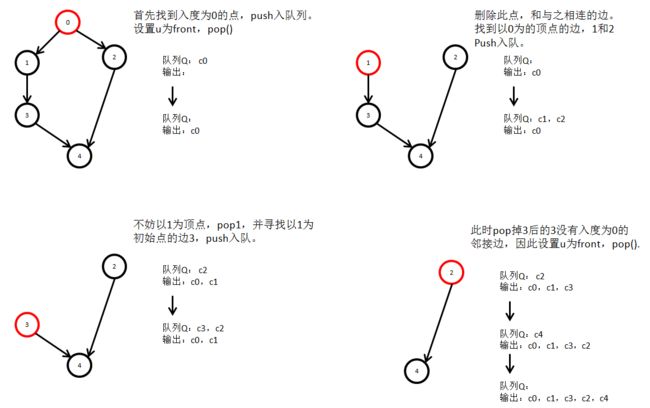
从有向图中选出一个没有前驱（入度为0）的顶点并输出。
删除图中该顶点和所有以它为起点的弧。

不断重复上述两个步骤，会出现两种情形：要么有向图中顶点全部被输出，要么当前图中不存在没有前驱的顶点。当图中的顶点全部输出时，就完成了有向无环图的拓扑排序；当图中还有顶点没有输出时，说明有向图中含有环。

它的工作思想如下：

拓扑排序


//拓扑排序
void TopsortbyQueue(ALGraph*G){
    for(int i=0; i< G->vexNum;i++)
        mark[i]=FALSE;
    using std::queue;
    queue Q;
    cout<<"拓扑序列为:"<vexNum;i++){
        if(G->Indegree[i].indegree==0)
            Q.push(i);}
        while(!Q.empty()){
            int v=Q.front();
            Q.pop();
            cout<Indegree[e.to].indegree--;
                if(G->Indegree[e.to].indegree ==0)
                    Q.push(e.to);
            }
        }
        for(int i=0;i< G->vexNum;i++)
            if(mark[i]==FALSE){
                cout<

 
 4 总结# 
 明显感觉到写得多了对于语言的运用更熟练了，也更有了设计算法需要的逻辑思想。这个写的还算比较顺_{随着思维和语言能力提升，希望能在acm校选赛比赛上有好的发挥}过两天来更新结果！ 
 5 附录# 
 邻接矩阵： 
  
   
    
     
    
   
  
    邻接矩阵测试结果 
   
  
 #include
#include
#include
#include 
using namespace std;

#define MaxVertexNum 100 /*最大顶点数设为100*/
typedef enum{FALSE,TRUE} Boolean;
Boolean mark[MaxVertexNum];

typedef char VertexType; /*顶点类型设为字符型*/
typedef int EdgeType; /*边的权值设为整型*/

typedef struct {
    VertexType vexs[MaxVertexNum]; /*顶点表*/
    EdgeType edges[MaxVertexNum][MaxVertexNum]; /*邻接矩阵，即边表*/
    int numVertex,numEdge; /*顶点数和边数*/
}Mgragh,*MGragh; /*Maragh 是以邻接矩阵存储的图类型*/


typedef struct edge{
    int from,to,weight;
}Edge,*Edged;

void CreateMGraph(MGragh G){/*建立有向图G 的邻接矩阵存储*/
int i,j,k,w;
char ch;
cout<<"请输入顶点数和边数";
cin>>i>>j;
G->numVertex=i;
G->numEdge=j;

cout<<"请输入顶点信息:"<numVertex;i++) {cout<<"第"<>G->vexs[i];} /*输入顶点信息，建立顶点表*/
for (i=0;inumVertex;i++)
    for (j=0;jnumVertex;j++) 
        G->edges[i][j]=0; /*初始化邻接矩阵*/

cout<<"请输入每条边对应的两个顶点的序号:\n";

for (k=0;knumEdge;k++){
    cout<<"v:";
    cin>>i>>j; /*输入e 条边，建立邻接矩阵*/
        G->edges[i][j]=1;
            }
}

void displaygraph(MGragh G){
int i,j;

for(i=0;inumVertex;i++){
    for(j=0;jnumVertex;j++){
        cout<edges[i][j]<<" ";}
    cout<numVertex;i++){
        if(G->edges[oneVertex][i]!=0){
            myEdge.to=i;
            myEdge.weight=G->edges[oneVertex][i];
            break;
        }
    }
    return myEdge;
}

Edge NextEdge(MGragh G,Edge preEdge){
    Edge myEdge;
    myEdge.from =preEdge.from ;
    if(preEdge.to numVertex){
        for(int i=preEdge.to+1;inumVertex;i++){
            if(G->edges[preEdge.from][i]!=0){
                myEdge.to =i;
                myEdge.weight =G->edges[preEdge.from ][i];
                break;
            }
        }
    }
    return myEdge;
}

bool isEdge(MGragh G, Edge myEdge){
    int test=0;
    for(int i=0;inumVertex;i++){
        if(myEdge.to>=0&&G->edges[myEdge.from][myEdge.to]==1)return true;
    }
    return false;
}

//深度优先周游    
void DFS(MGragh G, int v){
    mark[v]=TRUE;
    cout<vexs[v];
    for(Edge e=FirstEdge(G,v);isEdge(G,e);e=NextEdge(G,e)){
        if(mark[e.to]==FALSE) DFS(G,e.to);
    }
}

void DFSM(MGragh G,int v){
    for(int i=0;inumVertex;i++){
        mark[i]=FALSE;
    }
    DFS(G,0);
}

//广度优先周游
void BFS(MGragh G, int v){
    for(int i=0;inumVertex;i++){
        mark[i]=FALSE;
    }
    using std::queue;
    queueQ;
    cout<vexs[v];
    mark[v]=TRUE;
    Q.push(v);
    while(!Q.empty()){
        int u=Q.front();
        Q.pop();
        for(Edge e=FirstEdge(G,u);isEdge(G,e);e=NextEdge(G,e))
            if(mark[e.to]==FALSE){
                cout<vexs[e.to];
                mark[e.to]=TRUE;
                Q.push(e.to);
            }
    }
}

int main(){
    Mgragh *Graph = (Mgragh *)malloc(sizeof(Mgragh));
    CreateMGraph(Graph);
    displaygraph(Graph);
    cout<
 
 邻接表 
  
   
    
     
    
   
  
    邻接表 
   
  
 #include
#include
#include
#include 
using namespace std;
#define MAX_VERTEXT_NUM 20
typedef enum{FALSE,TRUE} Boolean;
Boolean mark[MAX_VERTEXT_NUM];

typedef struct edge{
    int from,to,weight;
}Edge,*Edged;

typedef struct ArcNode{
    int adjvex;
    struct ArcNode *nextArc;
    int weight;
}ArcNode;

typedef struct VNode{
    char data;
    ArcNode *firstArc;
}VNode, AdjList[MAX_VERTEXT_NUM];

typedef struct Indegree{
    int indegree;
}Indegree,indegree[MAX_VERTEXT_NUM];

typedef struct{
    AdjList verTices;
    int vexNum;
    int arcNum;
    int kind;
    indegree Indegree;
}ALGraph;

typedef struct Dist{
    int index;
    int length;
    int pre;
}Dist,*Dijk;

edge FirstEdge(ALGraph *G,int oneVertex){
    Edge myEdge;
    myEdge.from=oneVertex;
    ArcNode *temp=G->verTices[oneVertex].firstArc;
    if(temp->nextArc!=NULL){
        myEdge.to=temp->nextArc->adjvex;
        myEdge.weight=temp->nextArc->weight;
    }
    return myEdge;
}

edge NextEdge(ALGraph *G,Edge preEdge){
    Edge myEdge;
    myEdge.from =preEdge.from;
    ArcNode *temp=G->verTices[preEdge.from].firstArc;
    while(temp->nextArc!=NULL&&temp->adjvex<=preEdge.to)
        temp=temp->nextArc;
    if(temp->nextArc!=NULL){
        myEdge.to=temp->nextArc->adjvex;
        myEdge.weight=temp->nextArc->weight;
    }
    return myEdge;
}

bool isEdge(ALGraph *G, Edge myEdge){
    int n=0;
    ArcNode *p;
    p=G->verTices[myEdge.from].firstArc;
    while(p){
        if(p->adjvex==myEdge.to){
            n=0;
        }else{
            n=1;
        }
        p=p->nextArc;
    }
    if(n==0){return true;}
    else{
        return false;
    }
}

void CreateGraph(ALGraph *G)
{
    int i,j,k,weight;
    ArcNode *arcNode;
    printf_s("请输入顶点数和边数：");
    cin>>G->vexNum;
    cin>>G->arcNum;
    //建立顶点表
    printf_s("建立顶点表\n");
    for (i = 0; i < G->vexNum; i++)
    {
        printf_s("请输入第%d个顶点:", i);
        cin>>G->verTices[i].data;
        arcNode = (ArcNode *)malloc(sizeof(ArcNode));
        arcNode->adjvex=i;
        arcNode->nextArc=NULL;
        G->verTices[i].firstArc=arcNode;
        G->Indegree[i].indegree=0;
    }
    //建立边表
    printf_s("建立边表\n");
    for (k = 0; k < G->arcNum; k++)
    {
        printf_s("请输入（vi-vj）的顶点对序号");
        cin>>i;
        cin>>j;
        arcNode = (ArcNode *)malloc(sizeof(ArcNode));
        arcNode->adjvex = j;
        arcNode->nextArc = G->verTices[i].firstArc->nextArc;//插入表头
        G->verTices[i].firstArc ->nextArc= arcNode;
        G->Indegree[j].indegree++;
    }
}

//显示图的邻接表
void DisplayGraph(ALGraph *G)
{
    int i;
    for (i = 0; i < G->vexNum; i++)
    {
            cout<Indegree[i].indegree;
            ArcNode *P= G->verTices[i].firstArc;
            printf_s("%d->", i);
        while (P != NULL)
        {
            printf_s("%d->", P->adjvex);
            P = P->nextArc;
        }
        printf_s("\n");
    }
}

//深度优先周游
void DFSM(ALGraph *G,int i){
    ArcNode *p;
    cout<verTices[i].data;
    mark[i]=TRUE;
    p=G->verTices[i].firstArc;
    while(p){
        if(mark[p->adjvex]==FALSE)
            DFSM(G,p->adjvex);
        p=p->nextArc;       
    }
}

void DFS(ALGraph *G){
    for ( int i=0; ivexNum;i++)
        mark[i]=FALSE;
    for( int i=0; ivexNum;i++)
        if(!mark[i])
            DFSM(G,i);
}

//广度优先周游
void BFS(ALGraph *G,int x){
    ArcNode *p;
    int w;
    using std::queue;
    queue Q;
    for ( int i=0; ivexNum;i++) {mark[i]=FALSE;}
    cout<verTices[x].data;
    mark[x]=TRUE;
    Q.push(x);
    while(!Q.empty()){
        int v=Q.front();
        Q.pop();
        p=G->verTices[v].firstArc;
        while(p){
            int w=p->adjvex;
            if(mark[w]==FALSE){
                mark[w]=TRUE;
                cout<verTices[w].data;
                Q.push(w);}
            p=p->nextArc;
            }
        }
}

//拓扑排序
void TopsortbyQueue(ALGraph*G){
    for(int i=0; i< G->vexNum;i++)
        mark[i]=FALSE;
    using std::queue;
    queue Q;
    cout<<"拓扑序列为:"<vexNum;i++){
        if(G->Indegree[i].indegree==0)
            Q.push(i);}
        while(!Q.empty()){
            int v=Q.front();
            Q.pop();
            cout<Indegree[e.to].indegree--;
                if(G->Indegree[e.to].indegree ==0)
                    Q.push(e.to);
            }
        }
        for(int i=0;i< G->vexNum;i++)
            if(mark[i]==FALSE){
                cout<

图的存储结构——邻接矩阵与邻接表

1 概述#

2 图的相邻矩阵储存类型#

3 图的邻接表储存类型#

4 总结#

5 附录#

你可能感兴趣的:(图的存储结构——邻接矩阵与邻接表)