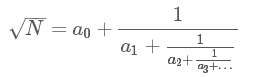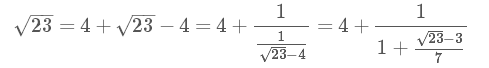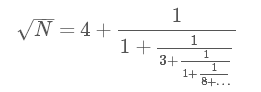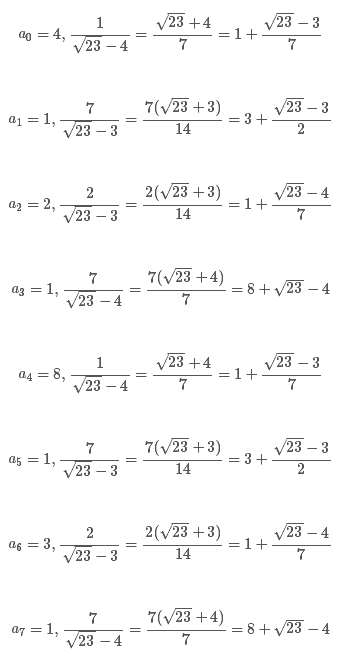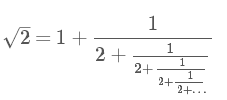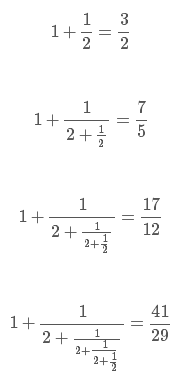问题56-60参见: https://www.jianshu.com/p/8573b8aeaa3b
61、循环多边形数
三角形数、正方形数、五边形数、六边形数、七边形数和八边形数统称为多边形数。它们分别由如下的公式给出:
三角形数 P3(n)=n(n+1)/2 1, 3, 6, 10, 15, …
正方形数 P4(n)=n2 1, 4, 9, 16, 25, …
五边形数 P5(n)=n(3n−1)/2 1, 5, 12, 22, 35, …
六边形数 P6(n)=n(2n−1) 1, 6, 15, 28, 45, …
七边形数 P7(n)=n(5n−3)/2 1, 7, 18, 34, 55, …
八边形数 P8(n)=n(3n−2) 1, 8, 21, 40, 65, …
由三个4位数8128、2882、8281构成的有序集有如下三个有趣的性质:
1:这个集合是循环的,每个数的后两位是后一个数的前两位(最后一个数的后两位也是第一个数的前两位);
2:每种多边形数——三角形数(P3(127)=8128)、正方形数(P4(91)=8281)和五边形数(P5(44)=2882)——在其中各有一个代表;
3:这是唯一一个满足上述性质的4位数有序集;
存在唯一一个包含六个4位数的有序循环集,每种多边形数——三角形数、正方形数、五边形数、六边形数、七边形数和八边形数——在其中各有一个代表。求这个集合的元素和。
Python3解答
# 三角数n*(1*n-(-1))/2、四方数n*(2*n-0)/2
# 五星数n*(3*n-1)/2、六点数n*(4*n-2)/2
# 七顶数n*(5*n-3)/2、八边数n*(6*n-4)/2
# 综合函数
def All(n, m): # m代表三、四……八
return n * ((m - 2) * n - (m - 4)) / 2
# 函数名称集合
FuncSet = ['Triangle', 'Square', 'Pentagon', 'Heptagon', 'Hexagon', 'Octagon']
# 四位数第三位不为0的数字分裂字典
def NumSet(func, m):
fset = {}
hu = 1
while len(str(int(func(hu, m)))) < 5:
cc = str(int(func(hu, m)))
if len(cc) == 4 and cc[2] != '0': # 四位数中的十位数不能为0
if int(cc[:2]) not in fset:
fset[int(cc[:2])] = [int(cc[2:])]
else:
fset[int(cc[:2])].append(int(cc[2:])) # 前2位数字相同的
hu += 1
return fset
# 开始计算每个函数的字典集合
Set = locals()
for an in [5, 4, 3, 2, 0, 1]:
Set['%s' % FuncSet[an]] = NumSet(All, an + 3)
# 无法判断这几个数字分别是什么型的函数
# 需要遍历所有组合
# 但是不必全排列,因为1234、2341、3412,4123都是一样的
from itertools import permutations
zuhe = []
for j in permutations(FuncSet[1:]):
zuhe.append([FuncSet[0]] + list(j)) # 固定一个,后面的全排列
# 递推函数
def Re(result, funlist, zuhelist):
if len(result) == 6:
if result[0][0] == result[-1][-1]:
print(funlist)
return result
else:
return False
else: # 需要继续添加
for hg in zuhelist:
if result[-1][-1] in eval(hg):
for hu in eval(hg)[result[-1][-1]]:
dd = result.copy()
dd.append([result[-1][-1], hu])
rr = funlist.copy()
rr.append(hg)
ss = zuhelist.copy()
ss.remove(hg)
ff = Re(dd, rr, ss)
if ff:
return ff
else:
continue
return False
# 开始
for huus in zuhe: # 遍历每一种可能性
# 记录数据
record = []
# 记录函数
func = []
# 选取起始的数据
for start in eval(huus[0]):
record = eval(huus[0])[start]
func = [huus[0]]
for jj in record:
result = Re([[start, jj]], func, huus[1:])
if not result:
continue
else:
# 已经得出结果计算值
print(result)
summ = 0
for num in result:
summ += int(str(num[0]) + str(num[1]))
break
break
print(summ)
答案:数分别是:[[82, 56], [56, 25], [25, 12], [12, 81], [81, 28], [28, 82]]
数对应的类型:['Triangle', 'Square', 'Hexagon', 'Octagon', 'Heptagon', 'Pentagon']
总和:28684
62、重排立方数
立方数41063625=345^3 可以重排为另外两个立方数:
56623104=384^3
66430125=405^3
实际上,41063625是重排中恰好有三个立方数的最小立方数。
求重排中恰好有五个立方数的最小立方数。
Python3解答
#将数转化为重排后的最大值
def NumToStr(number):
lists=sorted(list(str(number)),reverse=True)
strs=''.join(lists)
return strs
#开始计算
exdict={}
long=[]
num=1
while len(long)<6:
sf=NumToStr(int(num**3))
if sf in exdict:
exdict[sf].append(num)
else:
exdict[sf]=[num]
long=max(exdict.items(),key=lambda x:len(x[1]))[1]
num+=1
if len(long)==5:#如果有5个了,在退出循环
for ggg in long:
print('%d^3 = %d'%(ggg, ggg ** 3))
print('最小的数:%d'%(long[0]**3))
break
答案:五个数分别是:
5027^3 = 127035954683
7061^3 = 352045367981
7202^3 = 373559126408
8288^3 = 569310543872
8384^3 = 589323567104
最小的数:127035954683
63、幂与位数
5位数16807=7^5同时也是一个数的五次幂。同样的,9位数134217728=8^9同时也是九次幂。
有多少个n位正整数同时也是n次幂。
Python3解答
#个数
count=0
#位数从1开始
weishu=1
while 1:
low=10**(weishu-1)#几位数的下限
up=10**weishu-1#几位数的上限
sboot=low**(1/(weishu))#下限的方根
#获得sboot与9之间的整数个数
dd=9-int(sboot)
if dd==0:
print(count)
break
else:
if int(sboot)-sboot==0:
count+=dd+1
else:
count+=dd
weishu+=1
答案:49
64、奇周期平方根
所有的平方根写成如下连分数表示时都是周期性重复的:
例如,计算√23:
如果继续计算下去,可得到如下的展开:
整个过程可以总结如下:
从上面式子,不难看出序列正在重复。将其简记为 √23 = [4;(1,3,1,8)],表示在此之后(1,3,1,8)无限循环。
前10个(无理数)平方根的连分数表示是:
√2=[1;(2)],周期=1
√3=[1;(1,2)],周期=2
√5=[2;(4)],周期=1
√6=[2;(2,4)],周期=2
√7=[2;(1,1,1,4)],周期=4
√8=[2;(1,4)],周期=2
√10=[3;(6)],周期=1
√11=[3;(3,6)],周期=2
√12= [3;(2,6)],周期=2
√13=[3;(1,1,1,1,6)],周期=5
在N ≤ 13中,恰好有4个连分数(斜体)表示的周期是奇数。
在N ≤ 10000中,有多少个连分数表示的周期是奇数。
Python3解答
#定义函数
def Get(number):
#计算平方根
dd=number**0.5
#取整,确定开始值
start=int(dd)
#存储值、和周期值
peilist=[[start],[]]
#存储每一次的中间过程
middle=[]
#第一个中间过程
fenzi=1
sfenmu=number
sign=-start
first=[fenzi,sfenmu,sign]
while first not in middle:
middle.append(first)
hhd=middle[-1][1]-middle[-1][2]**2#分母
#分子总系数
fenziall=middle[-1][0]*(start-middle[-1][2])
#值
num=int(fenziall/hhd)
peilist[-1].append(num)
#周期值
fenzi=int(hhd/middle[-1][0])
sfenmu=number
sign=int((-middle[-1][2])-fenzi*num)
first=[fenzi,sfenmu,sign]
return number,peilist #返回值和周期值
#开始计算
count=0
for i in range(1,10001):
ss=i**0.5
if int(ss)-ss!=0:
dd=Get(i)
if len(dd[-1][-1])%2==1:
count+=1
print(count)
答案:1322
65、e的有理逼近
2的算术平方根可以写成无限连分数的形式:
这个无限连分数可以简记为 √2 = [1;(2)],其中(2)表示2无限重复。同样的,我们可以记√23 = [4;(1,3,1,8)]。
可以证明,截取算术平方根连分数表示的一部分所组成的序列,给出了一系列最佳有理逼近值。让我们来考虑√2的逼近值:
因此√2的前十个逼近值为:
1, 3/2, 7/5, 17/12, 41/29, 99/70, 239/169, 577/408, 1393/985, 3363/2378, …
最令人惊讶的莫过于重要的数学常数e有如下连分数表示:
e = [2; 1,2,1, 1,4,1, 1,6,1 , … , 1,2k,1, …]
e的前十个逼近值为:
2, 3, 8/3, 11/4, 19/7, 87/32, 106/39, 193/71, 1264/465, 1457/536, …第10个逼近值的分子各位数字之和为1+4+5+7=17。
求e的第100个逼近值的分子各位数字之和。
Python3解答
def Computer(n):#n表示第几位
if n==1:
return 2,1
elif n==2:
return 3,1
else:
#计算属于第几个值
#除去前2个值
dd=n-2
#列出n位之前经历的数字,例如第5位就是[1,1,2,1,2].从后往前
#例如第6位就是[4,1,1,2,1,2]
shuzilist=[2,1]#开始的2位
for ii in range(dd):
if ii%3==0:
shuzilist.append((int(ii/3)+1)*2)
else:
shuzilist.append(1)
slist=shuzilist[::-1]
#其中slist中的第一位是起始数据
fenmu=slist[0]
fenzi=1
for shuzi in slist[1:]:
fenzi=fenmu*shuzi+fenzi#计算加法
fenmu,fenzi=fenzi,fenmu#计算倒数
return fenmu,fenzi
for jj in range(1, 14):
fenshu = Computer(jj)
print('第%s个逼近值:%d / %d'%(jj, fenshu[0], fenshu[1]))
result=Computer(100)[0]
print('第100位的分子数字和为:%d'%sum([int(x) for x in list(str(result))]))
答案:第1个逼近值:2 / 1
第2个逼近值:3 / 1
第3个逼近值:8 / 3
第4个逼近值:11 / 4
第5个逼近值:19 / 7
第6个逼近值:87 / 32
第7个逼近值:106 / 39
第8个逼近值:193 / 71
第9个逼近值:1264 / 465
第10个逼近值:1457 / 536
第11个逼近值:2721 / 1001
第12个逼近值:23225 / 8544
第13个逼近值:25946 / 9545
第100位的分子数字和为:272
持续更新,欢迎讨论,敬请关注!!!