在理解二分搜索树之前,我们先来看看二叉树是什么。
1.1 二叉树
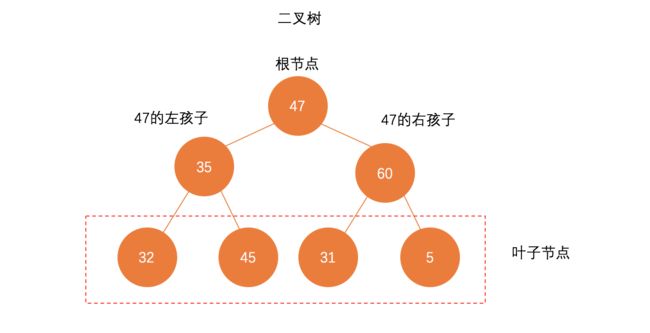
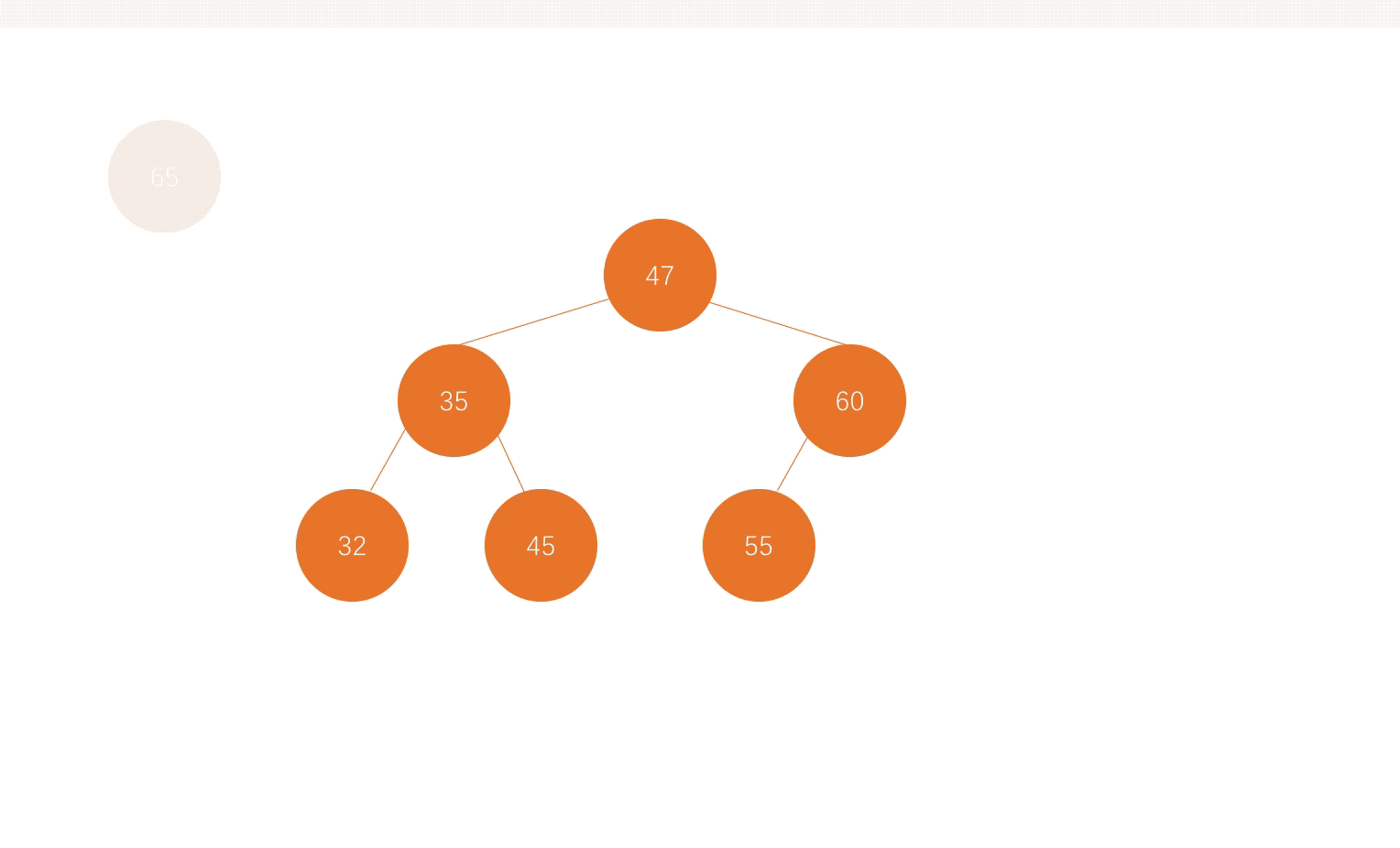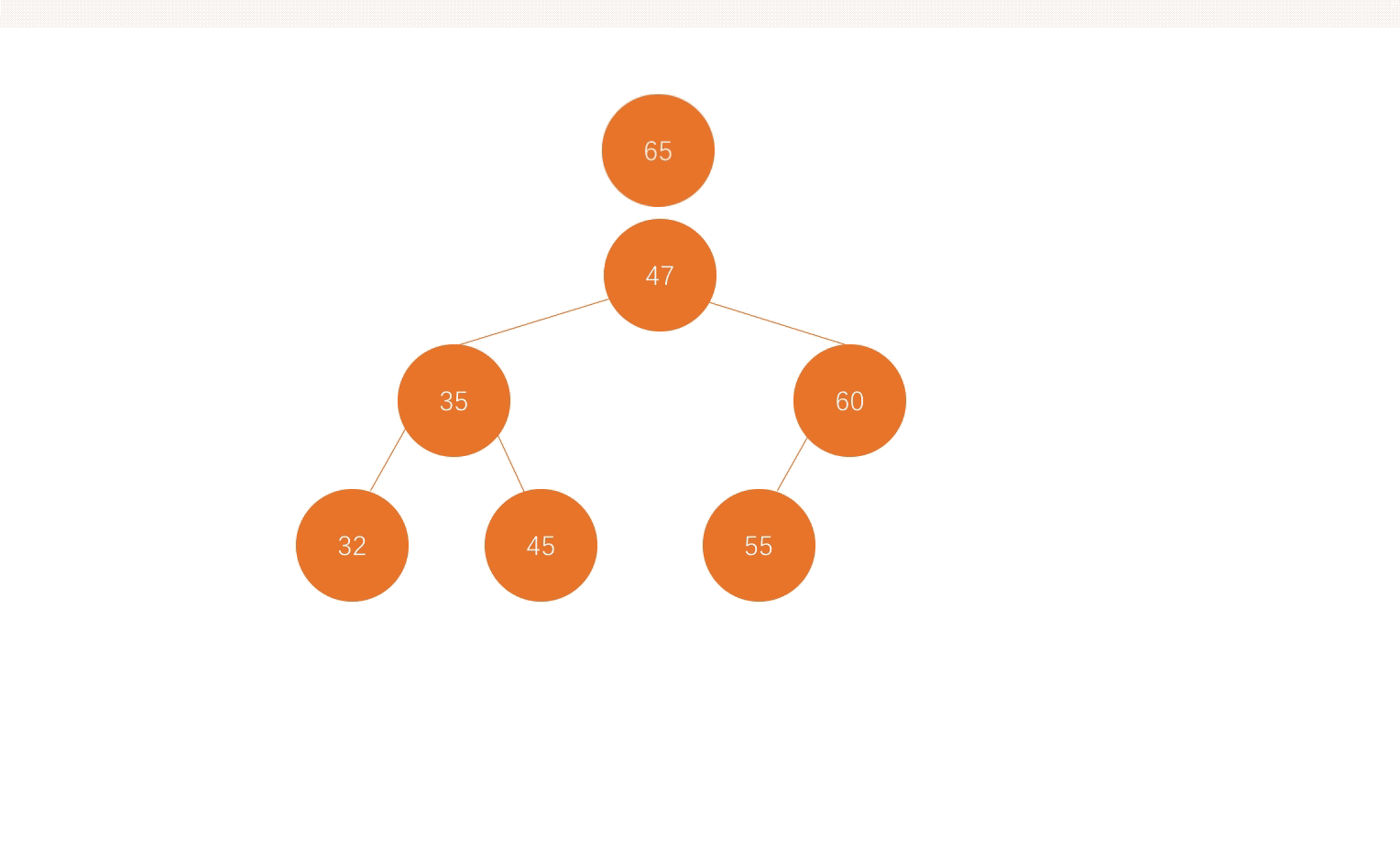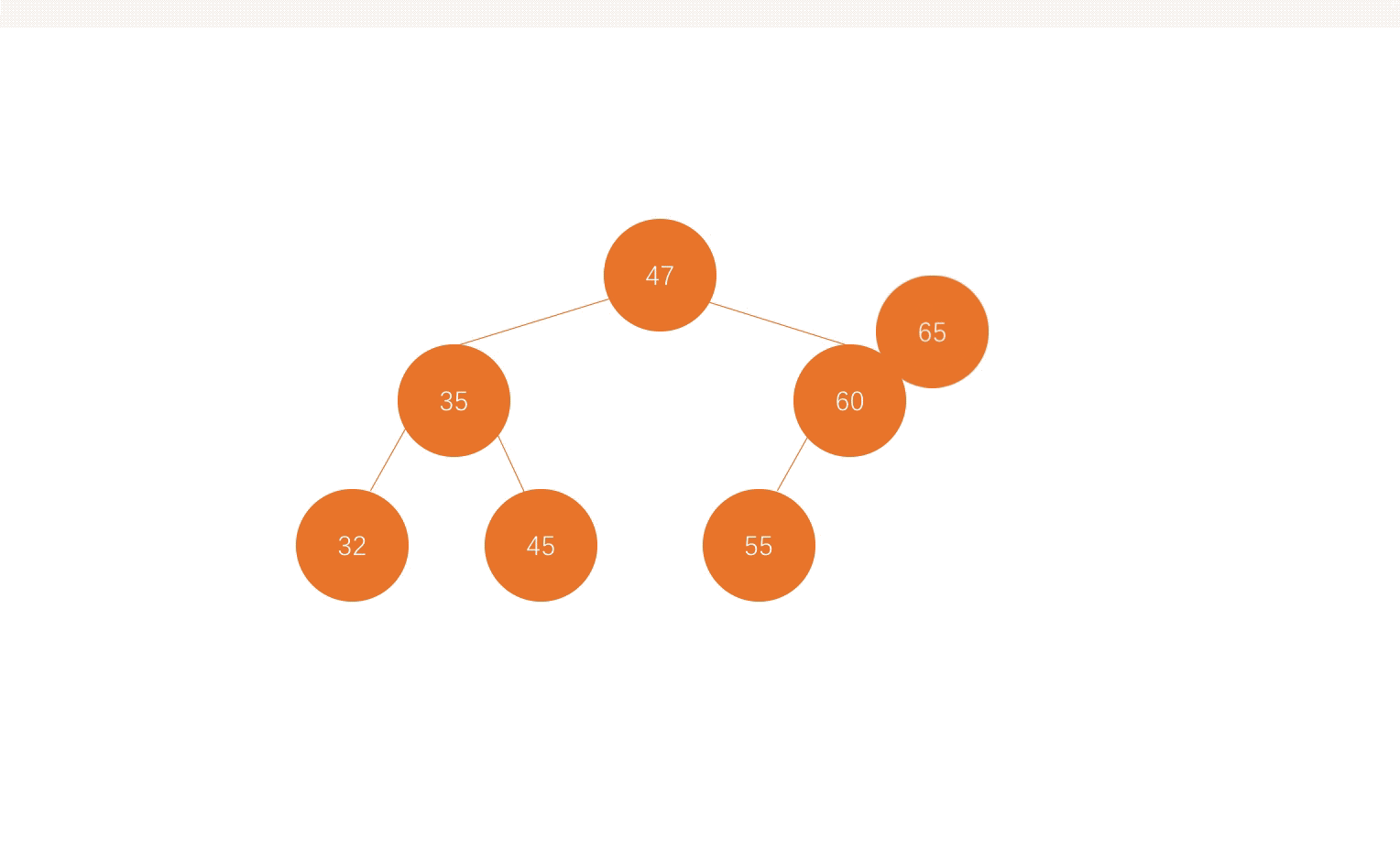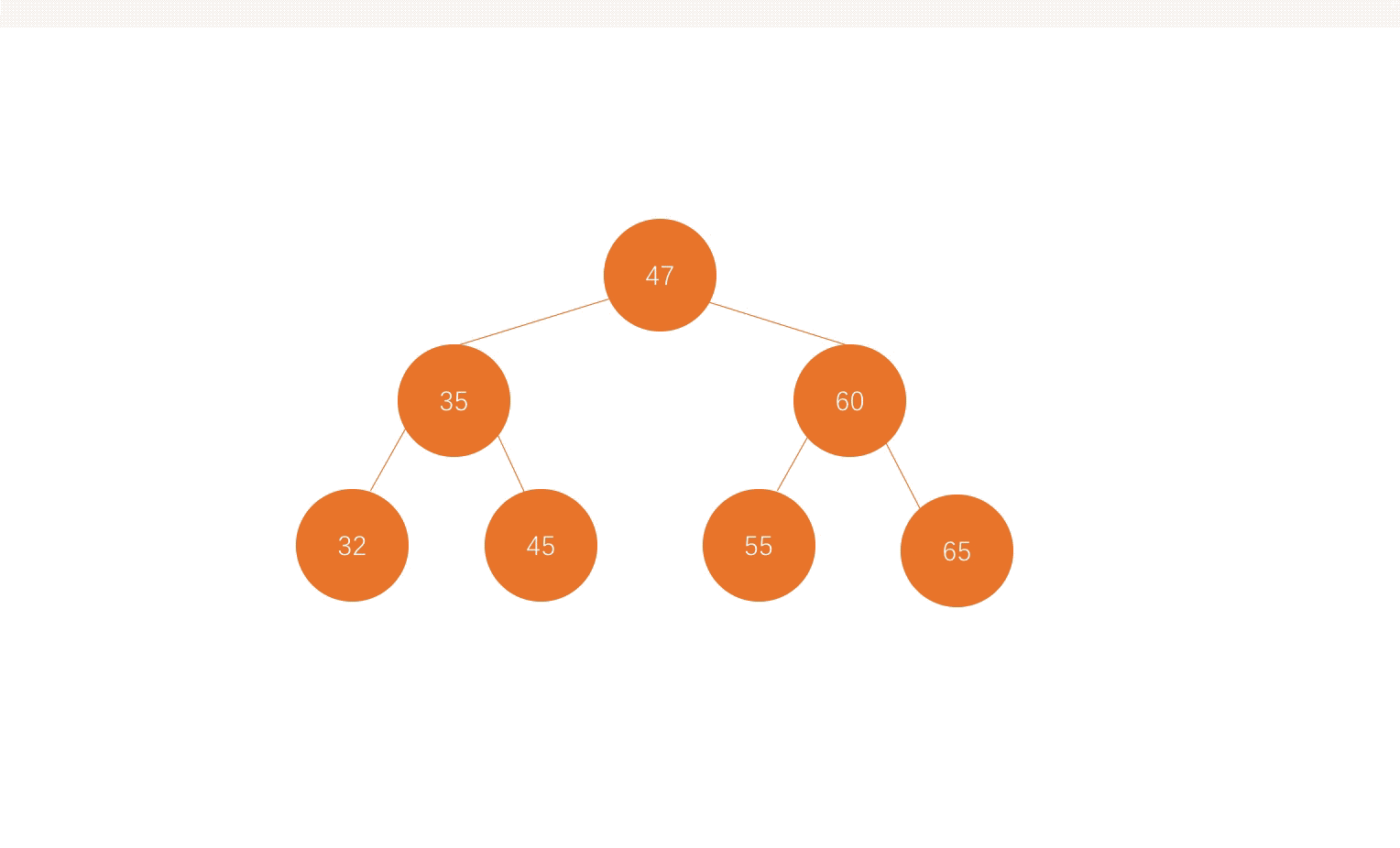
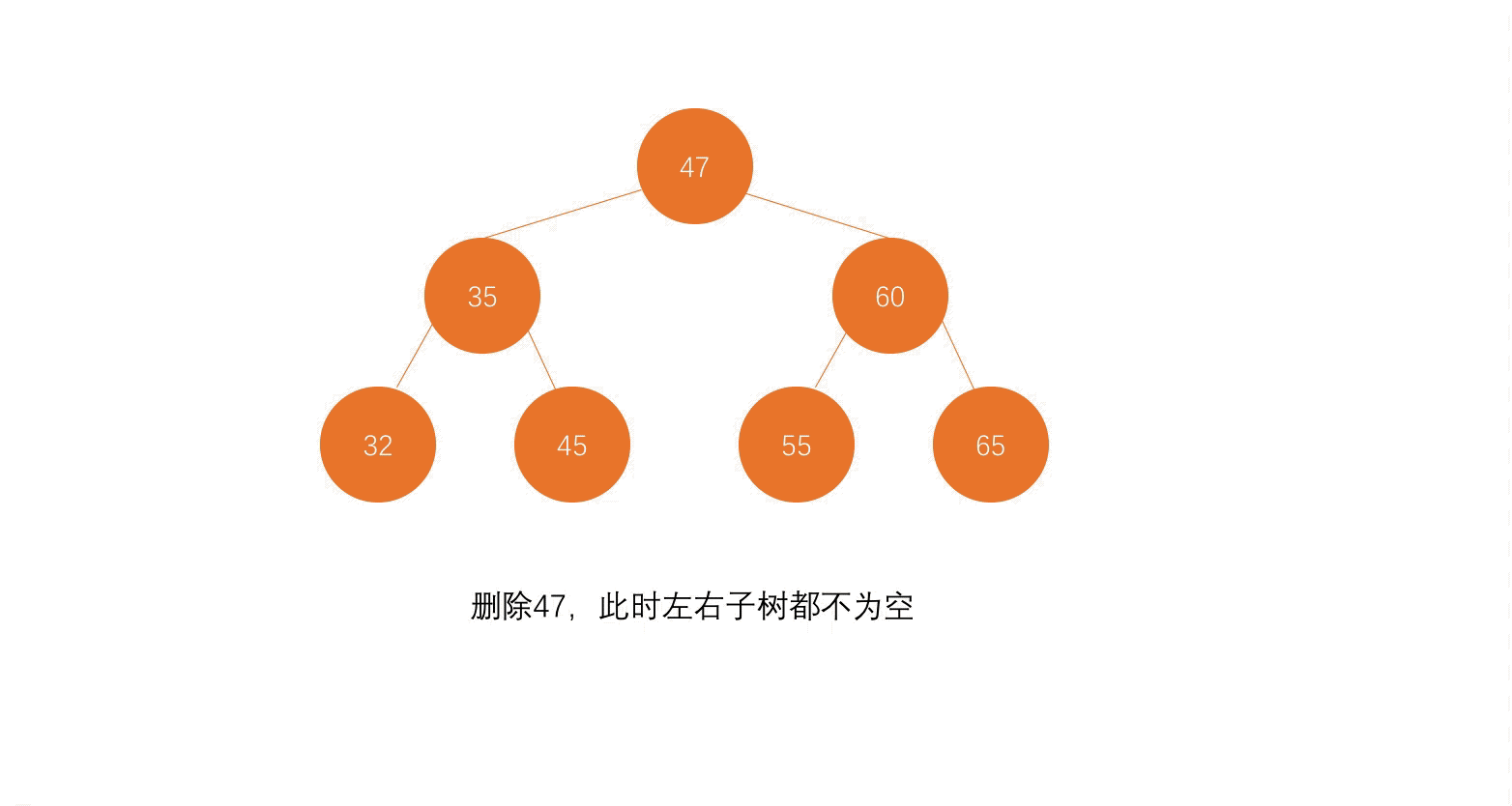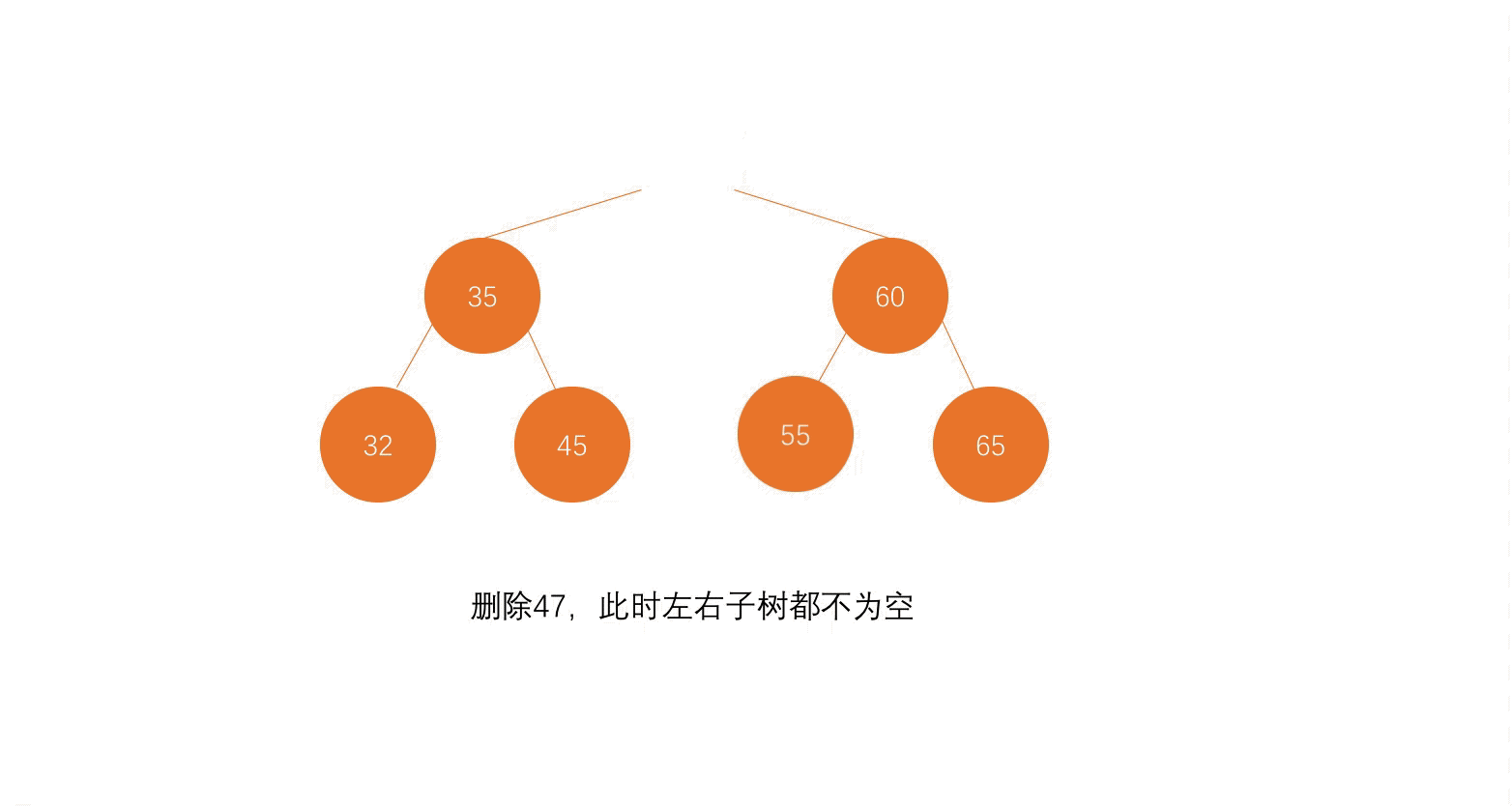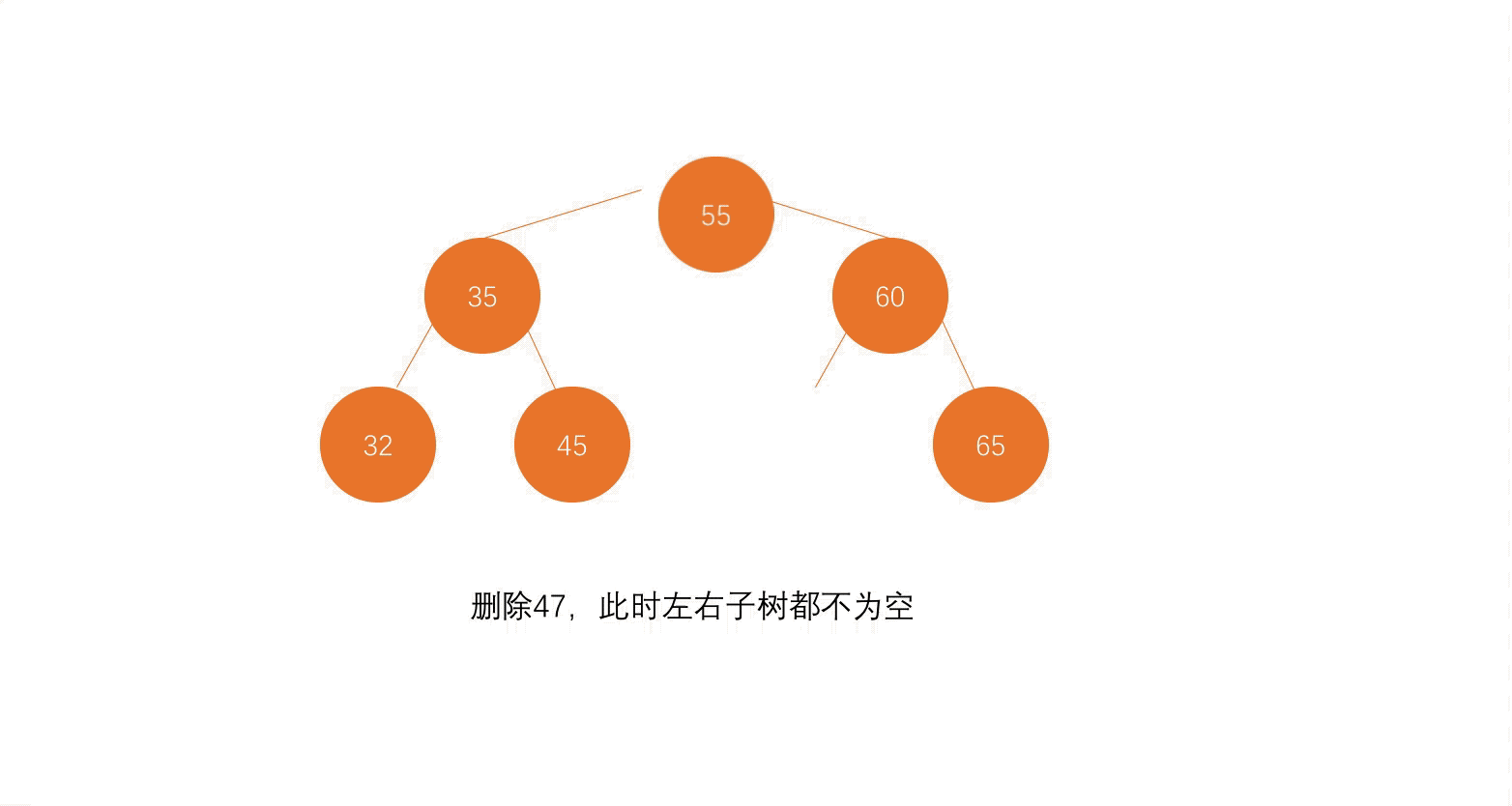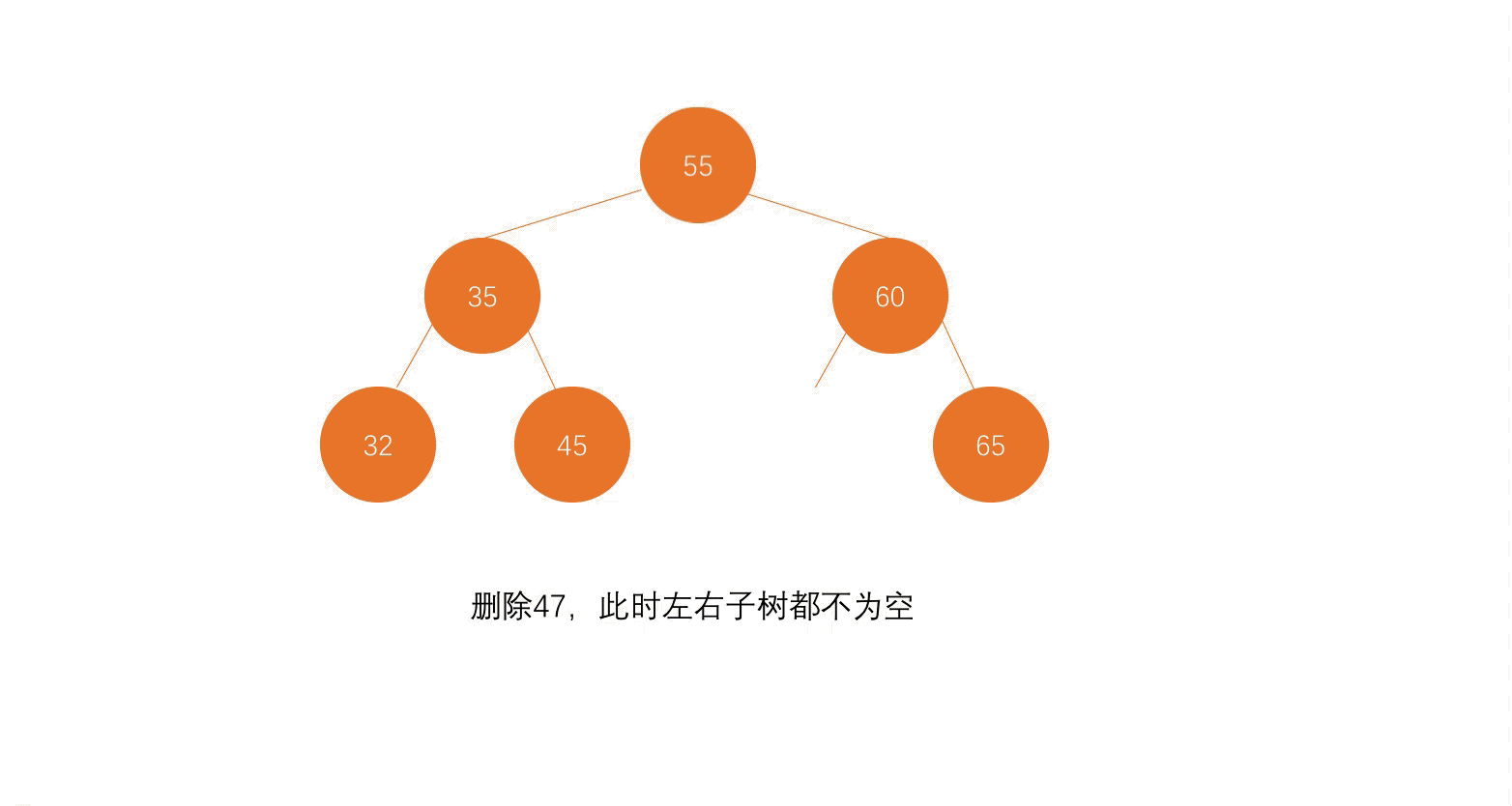
二叉树也是一种动态的数据结构。每个节点只有两个叉,也就是两个孩子节点,分别叫做左孩子,右孩子,而没有一个孩子的节点叫做叶子节点。每个节点最多有一个父亲节点,最多有两个孩子节点(也可以没有孩子节点或者只有一个孩子节点)。47左半边的所有节点组合起来形成了47的左子树,47右半边所有节点结合起来形成了47的右子树。如下图所示:
综合一下,涉及到的概念有:
根节点:二叉树的起始节点,唯一没有父亲节点的节点;
父亲节点:每个节点只有一个父亲节点。如上图47就是35的父亲节点;
左右孩子节点:每个节点至多拥有两个孩子节点,分别叫左孩子,右孩子;
左子树右子树:每个节点左边或者右边部分所有节点组合成的树结构。
1.2 二分搜索树
1.2.1 性质
第一,二分搜索树是一颗二叉树,满足二叉树的所有定义;
第二,二分搜索树每个节点的左子树的值都小于该节点的值,每个节点右子树的值都大于该节点的值。
第三,任意节点的每颗子树都满足二分搜索树的定义。
1.2.2 意义
当我们看到二分搜索树的定义时,是否会去联系这样定义的意义何在呢?其实,二分搜索树是在给数据做整理,因为左右子树的值和根节点存在大小关系,所以在查找元素时,我们于根节点进行对比后,就能每次近乎一半的去除掉查找范围,这就大大的加快了我们的查询速度,插入元素时也是一样。
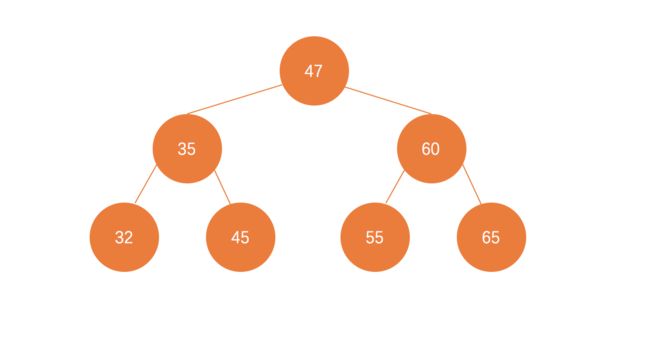
在图1-2中,如果要查找元素55,那么和根节点47对比后,发现55比47大,于是就往47右孩子60中去查询,接着发现55比60小,就往60左孩子中查询,于是就找到了这个元素。想象一下,如果是一个链表,那么将一个一个查询下去,速度可想而知。
其实在生活中,这样的例子也比比皆是,我们去超市买东西,超市也把一二三楼卖的是啥写的很清楚,假如三楼卖的是生鲜果蔬,而我们要买今天的菜,那么我们就直接去三楼,一楼和二楼我们就可以不用去找了,大大加快了我们选购商品的速度。图书馆找书也是这样的例子。所以二分搜索树的意义也就在此,很多时候数据结构其实来源于生活,于生活中解决实际问题,这就是技术的力量和价值的体现。
但是,为了达到这样的高效性,树结构由此也需要每个节点之间具备可比较性。而链表数据结构就没有这类要求,所以还是那句话,有得必有失。
到此我们就可以轻松定义出来二分搜索树的基本代码如下:
public class BST> {
private class Node {
public E e;
public Node left, right;
public Node(E e) {
this.e = e;
left = right = null;
}
}
private int size;
private Node root;
}
1.3 添加元素
我们一起来看看在一个树中插入元素的动画演示过程,如下图元素65插入树结构所示,元素在插入时,不断跟当前根节点进行对比,以来选择插入到左子树还是右子树。
通过动画,我们对树结构插入操作有了一个大致了解。现在我们来一步一步实现添加过程,将复杂问题简单化:
1.3.1 第一步
当前状态:无节点。
当然是从一棵空树开始,这个时候来一个元素,这时当然是赋值给root根节点。很自然,我们就想到如下代码:
public void add(E e) {
if (root == null) {
root = new Node(e);
size++;
} else {
}
}
1.3.2 第二步
当前状态:有节点,但节点左孩子或右孩子为空或左右孩子都为空。
这一步,我们已经有了根节点了,那么将在else中写逻辑。由下面动画我们知道,这时需要判断两个条件:
第一,插入元素与当前节点大小的比较;
第二,程序当前所在节点下左右节点是否为空,如果为空,那么就把添加的节点插入在这个位置上。
接下来,我们将用递归的方式进行元素的添加,我们先解决在某一节点上添加元素这个子问题。那么下面代码块中 add(root, e);这句代码把根节点传入,就是在根节点上添加元素,那么代码如下:
public void add(E e) {
if (root == null) {
root = new Node(e);
size++;
} else {
add(root, e);
}
}
// 在node为根节点的树中,添加元素e
private void add(Node node, E e) {
if (node.e.compareTo(e) == 0) {
return;
}
// 添加到左孩子的位置,
// 条件:添加的元素小于node节点的元素,node节点的元素的左孩子为空
if (e.compareTo(node.e) < 0 && node.left == null) {
node.left = new Node(e);
size++;
return;
}
// 添加到右孩子的位置
if (e.compareTo(node.e) > 0 && node.right == null) {
node.right = new Node(e);
size++;
return;
}
}
1.3.3 第三步
当前状态:有节点,左右孩子都不为空。
如果当前节点左右孩子都不为空,那么就递归的把当前节点的左孩子或右孩子传递进add方法。如下:
public void add(E e) {
if (root == null) {
root = new Node(e);
size++;
} else {
add(root, e);
}
}
private void add(Node node, E e) {
if (node.e.compareTo(e) == 0) {
return;
}
if (e.compareTo(node.e) < 0 && node.left == null) {
node.left = new Node(e);
size++;
return;
}
if (e.compareTo(node.e) > 0 && node.right == null) {
node.right = new Node(e);
size++;
return;
}
// 递归调用,如果当前节点左右节点不为空,则进入下一轮递归的调用。
if (e.compareTo(node.e) < 0) {
add(node.left, e);
} else {
add(node.right, e);
}
}
换一种思考方式
我们如果仔细观察上面的逻辑就会发现,只要添加元素,那么这个位置肯定是空节点,用递归的话,我们的循环终止条件就可以用当前位置是否为空来判断,代码瞬间简单了许多,如下:
public void add(E e) {
root = addAnother(root, e);
}
// 返回插入新节点后,二分搜索树的根
private Node addAnother(Node node, E e) {
if (node == null) {
size++;
return new Node(e);
}
if (e.compareTo(node.e) < 0) {
node.left = addAnother(node.left, e);
} else if (e.compareTo(node.e) > 0) {
node.right = addAnother(node.right, e);
}
return node;
}
1.4 树的遍历
树的遍历分为前序遍历,中序遍历,后序遍历,层序遍历。我们依次来讲一讲。
1.4.1 前序遍历
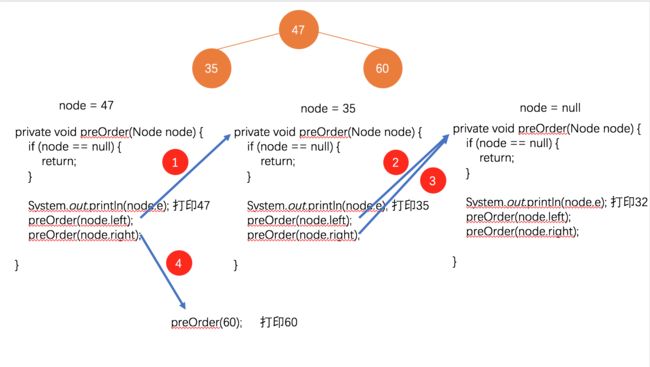
前序遍历,就是我们在递归调用前,先做我们的逻辑(这里的逻辑就是打印一下当前元素),前序遍历代码如下:
private void preOrder(Node node) {
if (node == null) {
return;
}
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
我们以一个节点为例子,如节点后还有节点,递归会循环处理。以下树结构最终打印的结果就是47,35,60。
1.4.2 中序遍历与后续遍历
那么接下来就是中序遍历,中序遍历就是把对元素的操作操作放在了中间,先不断递归左孩子,然后对元素进行操作,最后递归右孩子。所以很容易的推理出来,中序遍历是对元素从小到大的排序遍历。这个性质可以作为判断二分搜索树的一个条件。
同理可以推出还有后续遍历,这里就不再赘述了。
1.4.3 层序遍历
最后我们一起来聊聊层序遍历,顾名思义,层序遍历就是对树结构一层一层的遍历。要做到这一点,我们可以很方便的想到利用队列来实现这一过程。我们每次从队列中取出一个元素时,接着就把该元素的左右两孩子推入队列中,然后依次取出元素,以此来做到按层把元素遍历一遍。
一起来看看动画爸爸给我们的演示,最直观。
由动画爸爸很容易看出,依次打印的顺序分别为:47,35,60,32,45,55,65,完美完成层序遍历。
然后我来奉上代码妈妈:
public void levelOrder() {
Queue q = new LinkedList<>();
// 把根节点放入队列
q.add(root);
while (!q.isEmpty()) {
// 移除并返回队列中的第一个节点
Node front = q.remove();
System.out.print(front.e + " ");
// 把移除元素的左右孩子推出队列
if (front.left != null) {
q.add(front.left);
}
if (front.right != null) {
q.add(front.right);
}
}
}
1.5 删除元素
1.5.1 后继节点
接下来,我们聊聊元素的删除。在此之前,我们先得引入一个概念,元素的前驱或者后继节点。
后继节点:一个节点右子树中,最小的节点为该节点的后继节点。后继节点是比该节点所有大的元素中最小的元素。
之所以要引入这个概念,原因是在删除元素时,我们需要找一个元素替代被删除位置的元素,但是由于二分搜索树的特性,不能随便找元素过来代替,必须得找一个和被删除元素最接近的元素来替代其位置。所以找前驱或后继替代都可以。
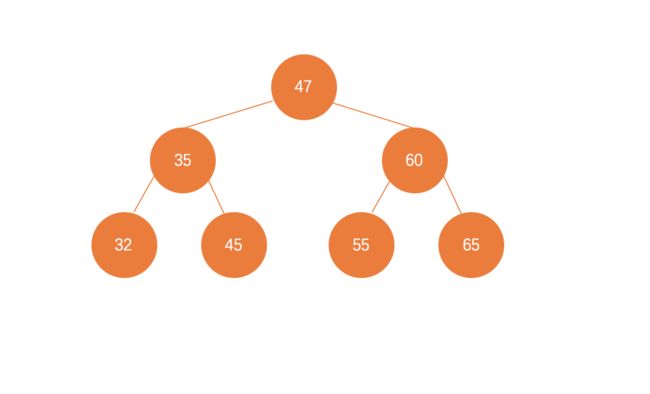
比如说,如下图,47的后继节点就是55,右子树中最小的元素。
1.5.2 删除元素的过程
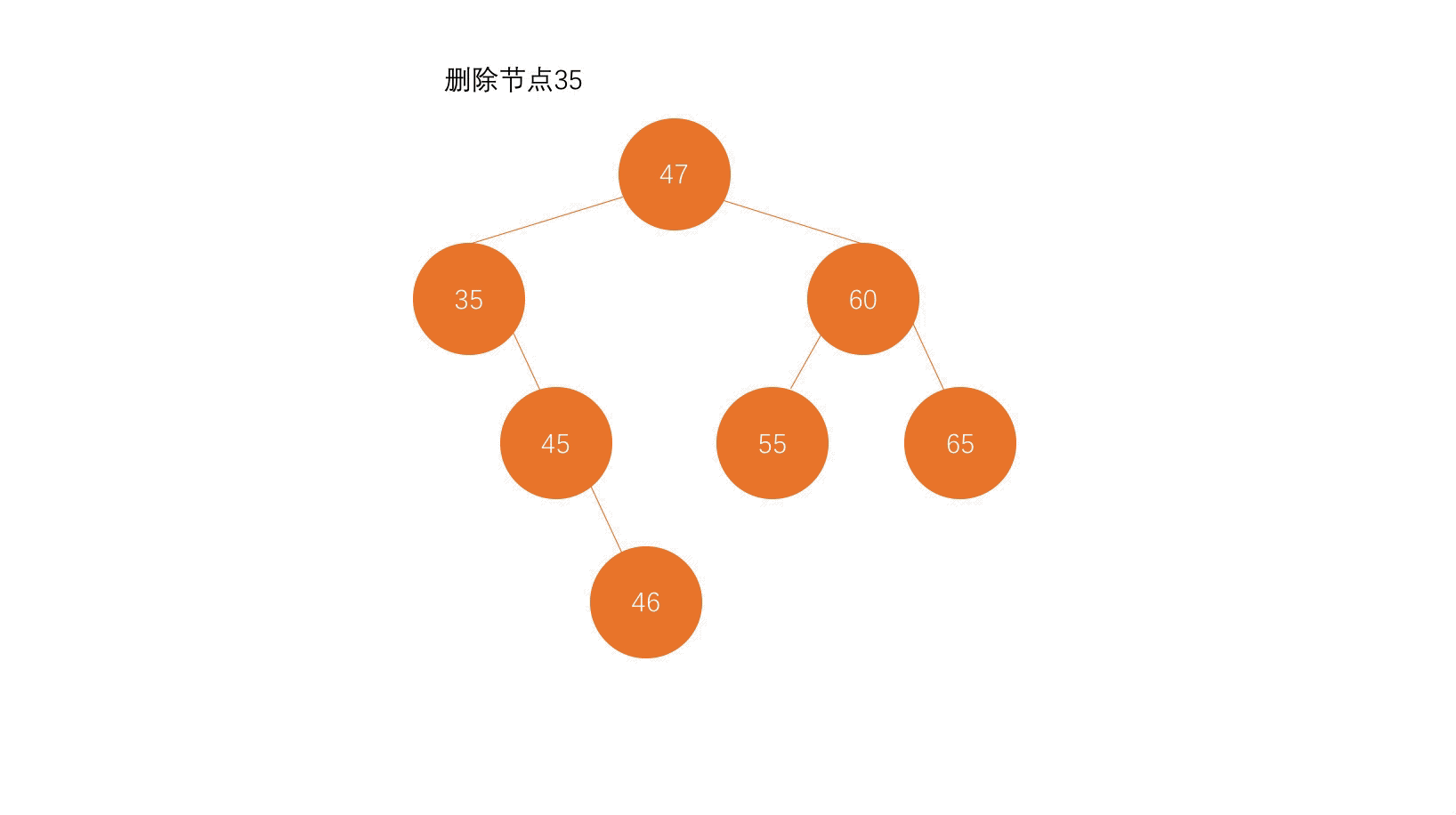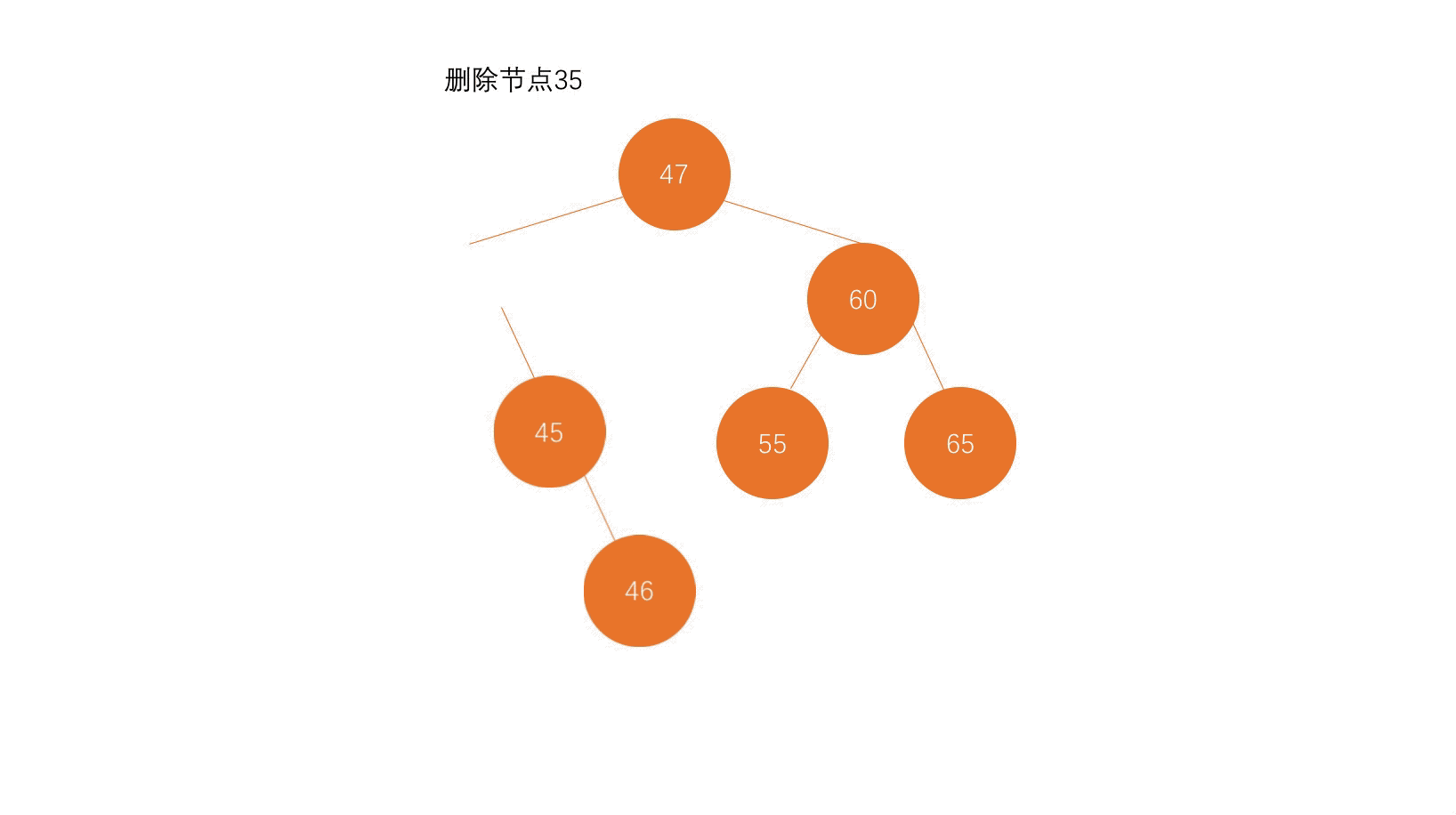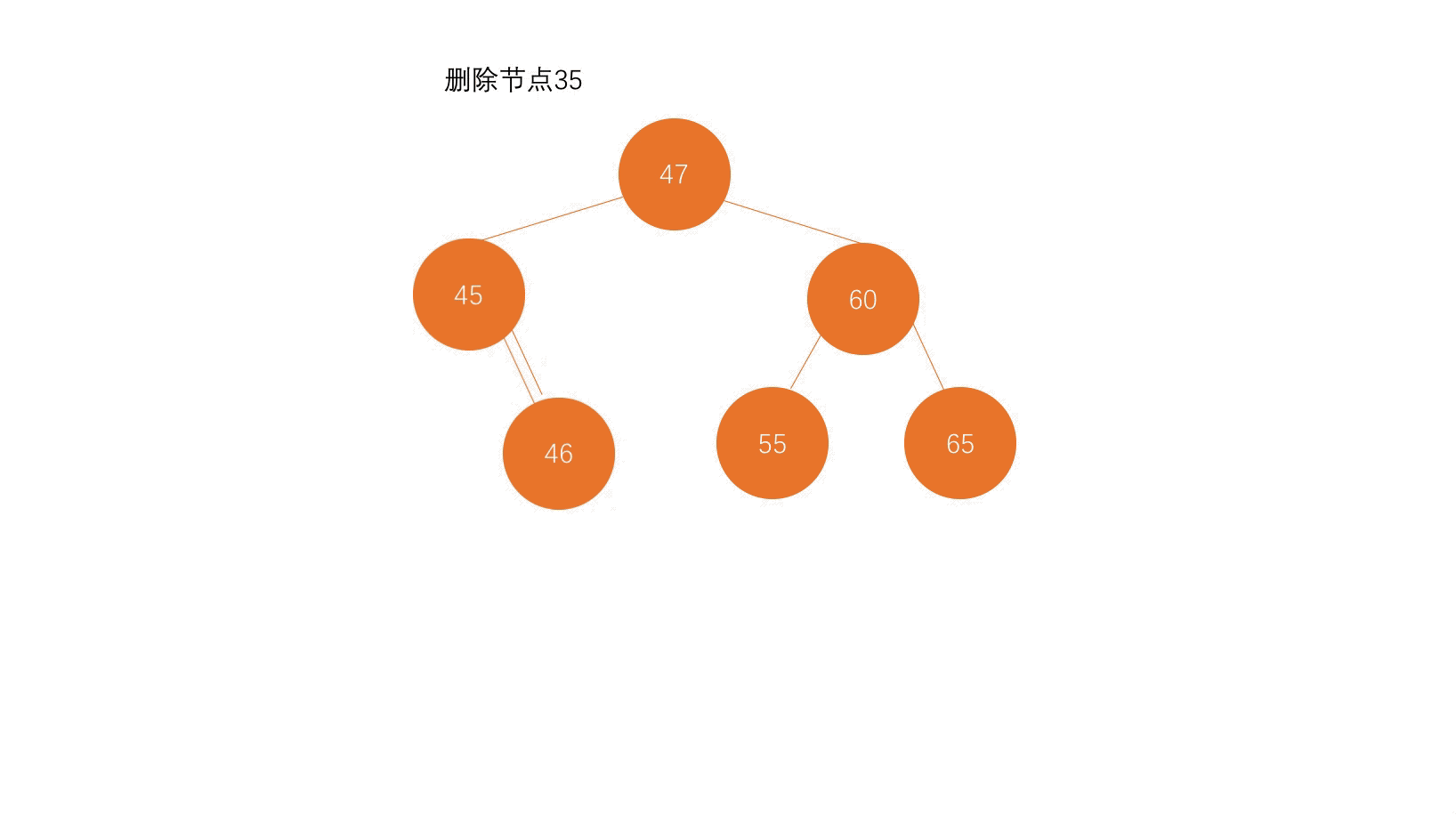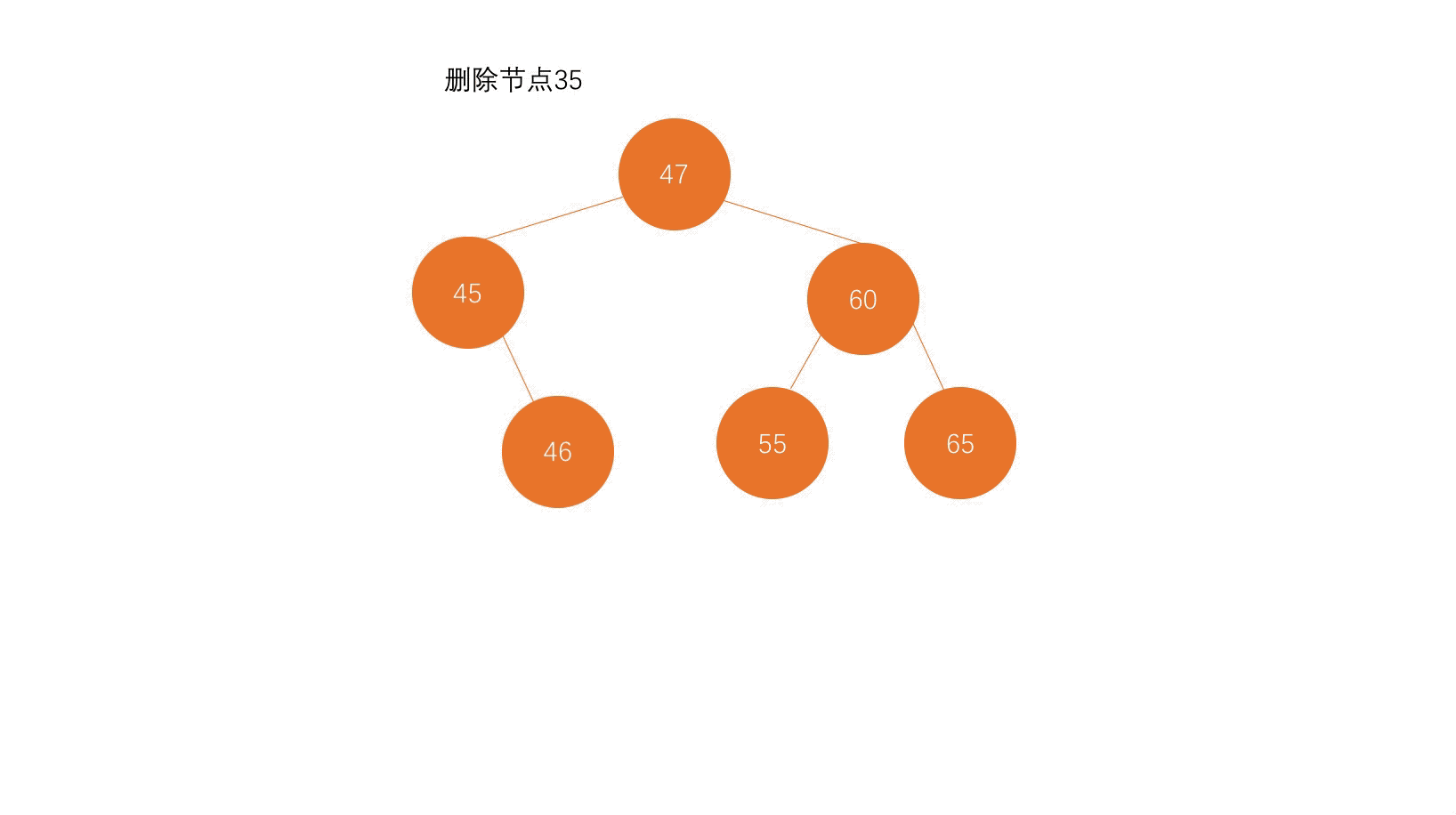
我们分情况讨论,待删除元素可能有以下三种情形。
第一种,只有左孩子;
第二种,只有右孩子;
第三种,左右孩子都有;(当然还有一种情况就是为叶子节点,那么直接删除即可)
同理很容易就能推出右子树为空时的删除过程。
接下来我们来看看左右子树不为空的情况。这种情况动画演示比较简单,我们看看整体的过程。
第一步,找到待删除元素;
第二步,找到待删除元素的后继节点;
第三步,把待删除元素的左子树赋值给后继节点的左子树,把待删除元素的右子树最小元素删除后,赋值给后继节点的右子树。
整体代码如下:
public void remove(E e) {
root = remove(root, e);
}
private Node remove(Node node, E e) {
if (node == null) {
return null;
}
if (e.compareTo(node.e) < 0) {
node.left = remove(node.left, e);
return node;
} else if (e.compareTo(node.e) > 0) {
node.right = remove(node.right, e);
return node;
} else { // 找到了待删除元素
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
if (node.right == null) {
Node leftNode = node.left;
node.left = null;
size--;
return leftNode;
}
// 后继节点
Node successor = minimum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
return successor;
}
}