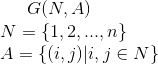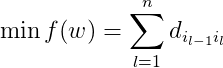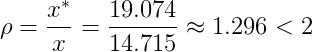本章涉及知识点
1、NP完全问题和其解题策略
2、TSP问题定义
3、案例引出
4、满足三角不等式的TSP模型
5、近似算法的解题步骤
6、图的存储结构
7、Prim最小生成树算法
8、树的遍历方法
9、哈密顿回路
10、python编程实现近似算法
11、结果分析
一、NP完全问题和其解题策略
一般的,我们将可以在多项式时间之内可求解的问题定义为易处理问题,而将需要超多项式时间才能求解的问题定义为难处理问题
对于一个规模为n的输入,在最坏的情况下(穷举法)求解的时间复杂度为
其中k是某个确定的常数,我们将这类问题定义为P类问题,直观上,P类问题是在确定性计算模型下的易解问题类
而NP问题就是在非确定性计算模型下的难处理问题
至今为止,人类还没有找到NP完全问题的多项式时间算法,并且没有人可以证明NP问题不存在多项式时间算法,这也成为了理论计算机科学领域中最深奥的开放问题之一,也是NP完全问题令人惊奇的性质
21世纪至今,人类对于任何一个NP完全问题,还没有多项式时间算法,因此,在面对NP问题时,通常有以下几种解题的策略
(1)只针对NP问题的特殊实例求解
(2)动态规划或者分支限界法
(3)概率论算法
(4)近似解法
(5)人工智能启发式算法
(6)神经网络算法
可以看到,无论使用什么上述策略解题,我们只能无限逼近其最优解,而不能保证得到通解,本章我们将使用近似解法来求解NP完全问题
二、TSP问题定义
旅行商问题(Traveling salesman problem),简称为TSP问题,是1959年提出的数学规划问题,TSP属于典型的NP完全问题
TSP问题的语言描述为
在一个具有n个城市的完全图中,旅行者希望进行一次巡回旅行,或经历一次哈密顿回路,可以恰好访问每一个城市一次,并且最终回到出发城市。而这次巡回旅行的总费用为访问各个城市费用的总和,故旅行者同时希望整个行程的费用是最低的,求这个路线的排列策略?
TSP问题的实质可以抽象为
在一个带权重的完全无向图中,找到一个权值总和最小的哈密顿回路
TSP问题翻译为数学语言为,在N个城市的完全无向图G中
其中每个城市之间的距离矩阵为
目标函数为
需要求解的变量为w,w是使得目标函数达到最小值的一个排列
且w的最后一项满足回到出发城市
显然,TSP问题的组合解有N!种组合,随着城市数量N的规模增加,组合数将呈指数级别递增,故使用穷举法将会面临组合爆炸问题,因此TSP属于NP完全问题
三、案例引出
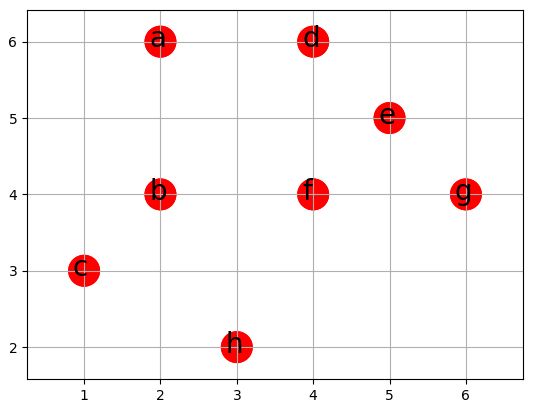
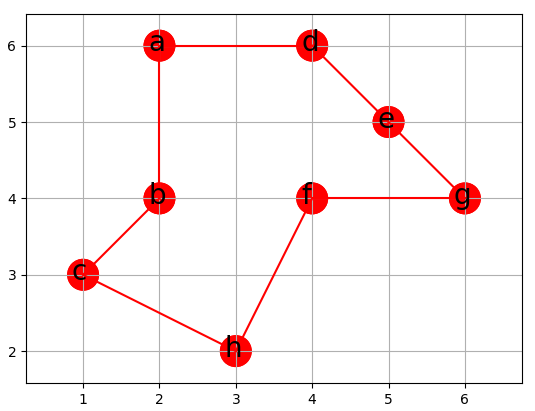
有如下含有8个顶点的完全无向图G,每一边有非负的费用值,试着找出G的最小费用的哈密顿回路?
其中各个城市的坐标为
这个案例的组合数为8!=40320种组合
四、满足三角不等式的TSP模型和算法步骤
接下来,我们选择近似算法来求解案例TSP问题
我们从费用函数出发,费用函数也叫代价函数,指的是两个城市之间的费用指数或者代价程度的量化。在大多数的实际情况中,从一个地方u直接到另一个地方w,这个走法花费的代价总是最小的,而如果从u到w需要经过某个中转站v,则这种走法花费的代价却不可能比直接到达的走法花费的代价更小
将上述的理论转化为数学语言为
其中c是费用函数,这个方程说明了,直接从u->w花费的代价,要比从u->v->w花费的代价要小,我们称这个费用函数满足三角不等式
三角不等式的定义为:任意一个欧拉平面的三角形两边之和始终大于第三边,这是一个非常自然的不等式,其中欧拉平面上任意两点之间的欧式距离就满足三角不等式,
为此,我们只要设TSP中的费用函数为欧式距离,即可将TSP问题转化为满足三角不等式的TSP模型
五、近似算法的解题步骤
求解上述TSP模型的近似算法分为以下步骤
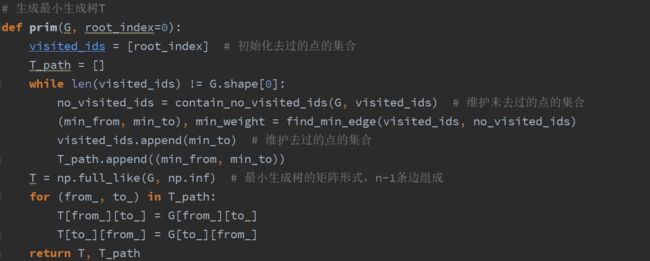
(1)选择G的任意一个顶点r作为根节点(出发/结束点)
(2)用Prim算法找出G的一棵以r为根的最小生成树T
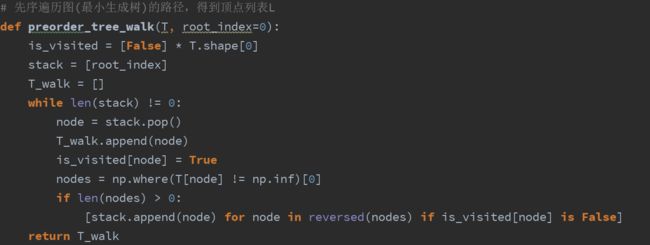
(3)前序遍历访问树T,得到遍历顺序组成的顶点表L
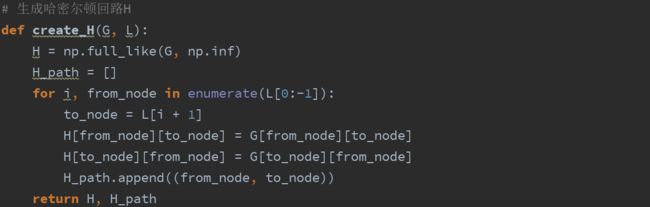
(4)将r加到顶点表L的末尾,按L中顶点的次序组成哈密顿回路H
数学上已经证明,当费用函数满足三角不等式时,上述近似算法找出的哈密顿回路产生的总费用,不会超过最优回路的2倍
下面我们就按照近似算法的步骤来一步步求解案例TSP问题
六、图的存储结构
首先我们需要将图表示为我们熟悉的数据结构,图可以使用两种存储结构,分别是邻接链表和邻接矩阵
邻接链表:是一个由链表组成的一维数组,数组中每个元素都存储以每个顶点为表头的链表
邻接矩阵:以矩阵的形式存储图中所有顶点之间的关系
用链表表示图的关系,会显得数据结构较为复杂,但节省空间的开销,而用矩阵来表示图的关系就显得非常清晰,但空间开销较大,这里我们选择邻接矩阵来表示TSP案例中的无向图G
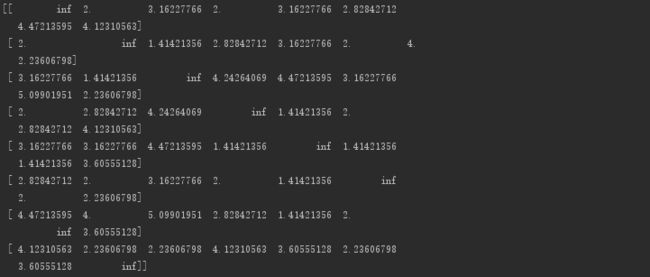
我们设欧式距离为费用函数,矩阵中的每一行代表G中每一个的顶点到其余各个顶点的费用(欧式距离),如果出现到达不了或者自身到达自身的情况,我们用无穷大inf来填充表示不可达
至此,我们就定义好了G的存储结构,就可以很清晰的访问翻译G的每一个数据,如G[2][3]就翻译为:从第2个城市到达第3个城市的费用为4.24264096
至此,我们就完成近似算法的第一步
七、Prim最小生成树算法
我们知道,两点可以确定一条直线,则最小生成树的定义为:用n-1条边连接具有n个顶点的无向图G,并且使得边长的总和最小
接下来我们需要找到G中的这颗最小生成树T,从T的定义可知,T满足
(1)T有且只有n-1条边
(2)T的总长度达到最小值
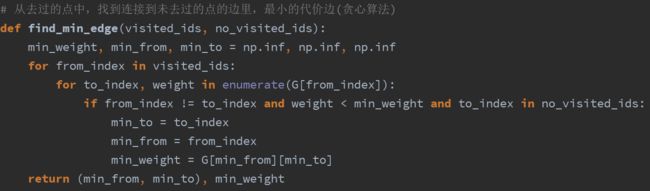
这里我们使用Prim算法来生成T,Prim算法的策略步骤为
(1)设集合V是G中所有的顶点,集合U是G中已经走过的顶点,集合U-V是G中没有走过的顶点
(2)从G中的起点a开始遍历,将a加入到集合U中,并将a从集合U-V替出
(3)在集合U-V中剩余的n-1个顶点中寻找与集合U中的a关联,且权重最小的那条边的终点b,将b加入到集合U中,并将b从集合U-V替出
(4)同理,在集合U-V中剩余的n-2个顶点中寻找与集合U中的a或b关联,且权重最小的那条边的终点c,将c加入到集合U中,并将c从集合U-V替出
(5)重复步骤(4),直到G中所有的顶点都加入到集合U,且集合U-V为空,则集合U中的顶点就构成了T
显然,Prim算法的策略属于贪心算法,因为每一步所加入的边,都必须是使得当前数T的总权重增加量最小的边
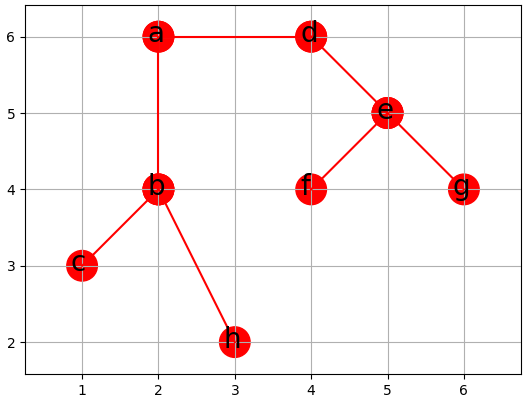
按照Prim算法,我们案例的最小生成树T为
至此,我们就完成近似算法的第二步
八、树的遍历方法
找到T之后,接下来需要遍历T,我们知道,遍历一棵树有三种遍历规则,前序遍历、中序遍历和后序遍历
(1)前序遍历:访问根节点—>前序遍历左子树—>前序遍历右子树
(2)中序遍历:前序遍历左子树—>访问根节点—>前序遍历右子树
(3)后序遍历:前序遍历左子树—>前序遍历右子树—>访问根节点
上述案例中的T,以a为根节点开始前序遍历,遍历出的节点即组成顶点表L
至此,我们就完成近似算法的第三步
九、哈密顿回路
哈密顿回路的定义为:由指定的起点前往指定的终点,途中经过的城市有且只经过一次,所以一个无向图中含有若干个哈密顿回路
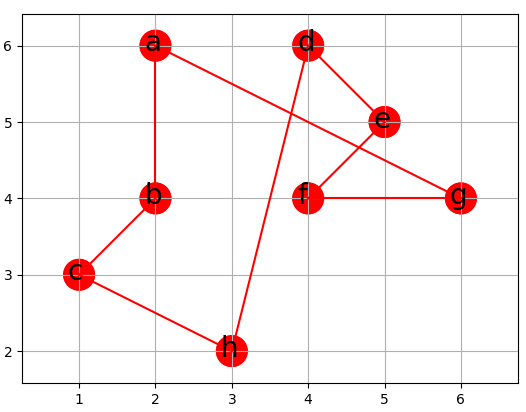
按照近似算法的最后一步,我们将T的根节点a加入到顶点表L的末尾,将L的顶点顺序依次连接,就得到T的哈密顿回路H
至此,我们就完成了近似算法的计算,找到了一个在G中从a出发,最后回到a,中间每个城市只经过一次的最小费用的行程走法,即计算出了目标函数的顶点排列w为
按照这个排列,旅行线路的总费用x*=19.074
十、python编程实现近似算法
接下来我们将近似算法翻译为代码即可
十一、结果分析
从结果上可以看出,近似算法是解决TSP问题的一种有效方法,它可以在多项式时间内计算出一个近似解,来逼近真实的最优解,这个近似解尽量的逼近满足TSP的条件
(1)从开始点回到开始点,每个点都要经过且只经过一次
(2)行程的总费用达到最小值
案例中,实际的最优解(顶点组合)应该是
实际的最优解的总费用为x=14.715
我们可以看到,近似算法找出的近似解的总费用x*,和实际最优解的总费用x满足比例
我们可以总结出以下几点近似算法求解TSP问题
(1)近似算法是求解TSP问题的一个渐进式算法
(2)近似解法求出的近似解和实际最优解的近似比不超过2,即w的总代价,在最优总代价的2倍之内
最后,要想真正的计算出案例的最优解,我们需要求解TSP问题的另一种算法—人工智能启发式算法,这个算法我们在下一讲中再来说明
案例代码见:求解TSP问题—近似算法