不要使用暴力的方法,可以学学讨论里的技巧
二维数组中的查找
题目:在一个二维数组中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
想法1:C++语言都忘了,百度了vector
代码1:
class Solution {
public:
bool Find(int target, vector > array) {
for(int i = 0;i 结果1:段错误:您的程序发生段错误,可能是数组越界,堆栈溢出(比如,递归调用层数太多)等情况引起
case通过率为0.00%。
想法2:使用二分查找方法,序号(0,1,2,3,4····)和坐标([0,0],[0,1]````)可以按这样转换。因为行列相同Y,所以X=[X/Y,X%Y]。
看了下python的实现:
def bin_search(data_list, val):
low = 0 # 最小数下标
high = len(data_list) - 1 # 最大数下标
while low <= high:
mid = (low + high) // 2 # 中间数下标
if data_list[mid] == val: # 如果中间数下标等于val, 返回
return mid
elif data_list[mid] > val: # 如果val在中间数左边, 移动high下标
high = mid - 1
else: # 如果val在中间数右边, 移动low下标
low = mid + 1
return # val不存在, 返回None
ret = bin_search(list(range(1, 10)), 3)
print(ret)
代码2:
class Solution {
public:
bool Find(int target, vector > array) {
int min = 0;
int max = array.size() * array.size() - 1;
while(min <= max){
int mid = (min + max) / 2;
if(target == array[mid / array.size()][mid % array.size()]){
return true;
}
if(target > array[mid / array.size()][mid % array.size()]){
min = mid + 1;
}
else{
max = mid - 1;
}
}
return false;
}
};
结果2:您的代码已保存
段错误:您的程序发生段错误,可能是数组越界,堆栈溢出(比如,递归调用层数太多)等情况引起
case通过率为0.00%
思考3:原来每个一维数组的长度相同的意思不是行列相同0.0,是每一行的长度相同。上面的想法都错了0.0。使用遍历的办法试试。
代码3:
class Solution {
public:
bool Find(int target, vector > array) {
for(int i = 0;i < array.size();i++){
for(int j = 0;j < array[0].size();j++){
if(target == array[i][j]){
return true;
}
}
}
return false;
}
};
结果3:您的代码已保存
答案正确:恭喜!您提交的程序通过了所有的测试用例。
思考4:看看我的二分法行不行。使用二分查找方法,序号(0,1,2,3,4····)和坐标([0,0],[0,1]````)可以按这样转换。因为列数=Y,所以X=[X/Y,X%Y]。
代码4:
class Solution {
public:
bool Find(int target, vector > array) {
int min = 0;
int max = array.size() * array[0].size() - 1;
while(min <= max){
int mid = (min + max) / 2;
if(target == array[mid / array[0].size()][mid % array[0].size()]){
return true;
}
if(target > array[mid / array[0].size()][mid % array[0].size()]){
min = mid + 1;
}
else{
max = mid - 1;
}
}
return false;
}
};
结果4:
您的代码已保存
答案错误:您提交的程序没有通过所有的测试用例
case通过率为0.00%
用例:
7,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]
对应输出应该为:
true
你的输出为:
false
分析:不是严格递增。
总结:题目需要分析清楚。看了下别人的思路,可以按每行来二分,每行是严格递增的。还有按数字的特性,从左下角开始查找,查找的元素较小,往上找;查找元素较大,往右找。
替换空格
题目:请实现一个函数,将一个字符串中的每个空格替换成“%20”。例如,当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。
思考1:
从前往后修改,会覆盖掉原有的记录?从后往前修改,先查找出空格数目,然后找出规律,修改后的字符位置从原来的[i]--->[i+num*2]。
代码1:
void replaceSpace(char *str,int length) {
int num = 0 ;
for(int i =0;i= 0; i--){
if(str[i] != ' '){
str[i+num*2] = str[i];
}
else{
str[i+num*2] = '0';
str[i+num*2-1] = '2';
str[i+num*2-2] = '%';
num--;
}
}
}
结果1:
您的代码已保存
答案正确:恭喜!您提交的程序通过了所有的测试用例
从尾到头打印链表
题目:输入一个链表,按链表值从尾到头的顺序返回一个ArrayList。
思考1:vector就是一个动态数组。链表从头到尾遍历加入数值到vector,然后从尾到头遍历vector。
代码1:
vector printListFromTailToHead(ListNode* head) {
vector a;
vector b;
while(head != NULL){
a.push_back(head->val);
head = head->next;
}
for(int i = a.size()-1; i >=0;i--){
b.push_back(a[i]);
}
return b;
}
结果1:
您的代码已保存
答案正确:恭喜!您提交的程序通过了所有的测试用例
重建二叉树
题目:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
思考:前序遍历中找出根节点,在中序遍历中根据找到的根节点区分左右子树集。递归思想。但是不会写,参考下别人的讨论。递归返回左右子树的根节点。
代码1:
TreeNode* reConstructBinaryTree(vector pre,vector vin) {
if(vin.size()==0||pre.size()==0){
return NULL;
}
int vin_index;
for(int i = 0 ; i < vin.size();i++){
if(pre[0] == vin[i]){
vin_index = i;
break;
}
}
vector vin_left(vin.begin(),vin.begin()+vin_index);
vector vin_right(vin.begin()+vin_index+1,vin.end());
vector pre_left(pre.begin()+1,pre.begin()+vin_left.size()+1);
vector pre_right(pre.begin()+vin_left.size()+1,pre.end());
TreeNode *root = new TreeNode(pre[0]);
root->left = reConstructBinaryTree(pre_left,vin_left);
root->right = reConstructBinaryTree(pre_right,vin_right);
return root;
}
结果1:通过,注意vector复制的区间是左闭右开的,而且end()指向的时最后一个元素的后面一个虚拟元素,所以你想把*a = [0,1,2,3]复制给vector的时候得vector b(a,a+4)而不是vector b(a,a+4-1)。
用两个栈实现队列
题目:用两个栈来实现一个队列,完成队列的Push和Pop操作。 队列中的元素为int类型。
思考1:
一个用来收集进入的数s1,一个用来释放的数s2,如果s2空了的话,把s1的数目导入进s2。
代码1:
class Solution
{
public:
void push(int node) {
stack1.push(node);
}
int pop() {
int a;
if(stack2.size()== 0){
while(!stack1.empty()){
stack2.push(stack1.top());
stack1.pop();
}
}
a=stack2.top();
stack2.pop();
return a;
}
private:
stack stack1;
stack stack2;
};
结果1:通过,注意别忘记using namespace std;,还有C++种初始变量可以不用new,new是自己申请内存,得释放,而且是针对指针?
旋转数组的最小数字
题目:把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。 输入一个非减排序的数组的一个旋转,输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转,该数组的最小值为1。 NOTE:给出的所有元素都大于0,若数组大小为0,请返回0。
思考1:非减排序的数组。那么就是不是严格增加的数组?。那么最小的在第一个,旋转后,如果出现了降序,那么第一个就是最小值?
代码1:
int minNumberInRotateArray(vector rotateArray) {
if(rotateArray.size()==0){
return 0;
}else{
for(int i = 0; i 结果1:通过,考虑清楚3种情况,第一种是0大小,第二种是正常,第三种是{1,1,1,1}。
斐波那契数列
题目:大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。
n<=39
思考1:一看到这个题目就想到递归。
代码1:
int Fibonacci(int n) {
if(n==0){
return 0;
}
if(n==1){
return 1;
}
return Fibonacci(n-1)+Fibonacci(n-2);
}
结果1:
运行超时:您的程序未能在规定时间内运行结束,请检查是否循环有错或算法复杂度过大。
思考2:优化?从前往后算,n-1表示算的次数跳过n=0,n=1。使用vector保存计算的结果,用于调用。
代码2:
int Fibonacci(int n) {
if(n <= 1){return n;}
vector a;
a.push_back(0);
a.push_back(1);
int temp;
for(int i = 0; i < n-1 ; i++){
temp = a[i] +a[i+1];
a.push_back(temp);
}
return *(a.end()-1);
}
结果2:通过,使用保存结果优化。
跳台阶
题目:一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法(先后次序不同算不同的结果)。
思考1:按2的数目,排列组合
代码1:
int jumpFloor(int number) {
int n = number/2;
int sum = 0;
for(int i = 0 ; i <= n ;i++){
int all = number - i*2+i;
int temp = 1;
int temp2 = 1;
for(int j = all ; j> all-i ; j--){
temp = temp * j ;
}
for(int m = 1 ; m<= i ; m++){
temp2 = temp2 *m;
}
if(i == 0){
sum += 1;
}else{
sum += (temp/temp2);
}
}
return sum;
}
结果1:
不通过
您的代码已保存
答案错误:您提交的程序没有通过所有的测试用例
case通过率为47.37%
用例:
29
对应输出应该为:
832040
你的输出为:
322365
思考2:感觉想法没错,那么看看结果,在计算29中出现了负数。想到超出了int的范围,改为double。
代码2:
int n = number/2;
int sum = 0;
for(int i = 0 ; i <= n ;i++){
int all = number - i*2+i;
double temp = 1;
double temp2 = 1;
for(int j = all ; j> all-i ; j--){
temp = temp * j ;
}
for(int m = 1 ; m<= i ; m++){
temp2 = temp2 *m;
}
if(i == 0){
sum += 1;
}else{
sum += (temp/temp2);
}
}
return sum;
结果2:通过,以后注意数据超出范围的问题。
变态跳台阶
题目:一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
思考1:手写了几个答案后发现规律。(2)=2,(3)=4,(4)=8,(5)=16。(n)=2^(n-1)。
代码1:
int jumpFloorII(int number) {
if(number == 0) return 0;
if(number == 1) return 1;
int sum = 1;
for(int i = 1;i结果1:通过,但是看评论好像是考验递归思想。
思考2:用递归思想。f(n)=f(n-1)+f(n-2)+f(n-3).......+f(n-n)。后面是第一次跳1到N台阶后的选择。
代码2:
int jumpFloorII(int number) {
if(number == 0) return 1;
int sum = 0;
for(int j = 1 ; j <= number ; j++){
sum += jumpFloorII(number-j);
}
return sum;
}
矩形覆盖
题目:我们可以用21的小矩形横着或者竖着去覆盖更大的矩形。请问用n个21的小矩形无重叠地覆盖一个2*n的大矩形,总共有多少种方法?
思考1:和之前的跳台阶一样,长n可以选择2或者1.
代码1:
int n = number/2;
int sum = 0;
for(int i = 0 ; i <= n ;i++){
int all = number - i*2+i;
double temp = 1;
double temp2 = 1;
for(int j = all ; j> all-i ; j--){
temp = temp * j ;
}
for(int m = 1 ; m<= i ; m++){
temp2 = temp2 *m;
}
if(i == 0){
sum += 1;
}else{
sum += (temp/temp2);
}
}
return sum;
}
结果1:
用例:
0
对应输出应该为:
0
你的输出为:
1
结论1:没考虑0 。在一开始加入0的情况返回0后通过。以后要注意0的情况。
思考2:看了下别人的代码,发现可以跟变态台阶一样,就是选择横放或者竖放。
代码2:
if(number < 0 ) return 0;
if(number == 1) return 1;
if(number == 2 ) return 2 ;
int sum = 0;
sum = rectCover(number -1) + rectCover(number -2);
return sum;
二进制中1的个数
题目:输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。
思考1:正数可以用除法算出有多少个1,负数先去掉符号变成补码,再算多少个1?考虑int是32位。
参考了下讨论里的代码:n & 0x7fffffff。这个技巧把负数的符号去掉了,变成了正数,好像不是正数,而是去掉符号位的补码。
代码1:
int NumberOf1(int n) {
int all = 0;
if(n<0) {all++; n = n & 0x7fffffff;}
while(n!=0){
int a;
a = n/2;
if(n%2==1) all++;
n=a;
}
return all;
}
结果:通过。对位运算不太熟悉,需要加强。
数值的整数次方
题目:给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。
思考1:按次方和0的比较计算。
代码1:
double r = 1;
int n ;
if(exponent == 0 ) return 1;
n = abs(exponent);
for(int i = 0 ;i 0 ) return r;
if(exponent < 0) return 1/r;
return 0;
结论:通过,最后个返回0是多余的,但是不加的话编译错误,好像因为return的都在条件下执行。
调整数组顺序使奇数位于偶数前面
题目:输入一个整数数组,实现一个函数来调整该数组中数字的顺序,使得所有的奇数位于数组的前半部分,所有的偶数位于数组的后半部分,并保证奇数和奇数,偶数和偶数之间的相对位置不变。
思考1:一个数组存奇数,一个数组存偶数,分别遍历赋值。
代码1:
vector list2 ;
vector list3 ;
for(int i = 0 ; i 结果1:通过,但是感觉太简单了,去看看有没有更好的办法。
他人1:
for(int i = 0;ii ;j--){
if (array[j]%2 == 1 && array[j-1]%2==0){
swap(array[j],array[j-1]);
}
}
}
我2:
//从前往后,冒泡。
//冒泡排序算法的原理如下:
//1.比较相邻的元素。如果第一个比第二个大,就交换他们两个。
//2.对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
//3.针对所有的元素重复以上的步骤,除了最后一个。
//4.持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
for(int i = 0;i链表中倒数第k个结点
题目:输入一个链表,输出该链表中倒数第k个结点。
思考1:先找出链表长度,然后减去K值,从头到尾遍历length-K。
代码1:
ListNode* FindKthToTail(ListNode* pListHead, unsigned int k) {
ListNode *head = pListHead;
int length = 1;
while(pListHead->next!=NULL){
length++;
pListHead = pListHead->next;
}
//cout<length){
return NULL;
}
for(int i = 0 ; inext;
}
return head;
}
结果1:
段错误:您的程序发生段错误,可能是数组越界,堆栈溢出(比如,递归调用层数太多)等情况引起
case通过率为0.00%
思考2:从讨论中发现弄两个指针一个先走K步,另一个从头开始走,最后指针1走到尾巴的时候,指针2走到了目标点。
代码2:
ListNode* FindKthToTail(ListNode* pListHead, unsigned int k) {
if(pListHead==NULL||k<=0){
return NULL;
}
ListNode *head = pListHead;
ListNode *result = pListHead;
int i = 0;
while(inext;
i++;
}
while(head != NULL){
head = head->next;
result = result->next;
}
return result;
}
结果2:通过,注意如果K太大记得返回NULL。
反转链表
题目:输入一个链表,反转链表后,输出新链表的表头。
思考1:一开始想弄冒泡排序的方法一个个换过来,但是弄不出来,然后借鉴下讨论里的想法,弄两个指针,然后自己按过程一个个交换过来,把交换过程转成代码。
注意返回的值应该是指针,不能是常量的地址。鲁棒性就是判断下一些异常情况。
代码1:
ListNode* ReverseList(ListNode* pHead) {
ListNode *p = NULL;
ListNode *c = NULL;
if(pHead == NULL) return NULL;
while(pHead!=NULL){
c = pHead;
pHead = pHead->next;
c->next = p;
p = c;
}
return c;
}
结果1:
通过了。不能直接抄代码,可以看一点思路,然后自己想想,画下流程,转成代码。
合并两个排序的链表
题目1:输入两个单调递增的链表,输出两个链表合成后的链表,当然我们需要合成后的链表满足单调不减规则。
思考1:两个头指针比较大小,然后加入新链表。注意判断所有情况(!N,!N),(!N,N),(N,!N),(N,N)。
代码1:
ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
{
ListNode* n ;
int i = 0;
ListNode* start = NULL;
if(pHead1 == NULL && pHead2 == NULL) return NULL;
while(pHead1 != NULL || pHead2 != NULL){
if(pHead1 != NULL && pHead2 != NULL){
if(pHead1->val < pHead2->val){
n->next = pHead1;
pHead1 = pHead1->next;
}else{
n->next = pHead2;
pHead2 = pHead2->next;
}
n=n->next;
}else if(pHead1 != NULL && pHead2 == NULL){
n->next = pHead1;
pHead1 = pHead1->next;
n=n->next;
}else if(pHead1 == NULL && pHead2 != NULL){
n->next = pHead2;
pHead2 = pHead2->next;
n=n->next;
}
if(i==0) {start = n;i++;}
}
return start;
}
结果1:
通过。看看别人更高效的办法。
还有递归版本:
ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
{
ListNode* node=NULL;
if(pHead1==NULL){return node=pHead2;}
if(pHead2==NULL){return node=pHead1;}
if(pHead1->val>pHead2->val){
node=pHead2;
node->next=Merge(pHead1,pHead2->next);
}else
{
node=pHead1;
node->next=Merge(pHead1->next,pHead2);
}
return node;
}
树的子结构
题目:输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)
思考1:参考了讨论,使用递归的思想,一个函数的时候不能处理全部情况。使用两个函数,递归判断,左右子树。
代码1:
bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2)
{
if(pRoot2 == NULL || pRoot1 == NULL){
return false;
}else{
return isSubtree(pRoot1, pRoot2) || HasSubtree(pRoot1->left, pRoot2) || HasSubtree(pRoot1->right, pRoot2) ;
}
}
bool isSubtree(TreeNode* pRoot1, TreeNode* pRoot2)
{
if(pRoot2 == NULL){ return true;}
if(pRoot1 == NULL){ return false;}
if(pRoot2->val == pRoot1->val){
return isSubtree(pRoot1->left, pRoot2->left) && isSubtree(pRoot1->right, pRoot2->right);
}else {return false;}
}
结论1:
通过。一开始想通过中序遍历什么的判断。想不出来就参考了下讨论。
二叉树的镜像
题目:操作给定的二叉树,将其变换为源二叉树的镜像。
思考1:使用BFS,不过从右边开始遍历,然后空的用NULL
代码1:
结果1:想不出来
思考2:从上到下递归交换左右节点
代码2:
void Mirror(TreeNode *pRoot) {
if(pRoot!=NULL && ( pRoot->right !=NULL ||pRoot->left !=NULL)){
TreeNode *node = pRoot->right;
pRoot->right = pRoot->left;
pRoot->left = node;
if( node ->right!=NULL ){
Mirror(node ->right);
}
if(node ->left!=NULL){
Mirror(node ->left);
}
}
return ;
}
结果2:
段错误:您的程序发生段错误,可能是数组越界,堆栈溢出(比如,递归调用层数太多)等情况引起
case通过率为0.00%
逻辑正确,不知道哪里错了,和别人的相似
顺时针打印矩阵
题目:输入一个矩阵,按照从外向里以顺时针的顺序依次打印出每一个数字,例如,如果输入如下4 X 4矩阵: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10。
思考1:手动画一下逻辑,向右---》向下---》向左----》向上。走到界限就转向,并且更新界限。
代码1:
vector printMatrix(vector > matrix) {
vector result;
if(matrix.empty()) return result;
int c = matrix[0].size();
int k = matrix.size();
int re = matrix[0].size()-1;
int de = matrix.size()-1;
int le = 0;
int ue = 0;
char flag = 'r'; //r---d----l----u
int num = 0;
int x = 0;
int y = 0;
while( num < c*k ){
switch(flag){
case 'r':
if(x <= re){
result.push_back(matrix[y][x]);
num++;
x++;
}else{
x = re ;
y = ue + 1;
flag = 'd';
ue++;
}
break;
case 'd':
if(y <= de){
result.push_back(matrix[y][x]);
num++;
y++;
}else{
x = re - 1;
y = de;
flag = 'l';
re--;
}
break;
case 'l':
if(x >= le){
result.push_back(matrix[y][x]);
num++;
x--;
}else{
x = le;
y = de - 1;
flag = 'u';
de -- ;
}
break;
case 'u':
if(y >= ue){
result.push_back(matrix[y][x]);
num++;
y--;
}else{
x = le + 1;
y = ue ;
flag = 'r';
le ++ ;
}
break;
}
}
return result;
}
结果1:通过了。
包含min函数的栈
题目:定义栈的数据结构,请在该类型中实现一个能够得到栈中所含最小元素的min函数(时间复杂度应为O(1))。
思考1:一个正常,一个计算min的两个栈。主要在POP和PUSH里面判断更新min栈的数。
代码1:
stack mystack;
stack mystack2;
void push(int value) {
mystack.push(value);
if(mystack2.empty()){
mystack2.push(value);
}else{
int mymin = mystack2.top();
if(mymin>value){
mystack2.push(value);
}
}
}
void pop() {
int p = mystack.top();
mystack.pop();
if(p == mystack2.top()) mystack2.pop();
}
int top() {
return mystack.top();
}
int min() {
return mystack2.top();
}
结果1:
通过。
栈的压入、弹出序列
题目1:输入两个整数序列,第一个序列表示栈的压入顺序,请判断第二个序列是否可能为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序,序列4,5,3,2,1是该压栈序列对应的一个弹出序列,但4,3,5,1,2就不可能是该压栈序列的弹出序列。(注意:这两个序列的长度是相等的)
思考1:
参考讨论,弄个辅助栈,来模拟出栈。
代码1:
bool IsPopOrder(vector pushV,vector popV) {
stack myvt3;
int n = 0;
for(int i = 0 ; i 结果1:
通过。
从上往下打印二叉树
题目:从上往下打印出二叉树的每个节点,同层节点从左至右打印。
思考1:BFS。
代码1:
vector PrintFromTopToBottom(TreeNode* root) {
vector result;
if (root == NULL) {
return result;
}
queue a;
TreeNode* b;
a.push(root);
while(!a.empty()){
b = a.front();
result.push_back(b->val);
a.pop();
if(b->left!=NULL) a.push(b->left);
if(b->right!=NULL) a.push(b->right);
}
return result;
}
结果1:
BFS使用队列,DFS使用栈。
二叉树的后序遍历
题目:输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。
思考1:
二叉查找树(Binary Search Tree),(又:二叉搜索树,二叉排序树)它或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。根据它的特性,最后一个值为根,中间可以根据第一个大于根的数值分成左子树,右子树。右子树如果大于根则是错误的,递归判断左右子树。
代码1:
bool judge(vector& a, int b, int c){
int root = a[c];
int num = 0 ;
bool flag = true;
if(b>=c) return true;
for(int i = b; i < c;i++){
if(a[i]>root && flag){
num = i;
flag = !flag;
}
if(a[i] sequence) {
if(sequence.empty()) return false;
bool flag = judge(sequence, 0 , sequence.size()-1);
return flag;
}
结果1:
通过。
二叉树中和为某一值的路径
题目:
输入一颗二叉树的跟节点和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中,数组长度大的数组靠前)
思考1:DFS,到达根后统计和,如果是符合的,则加入到输出列表中
代码1:
void DFS(TreeNode* root,int a,int result, vector valList, vector > &revalList) {
int b = root->val;
int sum = a + b;
valList.push_back(b);
if(root->left == NULL && root->right == NULL){
if(sum == result){
revalList.push_back(valList);
return ;
}
}else{
if(root->left != NULL) DFS(root->left, sum, result, valList, revalList);
if(root->right != NULL) DFS(root->right, sum, result, valList, revalList);
}
}
vector > FindPath(TreeNode* root,int expectNumber) {
vector valList;
vector > re;
if(root == NULL) return re;
valList.push_back(root->val);
if(root->left != NULL) DFS(root->left, root->val, expectNumber, valList, re);
if(root->right != NULL) DFS(root->right, root->val, expectNumber, valList, re);
if(root->right == NULL && root->left == NULL && root->val==expectNumber) re.push_back(valList);
return re;
}
结果1:
成功。注意考虑多种情况的判断。
复杂链表的复制
思考1:直接遍历的时候链接random和next
代码1:
RandomListNode* Clone(RandomListNode* pHead)
{
RandomListNode* newHead = new RandomListNode(pHead->label);
//newHead.label=(pHead->label);
// if(pHead->random!=NULL){
newHead->random = pHead->random;
//}
RandomListNode* op = pHead->next;
RandomListNode* np = newHead;
while(op!=NULL){
np->next = op;
np->next->random = op->random;
// cout <<100+op->label<label<next;
np = np->next;
}
return newHead;
}
结果1:
空.请检查一下你的代码,有没有循环输入处理多个case.点击查看如何处理多个case。好像是不能直接这样做,而是要复制出来新的一份。
思路2:
复制每个点生成链表,链接random。
代码2:
RandomListNode* Clone(RandomListNode* pHead)
{
if (pHead == NULL) return NULL;
RandomListNode* newHead = new RandomListNode(pHead->label);
RandomListNode* op = pHead;
RandomListNode* np = newHead;
while(op->next){
RandomListNode* tmp = new RandomListNode(op->next->label);
np->next = tmp;
op = op->next;
np = np->next;
}
op = pHead;
np = newHead;
while(op){
if(op->random){
RandomListNode* tmp = new RandomListNode(op->random->label);
np->random = tmp;
}
op = op->next;
np = np->next;
}
return newHead;
}
结果2:虽然通过了。但是random链接的不一样,是new了个新的。
思考3:
参考书上的
-
把复制的结点链接在原始链表的每一对应结点后面
2. 把复制的结点的random指针指向被复制结点的random指针的下一个结点
3. 拆分成两个链表,奇数位置为原链表,偶数位置为复制链表,注意复制链表的最后一个结点的next指针不能跟原链表指向同一个空结点None,next指针要重新赋值None(判定程序会认定你没有完成复制)
代码3:
RandomListNode* Clone(RandomListNode* pHead)
{
if (pHead == NULL) return NULL;
RandomListNode* op = pHead;
while(op!=NULL){
RandomListNode* tmp = new RandomListNode(op->label);
tmp->next = op ->next;
op ->next = tmp;
op = op->next->next;
}
op = pHead;
while(op!=NULL){
if(op->random){
op->next->random = op->random->next;
}
op = op->next->next;
}
op = pHead;
RandomListNode* tmp;
RandomListNode* newHead = op->next;
while(op->next){
tmp = op->next;
op->next = op->next->next;
op = tmp;
}
return newHead;
}
结果3:
通过,但是分拆的时候,为什么不能是 while(op!=NULL)而是while(op->next)??
二叉搜索树与双向链表
题目:输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的双向链表。要求不能创建任何新的结点,只能调整树中结点指针的指向。
想法1:
使用中序遍历的方法,中序遍历能按顺序操作节点,引入一个pre指针,按顺序修改前后相邻的节点的左右指向。
代码1:
TreeNode* pre = nullptr;
void zhong(TreeNode* p)
{
if(!p) {return;}
zhong(p->left);
if(pre == nullptr){
pre = p;
}else{
pre->right = p;
p->left = pre;
pre = p;
}
zhong(p->right);
}
TreeNode* Convert(TreeNode* pRootOfTree)
{
if(pRootOfTree == nullptr) return nullptr; //注意这些判断,不加入会错误
zhong(pRootOfTree);
while(pRootOfTree->left){
pRootOfTree = pRootOfTree->left;
}
return pRootOfTree;
}
结果1:正确,参考了讨论。
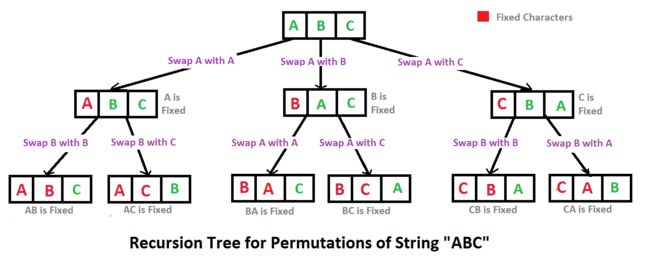
字符串的排列
题目:输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。
想法1:参考讨论,不会,以后重写。
代码1:
void todo(string s,int i,int j,vector &result){
if(j-i==1) {
result.push_back(s);
return;}
set r;
for(int m =i;m::iterator iter;
swap(s[i],s[m]);
if((iter = r.find(s)) == r.end())
{
r.insert(s);
todo(s,i+1,s.size(),result);
}
}
}
vector Permutation(string str) {
vector result;
if(str.size()==0) return result;
todo(str,0,str.size(),result);
sort(result.begin(),result.end());
return result;
}
结果1:
通过
数组中出现次数超过一半的数字
题目:数组中有一个数字出现的次数超过数组长度的一半,请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次,超过数组长度的一半,因此输出2。如果不存在则输出0。
想法1:
先把数组排序,然后遍历,遍历的时候统计相同的数目,如果有变化,说明统计数目得清空。如果有超过一半数目就可以直接输出,不用继续遍历。
代码1:
int MoreThanHalfNum_Solution(vector numbers) {
if(numbers.size()==1) return numbers.at(0);
sort(numbers.begin(),numbers.end());
int pre = 0;
int num = 0;
for(int i = 0 ; inumbers.size()/2){
return numbers.at(i);
}
}else{
num=1;
}
pre = numbers.at(i);
}
return 0;
}
结果1:
成功,注意一个长度的情况。
最小的K个数
题目:输入n个整数,找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字,则最小的4个数字是1,2,3,4,。
想法1:排序,输出前K个数目
代码1:
vector GetLeastNumbers_Solution(vector input, int k) {
vector result;
if(k > input.size()||input.empty())
{
return result;
}
sort(input.begin(),input.end());
for(int i = 0 ; i 结果1:
通过,注意k大于长度,要输出空。
连续子数组的最大和
题目::
HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢?例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组,返回它的最大连续子序列的和,你会不会被他忽悠住?(子向量的长度至少是1)
想法1:滑动窗口模式,1个长度到N个长度,记录最大值
代码1:
int FindGreatestSumOfSubArray(vector array) {
int m = INT_MIN;
for(int i = 1;i 结果1:
通过,但是没有用到动态规划想法,参考讨论。
想法2:
使用动态规划
F(i):以array[i]为末尾元素的子数组的和的最大值,子数组的元素的相对位置不变
F(i)=max(F(i-1)+array[i] , array[i])
res:所有子数组的和的最大值
res=max(res,F(i))
如数组[6, -3, -2, 7, -15, 1, 2, 2]
初始状态:
F(0)=6
res=6
i=1:
F(1)=max(F(0)-3,-3)=max(6-3,3)=3
res=max(F(1),res)=max(3,6)=6
i=2:
F(2)=max(F(1)-2,-2)=max(3-2,-2)=1
res=max(F(2),res)=max(1,6)=6
i=3:
F(3)=max(F(2)+7,7)=max(1+7,7)=8
res=max(F(2),res)=max(8,6)=8
i=4:
F(4)=max(F(3)-15,-15)=max(8-15,-15)=-7
res=max(F(4),res)=max(-7,8)=8
以此类推
最终res的值为8
代码2:
int FindGreatestSumOfSubArray(vector array) {
int m = array.at(0);
int nowsum = array.at(0);
for(int i = 1;i 结果2:
参考讨论。
整数中1出现的次数(从1到n整数中1出现的次数)
题目:求出113的整数中1出现的次数,并算出1001300的整数中1出现的次数?为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数(从1 到 n 中1出现的次数)。
想法1:
把数字转成字符串,然后遍历字符串
代码1:
int NumberOf1Between1AndN_Solution(int n)
{
int number = 0;
for(int i = 1 ;i <= n;i++){
string s=to_string(i);
for(int j =0 ;j < s.length();j++){
if( s[j] == '1'){
number = number + 1;
}
}
}
return number;
}
结果1:
通过,但是太暴力了?看看讨论的方法
想法2:
代码2:
结果2:
把数组排成最小的数
题目:输入一个正整数数组,把数组里所有数字拼接起来排成一个数,打印能拼接出的所有数字中最小的一个。例如输入数组{3,32,321},则打印出这三个数字能排成的最小数字为321323。
想法1:
两两组合,最大的放后面,冒泡排序
代码1:
string PrintMinNumber(vector numbers) {
vector str_numbers;
string result = "";
for(int i = 0;istr_numbers[j+1]+str_numbers[j]){
string temp = str_numbers[j+1];
str_numbers[j+1] = str_numbers[j];
str_numbers[j] = temp;
}
}
}
for(int i = 0;i 结果1:
通过
想法2:讨论里,使用sort,重写比较器
代码2:
static bool compare( const string &st1,const string &st2){
string s1 = st1+st2;
string s2 = st2+st1;
return s1丑数
题目:把只包含质因子2、3和5的数称作丑数(Ugly Number)。例如6、8都是丑数,但14不是,因为它包含质因子7。 习惯上我们把1当做是第一个丑数。求按从小到大的顺序的第N个丑数。
想法1:
找不到规律,参考讨论。
说下思路,如果p是丑数,那么p=2^x * 3^y * 5^z
那么只要赋予x,y,z不同的值就能得到不同的丑数。
如果要顺序找出丑数,要知道下面几个特(fei)点(hua)。
对于任何丑数p:
(一)那么2p,3p,5p都是丑数,并且2p<3p<5p
(二)如果p
现在说说算法思想:
由于1是最小的丑数,那么从1开始,把21,31,51,进行比较,得出最小的就是1
的下一个丑数,也就是21,
这个时候,多了一个丑数‘2’,也就又多了3个可以比较的丑数,22,32,52,
这个时候就把之前‘1’生成的丑数和‘2’生成的丑数加进来也就是
(31,51,22,32,52)进行比较,找出最小的。。。。如此循环下去就会发现,
每次选进来一个丑数,该丑数又会生成3个新的丑数进行比较。
上面的暴力方法也应该能解决,但是如果在面试官用这种方法,估计面试官只会摇头吧
。下面说一个O(n)的算法。
在上面的特(fei)点(hua)中,既然有p
“我”在前面比你小的数都没被选上,你后面生成新的丑数一定比“我”大吧,那么你乘2
生成的丑数一定比我乘2的大吧,那么在我选上之后你才有机会选上。
其实每次我们只用比较3个数:用于乘2的最小的数、用于乘3的最小的数,用于乘5的最小的
数。也就是比较(2x , 3y, 5*z) ,x>=y>=z的,
重点说说下面代码中p的作用:int p[] = new int[] { 0, 0, 0 }; p[0]表示最小用于
乘2比较数在数组a中的【位置】。
代码1:
int GetUglyNumber_Solution(int index) {
if(index == 0) return 0;
if(index == 1) return 1;
int p[3]={0,0,0};
vector result;
result.push_back(1);
for(int i=1;i 结果1:
通过,注意特殊点0和1的判断。
第一个只出现一次的字符
题目:
在一个字符串(0<=字符串长度<=10000,全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1(需要区分大小写).
想法1:
两个数组,一个存字符,一个存字符的符合资格,如果出现多次,失去资格,最后返回资格符合的字符的位置。
代码1:
int FirstNotRepeatingChar(string str) {
vector word;
vector word2;
for(int i = 0;i:: iterator iVector;
iVector = std::find(word.begin(), word.end(), str[i]);
if(iVector!= word.end())
{
int nPosition = distance(word.begin(),iVector);
word2[nPosition] = '#';
}
else
{
word.push_back(str[i]);
word2.push_back(str[i]);
}
}
for(int i = 0;i 结果1:
通过,看看评论有什么好办法
方法2:
//直接使用map
class Solution {
public:
int FirstNotRepeatingChar(string str) {
map mp;
for(int i = 0; i < str.size(); ++i)
mp[str[i]]++;
for(int i = 0; i < str.size(); ++i){
if(mp[str[i]]==1)
return i;
}
return -1;
}
};
数组中的逆序对
题目:在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007
想法1:暴力每个数字和后续的对比大小,复杂度o(n^2)
代码1:
int InversePairs(vector data) {
int c = 0;
for(int i = 0 ; idata[j]){
c++;
}
}
}
return c%1000000007;
}
结果1:
您的程序未能在规定时间内运行结束,请检查是否循环有错或算法复杂度过大。
想法2:
归并排序的想法,加入判断逆序
代码2:
int cou=0;
void mymerge(vector& data,int first, int mid , int last,vector& temp){
int f = first;
int l = mid+1;
int k = 0;
while(f<=mid&&l<=last){
if(data[f]>data[l]){
temp[k++]=data[l++];
cou=(cou+(mid-f+1))%1000000007;
}else
temp[k++]=data[f++];
}
while(f<=mid){
temp[k++]=data[f++];
}
while(l<=last){
temp[k++]=data[l++];
}
for(int i =0;i& data, int first, int last,vector& temp){
if(first data) {
if(data.size()==0) return 0;
vector temp = data;
dive(data, 0, data.size()-1,temp);
return cou;
}
结果2:
学习归并的模式,递归进入最细粒度的分解后进行归并。
两个链表的第一个公共结点
题目:输入两个链表,找出它们的第一个公共结点。
想法1:公共节点后面都相同,先求长度,然后长的走长度差,然后一起走,如果两个点相等,那么到了公共点。
代码1:
ListNode* FindFirstCommonNode( ListNode* pHead1, ListNode* pHead2) {
int l1=1;
int l2=1;
ListNode *p1=pHead1;
ListNode *p2=pHead2;
while(p1!=NULL){
p1=p1->next;
l1++;
}
while(p2!=NULL){
p2=p2->next;
l2++;
}
p1=pHead1;
p2=pHead2;
if(l1>=l2){
int c =l1-l2;
while(c>0){
p1=p1->next;
c--;
}
}else{
int c =l2-l1;
while(c>0){
p2=p2->next;
c--;
}
}
while(p2!=NULL){
if(p1==p2){
return p1;
}
p1=p1->next;
p2=p2->next;
}
return NULL;
}
结果1:
通过。
想发2:
讨论中用hashmap,先放链表1,遍历链表2的时候查询map中有无同一个点。
数字在排序数组中出现的次数
题目:统计一个数字在排序数组中出现的次数。
想法1:遍历,统计
代码1:
int c = 0;
for(int i =0;i结果1:
通过。
想法2:想法一太简单了哈哈哈,这种题目应该想到二分法,参考讨论。找出最左和最右的K位置,二分法有递归和循环两种写法。
二叉树的深度
题目:
输入一棵二叉树,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。
想法1:
使用BFS遍历,每层加一个深度。但是得学会递归版和非递归版
代码1:
//非递归版
int TreeDepth2(TreeNode* pRoot)
{
int depth = 0;
if(pRoot){
queue q;
q.push(pRoot);
while(!q.empty()){
for(int i =0,n=q.size();ileft) q.push(node->left);
if(node->right) q.push(node->right);
}
depth++;
}
}
return depth;
}
//递归版
//左子树,右子树只有一个,那么那个树的深度+1,都有的话是两者最大深度加1
int TreeDepth2(TreeNode* pRoot)
{
int depth = 0;
if(!pRoot) return 0;
if(!pRoot->left&&!pRoot->right) return 1;
if(pRoot->left&&!pRoot->right) depth = TreeDepth2(pRoot->left)+1;
if(!pRoot->left&&pRoot->right) depth = TreeDepth2(pRoot->right)+1;
if(pRoot->left&&pRoot->right) depth = max(TreeDepth2(pRoot->left)+1,TreeDepth2(pRoot->right)+1);
return depth;
}
结果1:
BFS用队列,DFS用栈
平衡二叉树
题目:输入一棵二叉树,判断该二叉树是否是平衡二叉树。
想法1:判断每个节点的左右子树是不是平衡二叉树。
代码1:
int TreeDepth2(TreeNode* pRoot)
{
int depth = 0;
if(!pRoot) return 0;
if(!pRoot->left&&!pRoot->right) return 1;
if(pRoot->left&&!pRoot->right) depth = TreeDepth2(pRoot->left)+1;
if(!pRoot->left&&pRoot->right) depth = TreeDepth2(pRoot->right)+1;
if(pRoot->left&&pRoot->right) depth = max(TreeDepth2(pRoot->left)+1,TreeDepth2(pRoot->right)+1);
return depth;
}
//DFS
bool IsBalanced_Solution(TreeNode* pRoot) {
bool flag =true;
if(pRoot){
stack q;
q.push(pRoot);
while(!q.empty()){
TreeNode* temp = q.top();
q.pop();
if(temp->left&&!temp->right) {if(TreeDepth2(temp->left)>1)
{
flag =false ;
return flag;
}
}
if(!temp->left&&temp->right) {if(TreeDepth2(temp->right)>1)
{
flag =false ;
return flag;
}
}
if(temp->left&&temp->right) {if(abs(TreeDepth2(temp->right)-TreeDepth2(temp->left))>1)
{
flag =false ;
return flag;
}
}
if(temp->left) q.push(temp->left);
if(temp->right) q.push(temp->right);
}
}
return flag;
}
//BFS
bool IsBalanced_Solution2(TreeNode* pRoot)
{
bool flag = true;
if(pRoot){
queue q;
q.push(pRoot);
while(!q.empty()){
for(int i =0,n=q.size();iright)-TreeDepth2(node->left))>1){
flag =false;
return flag;
}
q.pop();
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
}
}
return flag;
}
结果1:
看看讨论有无技巧。
想法2:
从上到下有些节点重复计算,可以从小而上,剪枝
代码2:
//就是我的DFS?
public boolean IsBalanced_Solution(TreeNode root) {
return getDepth(root) != -1;
}
private int getDepth(TreeNode root) {
if (root == null) return 0;
int left = getDepth(root.left);
if (left == -1) return -1;
int right = getDepth(root.right);
if (right == -1) return -1;
return Math.abs(left - right) > 1 ? -1 : 1 + Math.max(left, right);
}
数组中只出现一次的数字
题目:一个整型数组里除了两个数字之外,其他的数字都出现了两次。请写程序找出这两个只出现一次的数字。
想法1:参考讨论。题目中的两次和一次是关键字,可以通过异或运算,消除两次的数字。最后是两个一次的数字的异或值,并且找出最低位为1的数位,然后把原来的数组按这个数位是不是为1分成两组数字。两组数字中再分别进行异或,因为每组都是一个一次的和多个两次的数字集合。
代码1:
void FindNumsAppearOnce(vector data,int* num1,int *num2) {
if(data.size()==0) return;
int xo=data[0];
for(int i =1;i>1;
index++;
}
*num1=0;
*num2=0;
for(int i =0;i>index&1)==1)
*num1=*num1^data[i];
else
*num2=*num2^data[i];
}
}
结果1:
&运算通常用于二进制取位操作,例如一个数 &1的结果就是取二进制的最末位;
a<
不会有影响的,任何数和0异或得到本身:如果数组中0出现了两次,则数组中两数异或为0;如果0出现了一次,就直接是0。所以num1和num2初始化是就是0
和为S的连续正数序列
题目:小明很喜欢数学,有一天他在做数学作业时,要求计算出9~16的和,他马上就写出了正确答案是100。但是他并不满足于此,他在想究竟有多少种连续的正数序列的和为100(至少包括两个数)。没多久,他就得到另一组连续正数和为100的序列:18,19,20,21,22。现在把问题交给你,你能不能也很快的找出所有和为S的连续正数序列? Good Luck!
想法1:
从1遍历到一半,连续相加,如果正好说明找到了,大于说明不行。
代码1:
vector > FindContinuousSequence(int sum) {
vector > result;
vector r;
for(int i =1;i<(sum/2+1);i++){
int s = i;
r.push_back(i);
for(int j = i+1;j<(sum/2+2);j++){
r.push_back(j);
s+=j;
if(s==sum){
result.push_back(r);
r.clear();
}
if(s>sum){
r.clear();
continue;
}
}
}
return result;
}
结果1:
比较暴力?注意 for(int j = i+1;j<(sum/2+2);j++) ,不加2的话,两位数的不能判断。看看讨论的技巧。
想法2:
说的很好,叫做双指针技术,就是相当于有一个窗口,窗口的左右两边就是两个指针,我们根据窗口内值之和来确定窗口的位置和宽度。
和为S的两个数字
题目:输入一个递增排序的数组和一个数字S,在数组中查找两个数,使得他们的和正好是S,如果有多对数字的和等于S,输出两个数的乘积最小的。
想法1:
两个指针1,2,1从第一个开始,2从最后个开始。如果2找到了,那么下次可以直接从2开始遍历。
代码1:
vector FindNumbersWithSum(vector array,int sum) {
vector result;
int o = -1;
int t = -1;
int high = array.size()-1;
int m = 0;
for(int i = 0 ;ii;j--){
if(array[i]+array[j]==sum){
high = j;
if(o + t < 0){
o = i;
t = j;
m = array[i]*array[j];
continue;
}
if(array[i]*array[j]0){
result.push_back(array[o]);
result.push_back(array[t]);
}
return result;
}
结果1:
通过。看看讨论。
想法2:
第一组就是乘机最小的,也是左右两个指针,方法比我的好,左边也优化了。
代码2:
vector FindNumbersWithSum(vector a,int sum) {
vector result;
int low = 0;
int high = a.size()-1;
while(lowsum) high--;
if((a[low]+a[high]) 左旋转字符串
题目:汇编语言中有一种移位指令叫做循环左移(ROL),现在有个简单的任务,就是用字符串模拟这个指令的运算结果。对于一个给定的字符序列S,请你把其循环左移K位后的序列输出。例如,字符序列S=”abcXYZdef”,要求输出循环左移3位后的结果,即“XYZdefabc”。是不是很简单?OK,搞定它!
想法1:
找出头几个和后面的字符串,组合
代码1:
string LeftRotateString(string str, int n) {
int le = str.size();
string result ;
if(le == 0) return result;
string a = str.substr(0,n%le);
string b = str.substr(n%le);
result = b + a;
return result;
}
结果:
注意判断n超过字符串长度的情况。看看讨论的想法。
想法2:
好像直接用API不太好???自己实现算法。。。。。
翻转单词顺序列
题目:牛客最近来了一个新员工Fish,每天早晨总是会拿着一本英文杂志,写些句子在本子上。同事Cat对Fish写的内容颇感兴趣,有一天他向Fish借来翻看,但却读不懂它的意思。例如,“student. a am I”。后来才意识到,这家伙原来把句子单词的顺序翻转了,正确的句子应该是“I am a student.”。Cat对一一的翻转这些单词顺序可不在行,你能帮助他么?
想法1:
按空格切分,保存每个字符的开始,结束位置,从后到前重新生成字符串
代码1:
string ReverseSentence(string str) {
string result = "";
if(str.size()==0) return result;
vector b={0};
for(int i = 0 ;i=0;j--){
string s(str,b[2*j],b[2*j+1]-b[2*j]+1);
result+=s;
if(j!=0){
result+=' ';
}
}
return result;
}
结果1:
通过,看看别人想法。
想法2:
一个个遍历,一组字符加入到后面。
string res = "", tmp = "";
for(unsigned int i = 0; i < str.size(); ++i){
if(str[i] == ' ') res = " " + tmp + res, tmp = "";
else tmp += str[i];
}
if(tmp.size()) res = tmp + res;
return res;
扑克牌顺子
题目:LL今天心情特别好,因为他去买了一副扑克牌,发现里面居然有2个大王,2个小王(一副牌原本是54张_)...他随机从中抽出了5张牌,想测测自己的手气,看看能不能抽到顺子,如果抽到的话,他决定去买体育彩票,嘿嘿!!“红心A,黑桃3,小王,大王,方片5”,“Oh My God!”不是顺子.....LL不高兴了,他想了想,决定大\小 王可以看成任何数字,并且A看作1,J为11,Q为12,K为13。上面的5张牌就可以变成“1,2,3,4,5”(大小王分别看作2和4),“So Lucky!”。LL决定去买体育彩票啦。 现在,要求你使用这幅牌模拟上面的过程,然后告诉我们LL的运气如何, 如果牌能组成顺子就输出true,否则就输出false。为了方便起见,你可以认为大小王是0。
想法1:
除了百变的0,如果有相同数字就不行,如果最小和最大的数字相差大于4,那也不行,百变也救不了。
代码1:
bool IsContinuous( vector numbers ) {
int le = numbers.size();
if(le==0) return false;
sort(numbers.begin(),numbers.end());
for(int i =0;i< le-1;i++){
if(numbers[i]!=0){
if(numbers[i]==numbers[i+1])
return false;
}
}
int ma = numbers[numbers.size()-1];
int mi = 0;
for(int i =0;i< le;i++){
if(numbers[i]!=0){
{mi = numbers[i];
break;
}
}
}
if(ma-mi<=4) return true;
return false;
}
结果1:
通过,看看别人的想法。好像都要加入size==0判断?不然会溢出情况。
想法2:
孩子们的游戏(圆圈中最后剩下的数)
题目:每年六一儿童节,牛客都会准备一些小礼物去看望孤儿院的小朋友,今年亦是如此。HF作为牛客的资深元老,自然也准备了一些小游戏。其中,有个游戏是这样的:首先,让小朋友们围成一个大圈。然后,他随机指定一个数m,让编号为0的小朋友开始报数。每次喊到m-1的那个小朋友要出列唱首歌,然后可以在礼品箱中任意的挑选礼物,并且不再回到圈中,从他的下一个小朋友开始,继续0...m-1报数....这样下去....直到剩下最后一个小朋友,可以不用表演,并且拿到牛客名贵的“名侦探柯南”典藏版(名额有限哦!!_)。请你试着想下,哪个小朋友会得到这份礼品呢?(注:小朋友的编号是从0到n-1)
想法1:使用链表模拟游戏过程,最后一个就是。
代码1:
int LastRemaining_Solution(int n, int m)
{
if(n<=0||m<=0) return -1;
if(m==1||n==1) return n-1;
ListNode a(0);
ListNode *temp;
ListNode *p =&a;
for(int i = 1;inext=temp;
p = p->next;
}
p->next=&a;
ListNode *temp2 = &a;
int cou=0;
while(temp2->next!=NULL){
if(temp2->val==temp2->next->val){break;}
if(cou==m-2){
temp2->next = temp2->next->next;
cou = 0;
temp2 = temp2->next;
continue;
}
temp2 = temp2->next;
cou++;
}
return temp2->val;
}
//模拟2
public class Solution {
public int LastRemaining_Solution(int n, int m) {
LinkedList list = new LinkedList();
for (int i = 0; i < n; i ++) {
list.add(i);
}
int bt = 0;
while (list.size() > 1) {
bt = (bt + m - 1) % list.size();
list.remove(bt);
}
return list.size() == 1 ? list.get(0) : -1;
}
}
结果1:
(0,0)的时候返回-1。
想法2:找规律,使用公式。
代码2:
结果2:
求1+2+3+...+n
题目:求1+2+3+...+n,要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句(A?B:C)。
想法1:使用递归啥的,不知道如何终止程序。
代码1:
结果1:
想法2:
使用&&或者||的短路思想来终止递归
代码2:
int sum = 0;
int Sum(int n) {
sum+=n;
return n&&Sum(--n);
}
int Sum_Solution(int n) {
Sum(n);
return sum;
}
//他们的
int Sum_Solution(int n) {
int ans = n;
ans && (ans += Sum_Solution(n - 1));
return ans;
}
不用加减乘除做加法
题目:写一个函数,求两个整数之和,要求在函数体内不得使用+、-、*、/四则运算符号。
想法1:使用++,--
代码1:
int Add(int num1, int num2)
{
if(num2>=0){
for(int i = 0;inum2;i--){
num1--;
}
}
return num1;
}
结果1:
通过,好像不行,看看讨论。
想法2:
使用位运算,不会
代码2:
把字符串转换成整数
题目:将一个字符串转换成一个整数(实现Integer.valueOf(string)的功能,但是string不符合数字要求时返回0),要求不能使用字符串转换整数的库函数。 数值为0或者字符串不是一个合法的数值则返回0。
想法1:
判断第一个正负,遍历数字提取出来,然后按位数生成。
代码1:
int StrToInt(string str) {
int le =str.size();
if(le==0) return 0;
char f = str[0];
int r = 0;
vector result;
for(int i =0;i=48&&str[i]<=57){
result.push_back(str[i]-48);
}else return 0;
}
int le2=result.size()-1;
for(int i =0;i < result.size();i++){
r=r+pow(10,le2--)*result[i];
}
if(f == '+'||f>=48&&f<=57){
return 0+r;
}
if(f == '-'){
return 0-r;
}
return 0;
}
结果1:
通过,查看讨论。
想法2:
int StrToInt(string str) {
int n = str.size(), s = 1;
long long res = 0;
if(!n) return 0;
if(str[0] == '-') s = -1;
for(int i = (str[0] == '-' || str[0] == '+') ? 1 : 0; i < n; ++i){
if(!('0' <= str[i] && str[i] <= '9')) return 0;
res = (res << 1) + (res << 3) + (str[i] & 0xf);//res=res*10+str[i]-'0';
//和res=res*10+str[i]-'0'是一样的。左移是乘以2的次方。(res << 1) + (res << 3) = res * 2 + res * 8 = res * 10 。 字符'0'到'9'的ascii值的低4个二进制位刚好就是0到9所以str[i]&0xf等于str[i]-'0'。
}
return res * s;
}
数组中重复的数字
题目:在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的,但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如,如果输入长度为7的数组{2,3,1,0,2,5,3},那么对应的输出是第一个重复的数字2。
想法1:排序,遍历,相同输出
代码1:
bool duplicate(int numbers[], int length, int* duplication) {
if(length == 0) return false;
sort(&numbers[0],&numbers[length-1]);
for(int i =0;i结果1:
通过,看看讨论。
想法2:
使用一个数组来作为标志数组来统计数字的个数,大于1就说明重复了。
代码2:
bool duplicate(int numbers[], int length, int* duplication) {
if(length == 0) return false;
int n[length];
for(int i =0;i1){
*duplication = numbers[i];
return true;
}
}
return false;
}
结果:
通过。
构建乘积数组
题目:给定一个数组A[0,1,...,n-1],请构建一个数组B[0,1,...,n-1],其中B中的元素B[i]=A[0]A[1]...A[i-1]A[i+1]...A[n-1]。不能使用除法。
想法1:算左边部分和右边部分。
代码1:
vector result;
vector result2;
vector result3;
int le =A.size();
for(int i =0;i=0;i--){
if(i==le-1){
result2.push_back(1);
continue;
}
result2.push_back(result2[l++]*A[i+1]);
}
for(int i =0;i 结果1:
看看讨论的优化版本。
代码2:
public int[] multiply(int[] A) {
int length = A.length;
int[] B = new int[length];
if(length != 0 ){
B[0] = 1;
//计算下三角连乘
for(int i = 1; i < length; i++){
B[i] = B[i-1] * A[i-1];
}
int temp = 1;
//计算上三角
for(int j = length-2; j >= 0; j--){
temp *= A[j+1];
B[j] *= temp;
}
}
return B;
}
结果2:
使用了temp记录了上三角的结果,比我使用数组记录的好。
正则表达式匹配
题目:请实现一个函数用来匹配包括'.'和''的正则表达式。模式中的字符'.'表示任意一个字符,而''表示它前面的字符可以出现任意次(包含0次)。 在本题中,匹配是指字符串的所有字符匹配整个模式。例如,字符串"aaa"与模式"a.a"和"abaca"匹配,但是与"aa.a"和"ab*a"均不匹配
想法1:
参考讨论。
解这题需要把题意仔细研究清楚,反正我试了好多次才明白的。
首先,考虑特殊情况:
1>两个字符串都为空,返回true
2>当第一个字符串不空,而第二个字符串空了,返回false(因为这样,就无法
匹配成功了,而如果第一个字符串空了,第二个字符串非空,还是可能匹配成
功的,比如第二个字符串是“a*a*a*a*”,由于‘*’之前的元素可以出现0次,
所以有可能匹配成功)
之后就开始匹配第一个字符,这里有两种可能:匹配成功或匹配失败。但考虑到pattern
下一个字符可能是‘*’, 这里我们分两种情况讨论:pattern下一个字符为‘*’或
不为‘*’:
1>pattern下一个字符不为‘*’:这种情况比较简单,直接匹配当前字符。如果
匹配成功,继续匹配下一个;如果匹配失败,直接返回false。注意这里的
“匹配成功”,除了两个字符相同的情况外,还有一种情况,就是pattern的
当前字符为‘.’,同时str的当前字符不为‘\0’。
2>pattern下一个字符为‘*’时,稍微复杂一些,因为‘*’可以代表0个或多个。
这里把这些情况都考虑到:
a>当‘*’匹配0个字符时,str当前字符不变,pattern当前字符后移两位,
跳过这个‘*’符号;
b>当‘*’匹配1个或多个时,str当前字符移向下一个,pattern当前字符
不变。(这里匹配1个或多个可以看成一种情况,因为:当匹配一个时,
由于str移到了下一个字符,而pattern字符不变,就回到了上边的情况a;
当匹配多于一个字符时,相当于从str的下一个字符继续开始匹配)
之后再写代码就很简单了。
代码1:
bool match(char* str, char* pattern)
{
if(*str=='\0'&&*pattern=='\0') return true;
if(*str!='\0'&&*pattern=='\0') return false;
while(*str!='\0'||(*pattern!='\0')){
if(*pattern=='\0') break;
if(*(pattern+1)=='*'){
if(*str==*pattern){
str++;
continue;
}
if(*str!=*pattern){
if(*(pattern)=='.'&&*str!='\0'){
if(*str!='\0') str++;
continue;
}
pattern++;
pattern++;
continue;
}
}else if(*(pattern)=='.'&&*str!='\0'||*str==*pattern){
pattern++;
str++;
continue;
}
return false;
}
if(*str!='\0') return false;
return true;
}
结果1:
"aaa","aa",我的判断错误,因为a可以走也可以不走,我这个方式不能两者同时判断,用递归。
代码2:
if(*str=='\0'&&*pattern=='\0') return true;
if(*str!='\0'&&*pattern=='\0') return false;
if(*(pattern+1)=='*'){
if(*(pattern)=='.'&&*str!='\0'||*str==*pattern)
return match(str+1,pattern)|| match(str,pattern+2);
else
return match(str,pattern+2);
}else {
if(*(pattern)=='.'&&*str!='\0'||*str==*pattern)
{
return match(str+1,pattern+1);
}
return false;
}
表示数值的字符串
题目:请实现一个函数用来判断字符串是否表示数值(包括整数和小数)。例如,字符串"+100","5e2","-123","3.1416"和"-1E-16"都表示数值。 但是"12e","1a3.14","1.2.3","+-5"和"12e+4.3"都不是。
想法1:
“.”,“e,E”,“+-”对这些字符设置标志位
代码1:
bool isNumeric(char* string)
{
if(*string =='\0') return false;
bool f1 = false; //fuhao
bool f2 = false; //xiaoshudian
bool f3 = false; //e
bool f4 = false; //shou
while(*string !='\0'){
if(*string!='+' &&*string!='-'&&*string!='e'&&*string!='E'&&*string!='.'&&(*string <'0'||*string >'9' )) return false;
if(*string=='+' || *string=='-'){
if(!f1&&(*(string-1)=='e'||*(string-1)=='E'||!f4)) {f1 = !f1;}
else {return false;}
}
if(*string=='.'){
if(!f2&&*(string+1)!='\0') f2 = !f2;
else return false;
}
if(*string=='e'||*string=='E'){
if(!f3&&*(string+1)!='\0') {
f3 = !f3;
f1 = false;
f2 = true;
}
else return false;
}
f4=true;
string++;
}
return true;
结果1:
通过,看看别人的想法。
想法2:
字符流中第一个不重复的字符
题目:请实现一个函数用来找出字符流中第一个只出现一次的字符。例如,当从字符流中只读出前两个字符"go"时,第一个只出现一次的字符是"g"。当从该字符流中读出前六个字符“google"时,第一个只出现一次的字符是"l"。
想法1:散列表统计个数。队列按顺序保存字符种类。
代码1:
char hash2[256]={0};
queue result;
void Insert(char ch)
{
hash2[ch-'\0']++;
if(hash2[ch-'\0']==1) result.push(ch);
}
//return the first appearence once char in current stringstream
char FirstAppearingOnce()
{
while(!result.empty()){
if(hash2[result.front()-'\0']==1)
return result.front();
else
result.pop();
}
return '#';
}
结果1:
通过。
链表中环的入口结点
题目:给一个链表,若其中包含环,请找出该链表的环的入口结点,否则,输出null。
想法1:一直遍历,如果回到同一个点就是入口,如果到NULL,就是没有。
代码1:
bool operator == (const ListNode& left, const ListNode& rigt)
{
return left.val == rigt.val && left.next == rigt.next;
}
ListNode* EntryNodeOfLoop(ListNode* pHead)
{
ListNode* result;
vector b;
while(pHead!=NULL){
vector::iterator r = find(b.begin(),b.end(),*pHead);
if(r == b.end())
{
b.push_back(*pHead);
}
else
{
result = pHead;
return result;
}
pHead=pHead->next;
}
return NULL;
}
结果1:
本地通过,在线不通过。看看讨论。
想法2:
使用set的属性
ListNode* EntryNodeOfLoop(ListNode* pHead)
{
ListNode* result;
set r;
while(pHead!=NULL){
if(!r.insert(pHead).second){
return pHead;
}
pHead=pHead->next;
}
return NULL;
}
想法3:
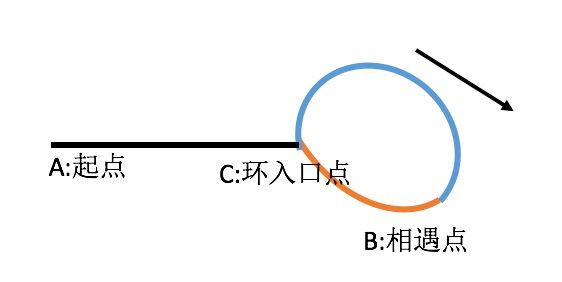
两个指针,快指针走慢指针的两倍速度,第一次相遇在环内,两者相差的长度是环的长度,然后一个指针原地走,一个指针从头重新走,再次相遇是在环入口。
假设x为环前面的路程(黑色路程),a为环入口到相遇点的路程(蓝色路程,假设顺时针走), c为环的长度(蓝色+橙色路程)
当快慢指针相遇的时候:
此时慢指针走的路程为Sslow = x + m * c + a
快指针走的路程为Sfast = x + n * c + a
2 Sslow = Sfast
2 * ( x + m*c + a ) = (x + n c + a)
从而可以推导出:
x = (n - 2 * m )c - a
= (n - 2 m -1 )c + c - a
即环前面的路程 = 数个环的长度(为可能为0) + c - a
什么是c - a?这是相遇点后,环后面部分的路程。(橙色路程)
所以,我们可以让一个指针从起点A开始走,让一个指针从相遇点B开始继续往后走,
2个指针速度一样,那么,当从原点的指针走到环入口点的时候(此时刚好走了x)
从相遇点开始走的那个指针也一定刚好到达环入口点。
所以2者会相遇,且恰好相遇在环的入口点。
最后,判断是否有环,且找环的算法复杂度为:
时间复杂度:O(n)
空间复杂度:O(1)
ListNode EntryNodeOfLoop(ListNode pHead){
if(pHead == null || pHead.next == null)
return null;
ListNode p1 = pHead;
ListNode p2 = pHead;
while(p2 != null && p2.next != null ){
p1 = p1.next;
p2 = p2.next.next;
if(p1 == p2){
p2 = pHead;
while(p1 != p2){
p1 = p1.next;
p2 = p2.next;
}
if(p1 == p2)
return p1;
}
}
return null;
}
删除链表中重复的结点
题目:在一个排序的链表中,存在重复的结点,请删除该链表中重复的结点,重复的结点不保留,返回链表头指针。 例如,链表1->2->3->3->4->4->5 处理后为 1->2->5。
想法1:设置一个计数数组,长度和链表长度一样。遍历的时候,如果当前和后一个相同,那么计数数组都+1。
代码1:
ListNode* deleteDuplication(ListNode* pHead)
{
ListNode* r = pHead;
if(r==NULL) return pHead;
ListNode* n = pHead->next;
if(n==NULL) return pHead;
vector flag;
int le=0;
while(n!=NULL){
if(flag.size()==0){
flag.push_back(1);
flag.push_back(1);
}else flag.push_back(1);
le++;
if(pHead->val == n->val){
flag[le]++;
flag[le-1]++;
}
pHead = pHead->next;
if(pHead!=NULL) {
n = pHead->next;
}
else n=pHead;
}
for(int i = 0 ; inext;
}
if(r==NULL) {
return r;}
pHead = r;
n = r->next;
while(n!=NULL){
if(flag[le]>1)
{
n=n->next;
le++;
if(n==NULL) {pHead->next = n;}
continue;
}
pHead->next = n;
pHead = pHead->next;
le++;
if(pHead!=NULL) {n=pHead->next;}
else n=pHead;
}
return r;
}
结果1:
通过。多种情况需要考虑,而且不能越界。
想法2:
看看讨论中的。递归。
代码2:
ListNode* deleteDuplication(ListNode* pHead)
{
if (pHead==NULL)
return NULL;
if (pHead!=NULL && pHead->next==NULL)
return pHead;
ListNode* current;
if ( pHead->next->val==pHead->val){ //如果当前和下一个重复,直接找到不重复为止
current=pHead->next->next;
while (current != NULL && current->val==pHead->val)
current=current->next;
return deleteDuplication(current);
}
else { //如果当前和下一个不重复,判断下一个,当前加入。
current=pHead->next;
pHead->next=deleteDuplication(current);
return pHead;
}
}
二叉树的下一个结点
题目:给定一个二叉树和其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针。
想法1:弄个中序遍历的数组,然后找出给定节点,输出下一个节点
代码1:
vector result;
void zhong(TreeLinkNode* pNode){
if(pNode != NULL){
zhong(pNode->left);
result.push_back(*pNode);
zhong(pNode->right);
}
}
TreeLinkNode* GetNext(TreeLinkNode* pNode)
{
TreeLinkNode* r = pNode;
while(pNode->next!=NULL){
pNode=pNode->next;
}
zhong(pNode);
for(int i =0;ival&&result[i].left == r->left&&result[i].right == r->right&&i!=result.size()-1){
r = &result[i+1];
return r;
}
}
return NULL;
}
结果1:
通过,看看讨论。
想法2:
对称的二叉树
题目:请实现一个函数,用来判断一颗二叉树是不是对称的。注意,如果一个二叉树同此二叉树的镜像是同样的,定义其为对称的。
想法1:中序遍历左右对称。
代码1:
vector result;
void zhong(TreeNode* pNode){
if(pNode != NULL){
zhong(pNode->left);
result.push_back(*pNode);
zhong(pNode->right);
}
}
bool isSymmetrical(TreeNode* pRoot)
{
if(pRoot==NULL) return true;
int f=0;
TreeNode* r = pRoot;
zhong(pRoot);
for(int i =f;ival&&result[i].left == r->left&&result[i].right == r->right){
f = i;
break;
}
}
if(result.size()-1-f!=f) return false;
for(int i =f;i=0){
if(result[i].val == result[f-(i-f)].val){
// cout< 结果1:
不通过,无法判断数值一样的错误树。比如:
{5,5,5,5,#,#,5,5,#,5}
想法2:
/*思路:首先根节点以及其左右子树,左子树的左子树和右子树的右子树相同
- 左子树的右子树和右子树的左子树相同即可,采用递归
- 非递归也可,采用栈或队列存取各级子树根节点
*/
代码2:
bool compare(TreeNode* le,TreeNode* ri){
if(le==NULL&&ri!=NULL) return false;
if(le!=NULL&&ri==NULL) return false;
if(le==NULL&&ri==NULL) return true;
if(le->val!=ri->val) return false;
return compare(le->left,ri->right)&&compare(le->right,ri->left);
}
bool isSymmetrical(TreeNode* pRoot)
{
if(pRoot == NULL){
return true;
}
return compare(pRoot->left, pRoot->right);
}
按之字形顺序打印二叉树
题目:请实现一个函数按照之字形打印二叉树,即第一行按照从左到右的顺序打印,第二层按照从右至左的顺序打印,第三行按照从左到右的顺序打印,其他行以此类推。
想法1:BFS,标志位设置正逆序,stack来辅助逆序。
代码1:
vector > Print(TreeNode* pRoot) {
bool flag = true;
queue le;
vector > result;
if(pRoot==NULL) return result;
le.push(*pRoot);
while(!le.empty()){
vector r;
stack ri;
for(int i =0,n=le.size();i 结果1:
通过,看看别人的。
想法2:
两个stack,奇数偶数。
public static ArrayList> Print(TreeNode pRoot) {
int layer = 1;
//s1存奇数层节点
Stack s1 = new Stack();
s1.push(pRoot);
//s2存偶数层节点
Stack s2 = new Stack();
ArrayList> list = new ArrayList>();
while (!s1.empty() || !s2.empty()) {
if (layer%2 != 0) {
ArrayList temp = new ArrayList();
while (!s1.empty()) {
TreeNode node = s1.pop();
if(node != null) {
temp.add(node.val);
System.out.print(node.val + " ");
s2.push(node.left);
s2.push(node.right);
}
}
if (!temp.isEmpty()) {
list.add(temp);
layer++;
System.out.println();
}
} else {
ArrayList temp = new ArrayList();
while (!s2.empty()) {
TreeNode node = s2.pop();
if(node != null) {
temp.add(node.val);
System.out.print(node.val + " ");
s1.push(node.right);
s1.push(node.left);
}
}
if (!temp.isEmpty()) {
list.add(temp);
layer++;
System.out.println();
}
}
}
return list;
把二叉树打印成多行
题目:从上到下按层打印二叉树,同一层结点从左至右输出。每一层输出一行。
想法1:
BFS
代码1:
vector > Print(TreeNode* pRoot) {
queue le;
vector > result;
if(pRoot==NULL) return result;
le.push(*pRoot);
while(!le.empty()){
vector r;
for(int i =0,n=le.size();i 结果1:
看看别人的。
想法2:
递归版本:
public class Solution {
ArrayList > Print(TreeNode pRoot) {
ArrayList> list = new ArrayList<>();
depth(pRoot, 1, list);
return list;
}
private void depth(TreeNode root, int depth, ArrayList> list) {
if(root == null) return;
if(depth > list.size())
list.add(new ArrayList());
list.get(depth -1).add(root.val);
depth(root.left, depth + 1, list);
depth(root.right, depth + 1, list);
}
}