121. Best Time to Buy and Sell Stock
problem:
Say you have an array for which the ith element is the price of a given stock on day i.
If you were only permitted to complete at most one transaction (ie, buy one and sell one share of the stock), design an algorithm to find the maximum prof
Input: [7, 1, 5, 3, 6, 4]
Output: 5
max. difference = 6-1 = 5 (not 7-1 = 6, as selling price needs to be larger than buying price)
thingking:
可以把这个问题想象的非常简单,简单地用数学语言描述就是:
If max{aj-ai }(j>i) > 0:
Return max{aj - ai }
Else return 0
其实这不够简单。这样来想: 把股票的波动看做是一个二维平面上连绵起伏的高山。你只能从左到右向上爬。这个问题中,你只有一次选择爬山起始点的机会,这个问题就可以归结为:怎么样才能使你一次爬山的相对海拔最高。
最价格数组进行扫描,每一次考察一个点a[i],我都去看看prices[0:i]中最矮的点海拔是多少(就成为valley吧)max{a[i] -valley} i = 1 to (len(prices) - 1 ) 就是最大的相对海拔。
Code:
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
# dp[i] is the min element in prices[0:i]
if len(prices) == 0:
return 0
dp = list(prices)
max_dis = -1
size = len(prices)
for i in range(1,size):
if dp[i] < dp[i-1]:
pass
else:
dp[i] = dp[i-1]
if prices[i] - dp[i-1] > max_dis:
max_dis = prices[i] - dp[i-1]
if max_dis <= 0 :
return 0
else:
return max_dis
122. Best Time to Buy and Sell Stock II
Say you have an array for which the ith element is the price of a given stock on day i.
Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times). However, you may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
Thinking:
相对于上面的问题,这个问题事实上就是: 你可以买多次,但是你的手中每次最多只能有一只股票。
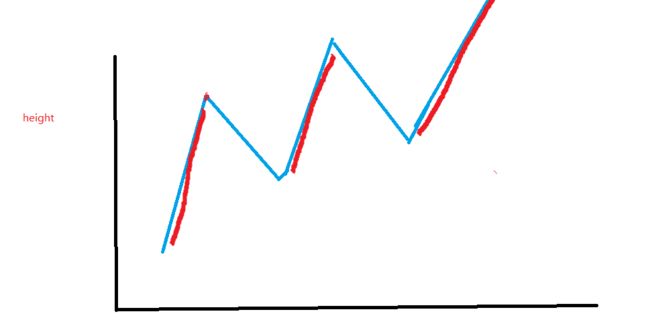
这个问题同样可以用爬山问题进行类比。有一片二维平面中高低起伏的山脉,你只能从左到右爬。当你爬到一个顶点之后。你可以在你的右侧的山脉中选择一个点继续往上爬。。直到山脉的尽头。求: 总共爬山高度的最大值。
考察每一个点的时候,如果这个点是山顶,减去左侧山谷的高度,加到最后值中,山顶变山谷,往后移动(山谷不是一成不变的,山谷必须是上次爬到的山顶之后的山谷)
简单地说就是把这样图形的红色部分的相对高度加总
Code:
class Solution(object):
def isPeak(self, li, pos):
flag = True
size = len(li)
if pos < 1 or size < 1:
flag = False
elif pos == size - 1 and li[pos] > li[pos - 1]:
flag = True
elif li[pos] > li[pos-1] and li[pos] >= li[pos + 1]:
flag = True
return flag
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
size = len(prices)
if size == 0:
return 0
valley = prices[0]
max_profit = 0
for i in xrange(1,size):
if prices[i] < vally:
valley = prices[i]
if self.isPeak(prices, i):
max_profit += (prices[i] - valley)
valley = prices[i]
return max_profit
123 Best Time to Buy and Sell Stock III
Leetcode 123
这才是boss 题,题目的难度比前面两道题大的多。题目的意思就是,你最多可以买两支股票,但是你的手上每一时刻最多只能持有一支股票,你该怎么买,才能使得收益最大?
Thinking
就像第一题中分析的那样,找到一支收益最大的股票非常容易,买两支股票收益最大化,一定会和收益最大的那支股票相关:
如果收益最大的一支股票出现在prices[left, right]这个区间,即prices[right] - prices[left]是最大的一笔收入
这样进行记录:
[ans,left,right] = maxSingeleProfit(prices)
# 这个函数就是表示在prices这个数据下最大的单笔股票交易收入
那么两只股票的最大收入就有三种可能:
[ans, left, right] = maxSingleProfit(prices)
# 1 left 买,right时卖, 又在买这个股票之前买了一笔
max1 = ans + maxSingleProfit(prices[:left])
# 2 left 买,right时卖 , 又在卖这个股票之后买了一笔
max2 = ans + maxSingleProfit(prices[right+1 : ])
# left处买,中间卖了一次,又在某一天买了,最后在right 又卖了这支股票
max3 = twoStepBuy(prices[left:right+1])
real_max = max(max1, max2, max3)
Codes
class Solution(object):
def maxSingleProfit(self, prices):
'''
:param prices:
:return: [ans, left, right]: buy at prices[left] and
sell at prices[right] we can get maxSingleProfit ans.
'''
size = len(prices)
left = 0
right = size - 1
if size <= 1:
return [0, 0, 0]
valley = prices[0]
valley_index = 0
ans = 0
for i in xrange(1, size):
if prices[i] < valley:
valley = prices[i]
valley_index = i
if prices[i] - valley > ans:
ans = prices[i] - valley
right = i
left = valley_index
return [ans, left, right]
def Peaks(self,prices):
size = len(prices)
if size <= 1:
return []
ans = []
for i in range(1, size - 1):
if prices[i] > prices[i-1] and prices[i] >= prices[i+1]:
ans.append(i)
return ans
def twoStepBuy(self,prices):
size = len(prices)
if size <= 2:
return 0
peaks = self.Peaks(prices)
left = 0
right = len(prices) - 1
max_profit = prices[right] - prices[left]
for peak_id in peaks:
tmp = self.maxSingleProfit(prices[peak_id:])[0]
if ((prices[peak_id] - prices[0]) + tmp) > max_profit:
max_profit = (prices[peak_id] - prices[0]) + tmp
return max_profit
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
size = len(prices)
if size < 0:
return 0
tmp = self.maxSingleProfit(prices)
max_one = tmp[0]
left = tmp[1]
right = tmp[2]
max_two = max_one + max(self.maxSingleProfit(prices[0:left])[0], self.maxSingleProfit(prices[right + 1:])[0])
return max(max_two, self.twoStepBuy(prices[left:right+1]))