- 集合 Set
- 基于二分搜索树实现集合
- 基于链表实现集合
- 集合的时间复杂度分析
- 映射 Map
- 基于链表实现映射
- 基于二分搜索树实现映射
- 映射的时间复杂度分析
- leetcode上关于集合和映射的问题
集合 Set
Set是一种新的数据结构,类似于数组,但是不能添加重复的元素,基于Set集合的这个特性,我们可以使用Set集合进行客户统计和词汇统计等,集合中常用的方法如下:
public interface Set {
void add(E e); //添加元素e,不能添加重复元素
boolean contains(E e); //当前集合中是否包含元素e
void remove(E e); //删除元素e
int getSize(); //获取当前集合中元素的个数
boolean isEmpty(); //判断当前集合是否为空
}
基于二分搜索树实现集合
现在让我们基于我们上章实现的二分搜索树,来实现集合中的常用操作,若你对二分搜索树还不了解,你可以先看我的上一篇文章:二分搜索树(Binary Search Tree)进行学习,基于二分搜索树实现的集合代码实现如下:
public class BSTSet> implements Set {
//基于二分搜索树实现集合
private BST bst;
public BSTSet(){
bst = new BST();
}
//直接调用bst的添加方法
@Override
public void add(E e) {
bst.add(e);
}
@Override
public boolean contains(E e) {
return bst.contains(e);
}
@Override
public void remove(E e) {
bst.removeElement(e);
}
@Override
public int getSize() {
return bst.getSize();
}
@Override
public boolean isEmpty() {
return bst.isEmpty();
}
}
现在让我们使用该集合实现对词数的统计,我们可以写一个简单的测试类,来实现分别对《傲慢与偏见》和《双城记》这两本书中不同单词的统计,这两本书英文版的下载链接:https://files.cnblogs.com/files/reminis/test-text.zip , 在使用我们的集合类进行词数统计之前,我们需要先写一个读取文件的工具类,该文件操作工具类可以实现读取文件中的内容,并将其中包含的所有词语放进words中,具体实现代码如下:
import java.io.FileInputStream;
import java.util.ArrayList;
import java.util.Scanner;
import java.util.Locale;
import java.io.File;
import java.io.BufferedInputStream;
import java.io.IOException;
// 文件相关操作
public class FileOperation {
// 读取文件名称为filename中的内容,并将其中包含的所有词语放进words中
public static boolean readFile(String filename, List words){
if (filename == null || words == null){
System.out.println("filename is null or words is null");
return false;
}
// 文件读取
Scanner scanner;
try {
File file = new File(filename);
if(file.exists()){
FileInputStream fis = new FileInputStream(file);
scanner = new Scanner(new BufferedInputStream(fis), "UTF-8");
scanner.useLocale(Locale.ENGLISH);
}
else
return false;
}
catch(IOException ioe){
System.out.println("Cannot open " + filename);
return false;
}
// 简单分词
// 这个分词方式相对简陋, 没有考虑很多文本处理中的特殊问题
// 在这里只做demo展示用
if (scanner.hasNextLine()) {
String contents = scanner.useDelimiter("\\A").next();
int start = firstCharacterIndex(contents, 0);
for (int i = start + 1; i <= contents.length(); )
if (i == contents.length() || !Character.isLetter(contents.charAt(i))) {
String word = contents.substring(start, i).toLowerCase();
words.add(word);
start = firstCharacterIndex(contents, i);
i = start + 1;
} else
i++;
}
return true;
}
// 寻找字符串s中,从start的位置开始的第一个字母字符的位置
private static int firstCharacterIndex(String s, int start){
for( int i = start ; i < s.length() ; i ++ )
if( Character.isLetter(s.charAt(i)) )
return i;
return s.length();
}
}
大家如果不是很懂上面文件类中的代码,可以先直接拷贝在自己的项目中,直接进行使用就行了,因为本文主要是讲的集合,关于文件操作的知识不会涉及太多,下面让我们使用集合来进行词树统计操作,测试代码如下:
public static void main(String[] args) {
System.out.println("Pride and Prejudice");
List words1 = new ArrayList();
//注意自己文件的路径的问题
if(FileOperation.readFile("pride-and-prejudice.txt", words1)) {
//输出《傲慢与偏见》这本书中的总词数
System.out.println("Total words: " + words1.size());
BSTSet set1 = new BSTSet();
for (String word : words1) {
//将《傲慢与偏见》这本书中的所有单词加如我们的基于二分搜索树实现的集合中
set1.add(word);
}
//输出《傲慢与偏见》这本书中去重后的总词数
System.out.println("Total different words: " + set1.getSize());
}
System.out.println();
//测试《双城记》这本书
System.out.println("A Tale of Two Cities");
List words2 = new ArrayList();
//注意自己文件路径的问题
if(FileOperation.readFile("a-tale-of-two-cities.txt", words2)){
System.out.println("Total words: " + words2.size());
BSTSet set2 = new BSTSet();
for(String word: words2)
set2.add(word);
System.out.println("Total different words: " + set2.getSize());
}
}
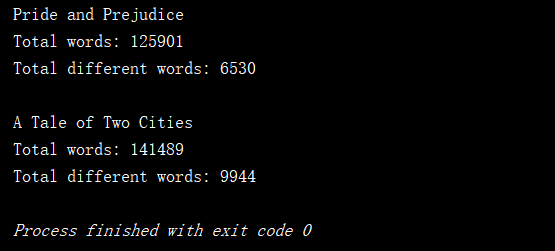
测试代码的运行结果如下:

注意:在本次测试中,只是进行简单的分词,对单词的不同形式未进行处理(例如同一个单词的不同时态是作为不同的单词在进行处理)。
基于链表实现集合
由于我们在常见的线性结构中讲过链表,为了与基于二分搜索实现的集合进行对比,我们也可以基于链表来实现集合,也顺便复习一下链表的相关操作,基于链表实现集合的具体代码如下:
public class LinkedListSet implements Set {
//基于链表实现
private LinkedList linkedList;
public LinkedListSet(){
linkedList = new LinkedList();
}
//由于链表中的添加操作是可以添加重复元素的
//所以这里向集合中添加元素时,需要先判断集合中是否有该元素
@Override
public void add(E e) {
if ( !linkedList.contains(e))
linkedList.addFirst(e);
}
@Override
public boolean contains(E e) {
return linkedList.contains(e);
}
@Override
public void remove(E e) {
linkedList.removeElement(e);
}
@Override
public int getSize() {
return linkedList.getSize();
}
@Override
public boolean isEmpty() {
return linkedList.isEmpty();
}
}
现在我们再来使用基于链表实现的集合来进行词数统计操作,与上面的测试代码一样,只不过将BSTSet改为LinkedListSet,如下:
public static void main(String[] args) {
System.out.println("Pride and Prejudice");
List words1 = new ArrayList();
if(FileOperation.readFile("pride-and-prejudice.txt", words1)) {
System.out.println("Total words: " + words1.size());
LinkedListSet set1 = new LinkedListSet();
for (String word : words1)
set1.add(word);
System.out.println("Total different words: " + set1.getSize());
}
System.out.println();
System.out.println("A Tale of Two Cities");
ArrayList words2 = new ArrayList();
if(FileOperation.readFile("a-tale-of-two-cities.txt", words2)){
System.out.println("Total words: " + words2.size());
LinkedListSet set2 = new LinkedListSet();
for(String word: words2)
set2.add(word);
System.out.println("Total different words: " + set2.getSize());
}
}
集合的时间复杂度分析
现在先让我们使用基于二分搜索数实现的集合与基于链表实现的集合,都对《傲慢与偏见》这本书进行词数统计,让我们对比一下运行所需要花费的时间,测试如下:
/**
* 该集合对指定文件进行添加操作所需要花费的时间
* @param set 集合
* @param filename 文件名
* @return
*/
private static double testSet(Set set, String filename){
long startTime = System.nanoTime();
System.out.println(filename);
List words = new ArrayList();
if(FileOperation.readFile(filename, words)) {
System.out.println("Total words: " + words.size());
for (String word : words)
set.add(word);
System.out.println("Total different words: " + set.getSize());
}
long endTime = System.nanoTime();
//将纳秒转为秒
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
String filename = "pride-and-prejudice.txt";
Set bstSet = new BSTSet();
//基于二分搜索树实现的集合进行测试
double time1 = testSet(bstSet, filename);
System.out.println("BST Set: " + time1 + " s");
System.out.println();
Set linkedListSet = new LinkedListSet();
//基于链表实现的集合进行测试
double time2 = testSet(linkedListSet, filename);
System.out.println("Linked List Set: " + time2 + " s");
}
测试代码运行结果如下:
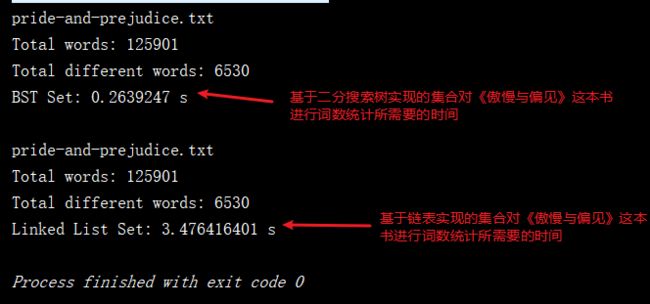
从运行结果可以看出,两种不同的实现性能上的差异是非常大的,现在就让我们来对比下二者的时间复杂度:
| LinkedListSet | BSTSet | |
|---|---|---|
| 增 add | O(n) | O(h) |
| 查 contains | O(n) | O(h) |
| 删 remove | O(n) | O(h) |
这里的n是指节点的个数,链表的add()方法的时间复杂度是O(1)级别的,为什么这里LinkedListSet的时间复杂度为O(n)呢,因为Set集合中不允许添加重复的元素,所以在基于链表实现的集合中,我们每次添加元素时都会先遍历这个链表,看这个链表中是否有这个元素,没有才进行添加,这就让我们的LinkedListSet添加一个元素所需要的时间与链表中节点的个数n呈线性关系,即时间复杂度为O(n)级别的。而基于二分搜索树实现的集合,增删查的时间复杂度都为O(h),这里的h是指树的高度,即BSTSet的这些操作都只和这棵二分搜索树的高度相关。但我们的时间复杂度是研究的和节点个数n的关系,所以下面让我们来看一下二分搜索树的高度h和节点个数n之间的关系。
特殊情况:当我们的二分搜索树为满二叉树时,来进行分析二分搜索树的高度和节点个数之间的关系。满二叉树就是除了叶子节点外,其他每个节点的左孩子和右孩子都不为空。一棵满的二叉树并且是二分搜索树如下图:
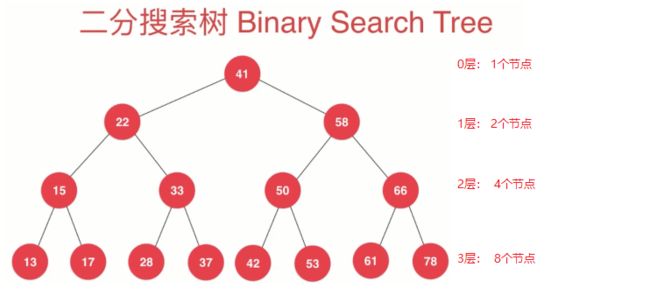
我们可以从图中发现高度和节点个数有如下关系:
| 层数 | 节点个数 | 关系 |
|---|---|---|
| 0层 | 1个节点 | 20 |
| 1层 | 2个节点 | 21 |
| 2层 | 4个节点 | 22 |
| 3层 | 8个节点 | 23 |
| 4层 | 16个节点 | 24 |
| ... | ... | ... |
| h-1层 | 2(h-1) | 2(h-1) |
所以在h层,一共有多少个节点呢?相信大家都已经学过高中数学的等比数列,我们通过我们推导出的通项公式,可以知道这是一个以2为底,以2为公比的等比数列,所以在第h层的节点个数推导如下:
所以二分搜索数高度h和节点个数n的关系是:\(h=log_2(n+1)\),所以二分搜索树的复杂为:\(O(h)=O(log_2 n)=O(log n)\)
下面我们看一下O(log n)复杂度和O(n)复杂度之间的差距(这里就把log的底看为2进行对比):
| 节点个数 | log n | n | 执行时间差别 |
|---|---|---|---|
| n=16 | 4 | 16 | 相差4倍 |
| n=1024 | 10 | 1024 | 相差100倍 |
| n=100万 | 20 | 100万 | 相差5万倍 |
由上面的对比我们可以看出,时间复杂度为O(log n)的程序运行时间要比时间复杂度为O(n)的程序快很多,特别是在进行大数据量处理时,差别效果是很明显的。这也是为什么基于二分搜索树实现的集合要比基于链表实现的集合在执行相同操作时用时更少了。
注意:上面我们是根据二分搜索树是满二叉树的情况下推导出来的时间复杂度为O(logn),但当我们向二分搜索树中按顺序添加这些数据时,二分搜索树就会退化成一个链表,这时我们的二分搜索树的时间复杂度就为log(n)了,因为此时数的高度就为链表的长度了,即等于链表中节点的个数。
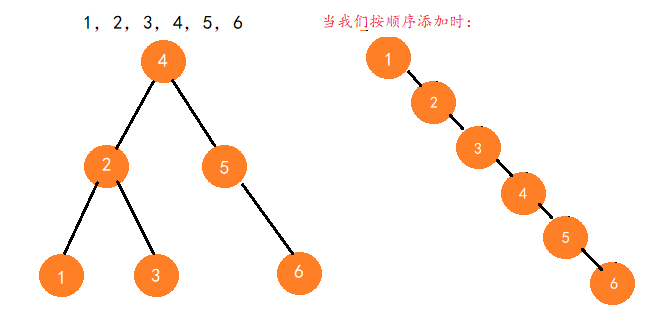
所以两种实现的集合的时间复杂度分析如下:
| LinkedListSet | BSTSet | 平均 | 最差 | |
|---|---|---|---|---|
| 增 add | O(n) | O(h) | O(logn) | O(n) |
| 查 contains | O(n) | O(h) | O(logn) | O(n) |
| 删 remove | O(n) | O(h) | O(logn) | O(n) |
下面让我们来通过leetcode上的804号练习题关于唯一摩尔斯密码词问题,来对集合这种数据结构进行运用:

上面是关于804号问题描述的部分截图,建议大家去看leetcode官网上看该问题的完整要求,现在就让我们来使用基于二分搜索树实现的集合来解决该问题:
public int uniqueMorseRepresentations(String[] words) {
//a~z的摩斯密码
String[] codes = {".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."};
BSTSet set = new BSTSet();
for(String word: words){
StringBuilder res = new StringBuilder();
for(int i = 0 ; i < word.length() ; i ++){
//因为题目描述中每个单词 words[i]只包含小写字母
//我们需要减去a对应ASCII码的偏移量,就可以获的对应字符的摩斯密码
res.append(codes[word.charAt(i) - 'a']);
}
//因为set集合中不能添加重复元素,所以我们的集合中不会有重复的单词
set.add(res.toString());
}
return set.getSize();
}
你也可以使用我们上面基于链表实现的集合,当你使用基于我们自己实现的集合,提交代码到leetcode上时,你需要把我们自己实现的集合作为私有类一起提交到leetcode上,不然会报错,当然你也可以使用Java类库中的TreeSet来解决这个问题。
映射 Map
Map是一种用来存储(键,值)数据对的数据结构(key,value);根据键(key)寻找值(value),非常容易使用链表或者二分搜索树来实现,当然Map中的key是不允许重复的。Map接口中常用的操作如下:
/**
* 定义Map接口,由于Map是用来存储数据对的数据结构,所以定义时需要两个泛型
* @param 键的类型使用泛型代替
* @param 值的类型使用泛型代替
*/
public interface Map {
//添加一个数据对
void add(K key, V value);
//根据键来删除这个数据对,并且返回删除的值
V remove(K key);
//查找这个map中是否包含key
boolean contains(K key);
//通过键查找这个数据对的值
V get(K key);
//修改
void set(K key, V newValue);
//获取当前映射中数据对的个数
int getSize();
//判断当前映射是否为空
boolean isEmpty();
}
基于链表实现映射
我们在之前实现的链表中的节点,只包含一个数据E,由于这里Map是存储的一个数据对,所以我们我们链表中的节点需要存储两个数据,分别是key和value。具体代码实现如下:
public class LinkedListMap implements Map {
//定义链表的节点
private class Node{
//存储Map的键值对
public K key;
public V value;
//指向像下一个节点
public Node next;
//链表节点的有参构造
public Node(K key, V value, Node next) {
this.key = key;
this.value = value;
this.next = next;
}
//当用户在创建节点时,上传了key和value的初始值
public Node(K key, V value){
this(key, value, null);
}
//链表节点的无参构造
public Node(){
this(null, null, null);
}
//键和值的输出格式为: key:value
@Override
public String toString(){
return key.toString() + " : " + value.toString();
}
}
//虚拟头节点(不存储数据)
private Node dummyHead;
private int size;
//Map的无参构造
public LinkedListMap(){
dummyHead = new Node();
size = 0;
}
@Override
public int getSize() {
return size;
}
@Override
public boolean isEmpty() {
return size==0;
}
//根据key所在的节点,Map中的key是唯一的
private Node getNode(K key){
Node cur = dummyHead.next;
while (cur != null){
if (cur.key.equals(key)){
return cur;
}
cur = cur.next;
}
return null;
}
@Override
public boolean contains(K key) {
//若根据key找到了对应的节点,则该Map中含有该键
return getNode(key) != null;
}
@Override
public V get(K key) {
Node node = getNode(key);
return node == null ? null : node.value;
}
@Override
public void add(K key, V value) {
//添加之前,先查找该映射中key是否已经存在了
Node node = getNode(key);
if (node == null){
dummyHead.next = new Node(key,value,dummyHead.next);
size ++;
}else {
//如果该节点已存在,则覆盖值
node.value =value;
}
}
@Override
public void set(K key, V newValue) {
Node node = getNode(key);
//在进行修改操作时,如果该节点不存在,则抛出异常
if(node == null)
throw new IllegalArgumentException(key + " doesn't exist!");
node.value = newValue;
}
@Override
public V remove(K key) {
Node prev = dummyHead;
while (prev.next != null){
if (prev.next.key.equals(key)){
break;
}
prev = prev.next;
}
//prev.next 就是需要删除的节点
if (prev.next != null){
Node delNode = prev.next;
prev.next = delNode.next;
delNode.next = null;
size --;
return delNode.value;
}
return null;
}
}
现在我们可以来简单测试一下我们使用链表实现的映射是否正确,测试用例还是和前面测试集合一样,来对《傲慢与偏见》这本书进行测试,这本书的文本下载链接在前面已经写出来了,现在就进行测试吧
public static void main(String[] args){
System.out.println("Pride and Prejudice");
List words = new ArrayList();
if(FileOperation.readFile("pride-and-prejudice.txt", words)) {
//《傲慢与偏见》这本书的总词数
System.out.println("Total words: " + words.size());
//让我们的映射中存储key,value分别表示单词和这个单词出现的次数
Map map = new LinkedListMap();
for (String word : words) {
//如果当前应次数已经存在这个单词(键)了,就让我们对这个次数进行加一
if (map.contains(word)){
map.set(word, map.get(word) + 1);
} else {
//如果该单词是第一次出现,频次就设置为一
map.add(word, 1);
}
}
//输出《傲慢与偏见》这本书不同单词的总数
System.out.println("Total different words: " + map.getSize());
//输出这本书中出“pride”这个单词的次数
System.out.println("Frequency of PRIDE: " + map.get("pride"));
//输出这本书中出“prejudice”这个单词的次数
System.out.println("Frequency of PREJUDICE: " + map.get("prejudice"));
}
System.out.println();
}
上面测试代码的运行结果如下:

说明:测试代码中文件操作类在对集合进行测试时,已经写出来了,这里的文件操作类是同一个类,直接使用即可。
基于二分搜索树实现映射
若你对二分搜索树的相关操作实现还不了解,建议你在看我的上篇博客二分搜索树后,在进行向下阅读,因为下面我实现的BSTMap是基于我之前写的二分搜索树来进行实现的,之前我们树节点中只存储了一个数据,现在我们需要同时存储键和值这种数据对,所以我们需要对树的节点做一些调整,具体实现如下:
/**
* 前面我们说过二分搜索树中元素必须具有可比较性,所以这里让Map的键实现Comparable接口
* @param
* @param
*/
public class BSTMap,V> implements Map {
//二分搜索树的节点
private class Node{
public K key;
public V value;
//左孩子和右孩子节点
public Node left,right;
public Node(K key, V value) {
this.key = key;
this.value = value;
this.left = null;
this.right = null;
}
}
//根节点
private Node root;
private int size;
//Map的无参构造
public BSTMap() {
this.root = null;
this.size = 0;
}
@Override
public int getSize() {
return size;
}
@Override
public boolean isEmpty() {
return size == 0;
}
@Override
public void add(K key, V value) {
// 向二分搜索树中添加新的元素(key, value)
root = add(root,key,value);
}
// 向以node为根的二分搜索树中插入元素(key, value),递归算法
// 返回插入新节点后二分搜索树的根
private Node add(Node node, K key, V value) {
if (node == null){
size ++;
return new Node(key,value);
}
if (key.compareTo(node.key) < 0){
node.left = add(node.left,key,value);
}else if (key.compareTo(node.key) > 0){
node.right = add(node.right,key,value);
}else { // key.compareTo(node.key) == 0
node.value = value;
}
return node;
}
// 返回以node为根节点的二分搜索树中,key所在的节点
public Node getNode(Node node,K key){
if (node == null)
return null;
if (key.equals(node.key)){
return node;
} else if (key.compareTo(node.key) < 0) {
return getNode(node.left,key);
}else { //key.compareTo(node.key) > 0
return getNode(node.right,key);
}
}
@Override
public boolean contains(K key) {
return getNode(root,key) != null;
}
@Override
public V get(K key) {
Node node = getNode(root, key);
return node == null ? null : node.value;
}
@Override
public void set(K key, V newValue) {
Node node = getNode(root, key);
if(node == null)
throw new IllegalArgumentException(key + " doesn't exist!");
node.value = newValue;
}
@Override
public V remove(K key) {
Node node = getNode(root, key);
if (node != null){
root = remove(root,key);
return root.value;
}
return null;
}
private Node remove(Node node, K key) {
if (node == null){
return null;
}
if (key.compareTo(node.key) <0 ){
node.left = remove(node.left,key);
return node;
}else if (key.compareTo(node.key) > 0){
node.right = remove(node.right,key);
return node;
}else { // key.compareTo(node.key) == 0
// 待删除节点左子树为空的情况
if (node.left == null){
Node rightNode = node.right;
node.right = null;
size -- ;
return rightNode;
}
//待删除节点右子树为空的情况
if (node.right == null){
Node leftNode = node.left;
node.left = null;
size -- ;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = minNum(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node) {
if (node.left == null){
Node rightNode = node.right;
node.right = null;
size -- ;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 返回以node为根的二分搜索树的最小值所在的节点
private Node minNum(Node node) {
if (node.left == null){
return node;
}
return minNum(node.left);
}
}
现在来对我们基于二分搜索树实现的映射进行测试,测试代码与基于链表实现的映射的测试代码相同,如下:
public static void main(String[] args){
System.out.println("Pride and Prejudice");
List words = new ArrayList();
if(FileOperation.readFile("pride-and-prejudice.txt", words)) {
System.out.println("Total words: " + words.size());
BSTMap map = new BSTMap();
for (String word : words) {
if (map.contains(word))
map.set(word, map.get(word) + 1);
else
map.add(word, 1);
}
System.out.println("Total different words: " + map.getSize());
System.out.println("Frequency of PRIDE: " + map.get("pride"));
System.out.println("Frequency of PREJUDICE: " + map.get("prejudice"));
}
System.out.println();
}
基于二分搜索树实现的映射的测试结果如下:

我们可以看到该测试结果和基于链表实现映射的测试结果是相同的,下面就让我们来对这两种实现的时间复杂度进行分析吧。
映射的时间复杂度分析
我们现在先来写一个程序,来测试这两种不同实现的映射运行所需要的时间,这段测试代码其实大家已经很熟悉了,和我们前面测试集合的运行时间代码是一样的,如下:
private static double testMap(Map map, String filename){
//获取当前系统的时间,单位时纳秒
long startTime = System.nanoTime();
System.out.println(filename);
List words = new ArrayList();
if(FileOperation.readFile(filename, words)) {
System.out.println("Total words: " + words.size());
for (String word : words){
if(map.contains(word))
map.set(word, map.get(word) + 1);
else
map.add(word, 1);
}
System.out.println("Total different words: " + map.getSize());
System.out.println("Frequency of PRIDE: " + map.get("pride"));
System.out.println("Frequency of PREJUDICE: " + map.get("prejudice"));
}
long endTime = System.nanoTime();
//将时间单位纳秒转为秒
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
String filename = "pride-and-prejudice.txt";
//基于二分搜索树实现的映射
Map bstMap = new BSTMap();
double time1 = testMap(bstMap, filename);
System.out.println("BST Map: " + time1 + " s");
System.out.println();
//基于链表实现的映射
Map linkedListMap = new LinkedListMap();
double time2 = testMap(linkedListMap, filename);
System.out.println("Linked List Map: " + time2 + " s");
}
测试代码的运行结果如下:

由于我们前面在集合中的学习可以知道,二分搜索树的增删改查的时间复杂度平均为O(logn),而链表的时间复杂度为O(n),如下:
| LinkedListMap | BSTMap | 平均 | 最差 | |
|---|---|---|---|---|
| 增 add | O(n) | O(h) | O(logn) | O(n) |
| 删 remove | O(n) | O(h) | O(logn) | O(n) |
| 改 set | O(n) | O(h) | O(logn) | O(n) |
| 查 get | O(n) | O(h) | O(logn) | O(n) |
| 查 contains | O(n) | O(h) | O(logn) | O(n) |
其实通过集合和映射的学习我们可以发现,由于集合种元素也是不允许重复的,和映射种键的唯一性是一样的,所以我们完全可以基于集合,来实现映射,当然也可以基于映射的键,来实现集合。
leetcode上关于集合和映射的问题
349号问题:两个数组的交集
问题:给定两个数组,编写一个函数来计算它们的交集。该题的详细题目描述请上leetcode搜索题号进行查看!
思路:先定义一个动态数组ArrayList,用来存储两个数组的交集元素,我们可以把其中一个数组的所有元素加入Set集合中,然后再对另外一个数组进行遍历,判断Set中是否有该元素,如已经存在,则把该元素加入动态数组ArrayList中,代码实现如下:
public int[] intersection(int[] nums1, int[] nums2) {
//这里是使用的Java类库中的TreeSet,我们也可以使用我们自己基于二分搜索树是实现的Set
TreeSet set = new TreeSet();
for (int num : nums1) {
set.add(num);
}
List list = new ArrayList();
for (int num : nums2) {
if (set.contains(num)){
list.add(num);
//从set集合删除该元素,为了避免下次运到该元素进行重复添加
set.remove(num);
}
}
//返回值需要一个数组
int[] res = new int[list.size()];
for (int i=0; i 350号问题:两个数组的交集II
题目要求:输出结果中每个元素出现的次数,应与元素在两个数组中出现的次数一致。
说明:该题的详细题目描述请上leetcode搜索题号进行查看!
仔细审题后,我们会发现对比于349题,多了应与元素在两个数组中出现的次数一致的这个要求,我们可以对数组中交集元素的出现次数进行统计,即可以采用 映射这中数据结构,具体实现如下:
public int[] intersect(int[] nums1, int[] nums2) {
//key-代表数组中的元素,value表示的是该元素出现的次数
//这里我们使用的是Java类库提供的TreeMap,你也可以使用我们基于二分搜索树实现的Map来解决这个问题
Map map = new TreeMap();
for (int num : nums1) {
if (map.containsKey(num)){
map.put(num,map.get(num)+1);
}else {
map.put(num,1);
}
}
//用来存储包含重复元素的集合
List res = new ArrayList();
for(int num: nums2){
if(map.containsKey(num)){
res.add(num);
map.put(num, map.get(num) - 1);
if(map.get(num) == 0)
map.remove(num);
}
}
int[] ret = new int[res.size()];
for(int i = 0 ; i < res.size() ; i ++)
ret[i] = res.get(i);
return ret;
}