Android Interpolator解析

本文部分图片转自：https://blog.csdn.net/lgaojiantong/article/details/39451243

目录

1. 自定义插值器
2. 系统插值器

1. 自定义插值器

要自定义插值器，首先得看看系统的插值器是怎么写的。这里从最简单的LinearInterpolator入手，查看其继承关系：

public class LinearInterpolator extends BaseInterpolator implements NativeInterpolatorFactory {

    public LinearInterpolator() {
    }

    public LinearInterpolator(Context context, AttributeSet attrs) {
    }

    public float getInterpolation(float input) {
        return input;
    }

    /** @hide */
    @Override
    public long createNativeInterpolator() {
        return NativeInterpolatorFactoryHelper.createLinearInterpolator();
    }
}

可以看到，LinearInterpolator继承自BaseInterpolator。一路往上，发现BaseInterpolator实现了Interpolator接口，而Interpolator则继承于TimeInterpolator。终于到了源头，现在来看看TimeInterpolator的源码：

public interface TimeInterpolator {
    float getInterpolation(float input);
}

TimeInterpolator的代码特别简单，只有一个getInterpolation()方法，这就是插值器的核心所在。参数input代表动画的进度，范围是从0到1.0，当input为1.0时，则动画结束。需要注意的是，我们定义的任何值，都不会对此参数造成影响。而getInterpolation()的返回值，则是我们所需要的插值，范围也是从0到1.0，但根据需要可以返回小于0或大于1.0的数值，分别表示起点往回以及超出终点（用英文中的undershoot和overshoot可能更方便理解）。

理解了上述内容后，现在来写一个简单的自定义Interpolator：

public class MyInterpolator implements TimeInterpolator {
    @Override
    public float getInterpolation(float input) {
        return 1-input;
    }
}

这个插值器的效果是起点和终点倒转过来。

2. 系统插值器

（1）LinearInterpolator：

public float getInterpolation(float input) {
    return input;
}

y=x，直接把input的值返回，增量为常量，呈线性增长。

（2）AccelerateDecelerateInterpolator：

public float getInterpolation(float input) {
    return (float)(Math.cos((input + 1) * Math.PI) / 2.0f) + 0.5f;
}

余弦函数的半个周期，起点和终点增长缓慢，而中间快速增长。

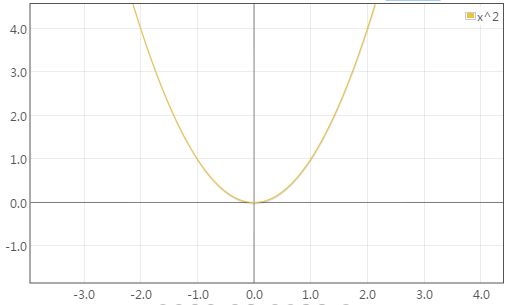
（3）AccelerateInterpolator：

public float getInterpolation(float input) {
    if (mFactor == 1.0f) {
        return input * input;
    } else {
        return (float)Math.pow(input, mDoubleFactor);
    }
}

返回input的n次幂，即抛物线的右半部分，起点缓慢，然后加速。

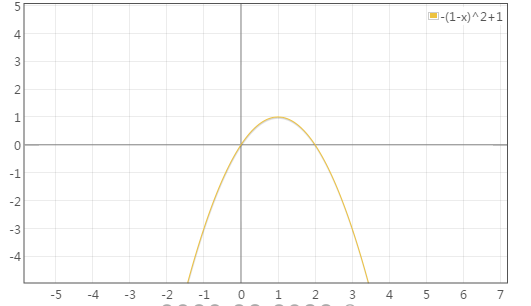
（4）DecelerateInterpolator：

public float getInterpolation(float input) {
    float result;
    if (mFactor == 1.0f) {
        result = (float)(1.0f - (1.0f - input) * (1.0f - input));
    } else {
        result = (float)(1.0f - Math.pow((1.0f - input), 2 * mFactor));
    }
    return result;
}

开口向下的抛物线，input是从0到1，可以看到下图0到1的那一段，起点快速增长，而后逐渐减慢。

（5）AnticipateInterpolator：

public float getInterpolation(float t) {
    return t * t * ((mTension + 1) * t - mTension);
}

mTension默认值为2，因此下图也是按照mTension为2来绘制的。起点的时候回往回一定值，而后再往前。

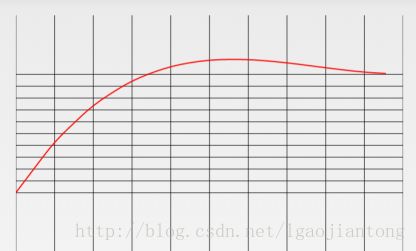
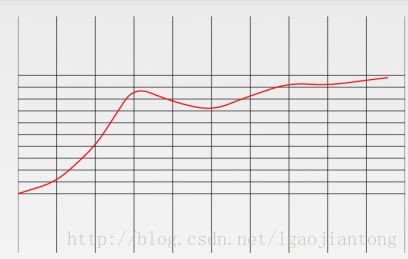
（6）OvershootInterpolator：

public float getInterpolation(float t) {
    t -= 1.0f;
    return t * t * ((mTension + 1) * t + mTension) + 1.0f;
}

这个用绘图工具不知道怎么画，引用一下别人的图。大概感觉就是这样，到终点后超出一定值，然后再返回。

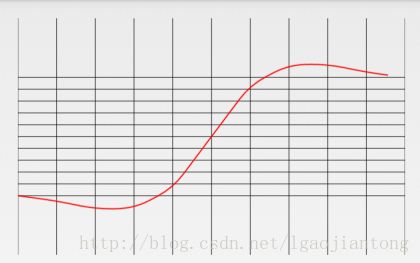
（7）AnticipateOvershootInterpolator：

private static float a(float t, float s) {
    return t * t * ((s + 1) * t - s);
}

private static float o(float t, float s) {
    return t * t * ((s + 1) * t + s);
}

public float getInterpolation(float t) {
    if (t < 0.5f) 
        return 0.5f * a(t * 2.0f, mTension);
    else 
        return 0.5f * (o(t * 2.0f - 2.0f, mTension) + 2.0f);
}

起点往回一定值，然后往前，到终点再超出一定值，然后返回。

（8）BounceInterpolator：

private static float bounce(float t) {
    return t * t * 8.0f;
}

public float getInterpolation(float t) {
    t *= 1.1226f;
    if (t < 0.3535f) 
        return bounce(t);
    else if (t < 0.7408f) 
        return bounce(t - 0.54719f) + 0.7f;
    else if (t < 0.9644f)
        return bounce(t - 0.8526f) + 0.9f;
    else
        return bounce(t - 1.0435f) + 0.95f;
}

类似于球掉落地面的效果。

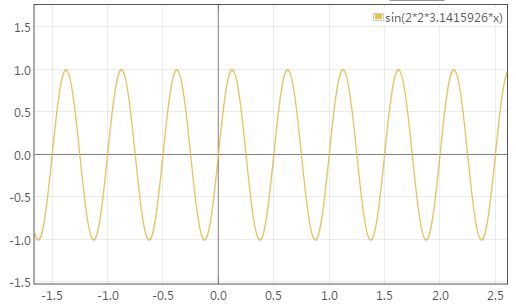
（9）CycleInterpolator：

public float getInterpolation(float input) {
    return (float)(Math.sin(2 * mCycles * Math.PI * input));
}

正弦曲线， 循环播放mCycles次。例如下图中，mCycles取值为2，那么在0到1这个区间内，函数有2个周期，也就是动画播放2次。