墙角数枝梅,凌寒独自开。
遥知不是雪,为有暗香来。——王安石
题目:天气预报
网址:http://poj.org/problem?id=2044
你是一个可以控制降雨的神仙。
你是一个仁慈的神,希望土地在平时可以有足够的雨水,在赶集和过节能够充满阳光。
你负责掌控一个村子的天气状况。
这个村子呈4 x 4的网格状分布,村子内的每个区域被编号如下图所示:
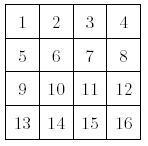
你拥有一片2 x 2大小的云,这片云不能到村子以外的地方。
你将获得一段时间内村子每个区域的赶集和过节时间表。
在这段时间的第一天,中部地区(6-7-10-11)将会下雨。
在接下来的每一天中,您可以在四个基本方向(东南西北)之中选取一个方向,将云移动1或2个方格,或将其保持在相同位置。
不允许对角线移动。
任何地区都不能连续七天或以上时间都不降雨。
这段时间以外的日子的下雨状况你无需做任何考虑。
输入格式
输入包含多组测试用例。
对于每组测试用例,第一行包含一个整数N,表示这段时间的具体天数。
接下里N行,描绘了接下来N天的赶集和过节时间表,第i行表示第i天的时间表。
这N行里,每行包含16个数字(0或1),0表示正常的一天,1表示赶集和过节的一天,第i个数字表示第i个区域的具体情况。
每行数字之间用空格隔开。
当输入测试用例N=0时,表示输入终止,且该用例无需处理。
输出格式
每个测试用例输出一个整数0或1,如果可以保证整个时间段内,该下雨的地方下雨,不该下的地方不下,则输出1。
如果不能保证则输出0,每个结果占一行。
数据范围
1≤N≤365
输入样例:
1
0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
7
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 1 0 0 0 0 1 1 0 0 1
0 0 0 0 0 0 0 0 1 0 0 0 0 1 0 1
0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0
0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0
1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0
7
0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0
0 0 0 1 0 0 0 0 0 0 1 0 1 0 0 0
0 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 0 1 0 0 0 0 1
0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
15
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 1 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
0 0 1 1 0 0 0 0 0 1 0 0 0 0 0 0
1 1 0 0 0 0 0 0 0 0 1 0 0 1 0 0
0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0
1 0 0 1 1 0 0 0 0 1 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 1 0 1 0 1 0 0 0 0 0 0
0
输出样例:
0
1
0
1
这道题其实细节上颇多。
首先,判断每个地区是否连续七天没有浇水,实际上可以通过四个角来判断;
如果定义状态为该云目前的坐标,那么,当四个角中其中有不符题意的状态,难以表示;
如果该状态为坐标以及四个角的情况,那么,对于相同状态下,不同天数所处的情况也不同;
综上,定义:状态(time,(x,y),(d1,d2,d3,d4));
因此,对于这样一个状态,是满足唯一性,也就是说,可以保证该状态可以准确描述状态的情况;
连续七天,因此为了保险起见,我们使用八进制状态压缩(d1,d2,d3,d4),即d1 + d2 * 8 + d3 * 64 + d4 * 512;
其余,就注意细节即可;
代码如下:
#include
#include
#include
#include
#include
#include
