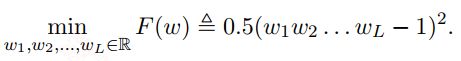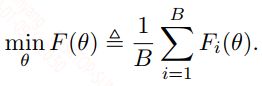1,Introduction
当你想训练好一个神经网络时,你需要做好三件事情:一个合适的网络结构,一个合适的训练算法,一个合适的训练技巧:
合适的网络结构:包括网络结构和激活函数,你可以选择更深的卷积网络,然后引入残差连接。可以选择relu做为激活函数,也可以选择tanh,swish等。
合适的训练算法:通常采用SGD,也可以引入动量和自适应学习速率,也许可以取得更好的效果。
合适的训练技巧:合理的初始化,对于较深的网络引入残差连接,归一化等操作。
作者将上述设计的作用用一个图来表示:
1.1 Big picture: decomposition of theory
一般的监督式机器学习可以归结为Representation,optimization 和 generalization 。
Representation:找到一个能表征目标函数的函数,可以是一个神经网络。
Optimization:寻找最优的参数来最小化损失函数。
Generalization:将训练好的模型用来预测测试集,测试集得到的误差称为测试误差,而测试误差又可以分解为表征误差,优化误差和泛化误差。
一般来说上面三个问题都是单独分开研究的。Optimization是一个复杂的问题,想研究清楚,还需要进一步分解,可以分解为三个方面:能收敛到一个平衡点,收敛的速度足够快,收敛的平衡点是全局最优点。根据这三个方面也就衍生除了一系列的问题:
按照上面的可以归纳为:收敛问题,包括梯度弥散,梯度爆炸等;收敛速度问题;全局最优问题,包括局部最小值,陷入平坦地区,鞍点等。
上面的划分并不是完全准确的,因为这三类问题的边界是比较模糊的,下面会就这三个方面去阐述。
2,Problem Formulation
给定一个数据集${x_i, y_i}$,如下:
我们需要一个映射关系:
上面式子中的$\phi$是激活函数,通常无法直接映射到$y_i$,而是映射到${\hat{y}}_i$,但我们希望两者之间靠的很近,因此:
这就是机器学习定义和优化的基本流程。
3,Gradient Descent: Implementation and Basic Analysis
最常用的优化算法是梯度下降和它的变体,最简单的梯度下降如下:
${\eta} _ t$是学习速率(学习步长),$\nabla F({\theta} _ t)$是梯度值,梯度值通常通过BP(反向传播)算法来求得。而且理论上说在迭代时给定一定的约束下(小的学习速率),梯度下降是会收敛的。
4,Neural-net Specific Tricks
现在训练一个大的神经网络是相对容易的,本章主要探讨神经网络训练中的一些主要技巧。
4.1 Possible Slow Convergence Due to Explosion/Vanishing
训练神经最困难的问题可能是梯度消失和梯度爆炸。常用的梯度下降可以看作是一种反馈校正机制,将网络输出层的误差反向传播到前面的层,调整前面层的权重来减小误差。在这个传递的过程中,梯度可能在每一层被放大或缩小,从而引起梯度爆炸和梯度消失。举一个一维损失函数的例子:
对$w_i$的梯度可以表示为:
上面式子中的$e$是误差,当所有的$w_j = 2$,梯度值会爆炸,当所有的$w_j = 0.5$,梯度会消失。
再看一个例子:
其曲线图如下:
在定义域$[-1 + c, 1 - c]$之间是一块平坦区域,在这里的梯度几乎接近于零,当神经网络训练时进入到这块区域,就会发生梯度消失,而模型需要很漫长的时间才可能达到最小值点$x=1$。而在两侧的梯度又很大,会引起梯度爆炸,不过梯度爆炸已经不是什么问题,梯度截断能很好的解决这个问题。对于这个问题当你初始化$w$的值在1的附近时,你很容易抵达最小值点,但是当你初始化在其他值,比如$w=-1$,此时你需要迭代很久才能到达最小值。另外在神经网络中像极小值点,鞍点,陷入这些点的概率是非常非常低的,尤其是高维空间下,反倒是这类平坦区域才是你通常容易遇到的地方。
作者在这里讨论的梯度消失和梯度爆炸问题都只限于前向网络和卷积网络,不涉及到RNN,因为本质上来看RNN的梯度消失和前向网络的梯度消失原理并不一样,而且难度也更大。从上面也看到一个好的初始化是可以有效的解决这个问题,那么什么是好的初始化?
4.2 Careful Initialization
梯度爆炸和梯度消失区域是确实存在的,而且会占据很大一部分区域,因此一个好的初始化是有可能避开这些区域的。
a) Naive Initialization
我们可以将初始化值全部置为0或者个别非0,其余全为0的稀疏值,又或者是随机无规律的初始值,这种初始化方法通常效果较差,大多数时候都不work。
b) LeCun initialization
c) Xavier initialization
d) Kaiming initialization
上面三种初始化方法可以见神经网络中的权值初始化方法,我做了一些实验来描述三者的特性。
其余略!
4.3 Normalization Methods
归一化可以看作是初始化的扩展,只不过归一化不是作用在初始点,而是作用在后续迭代阶段参数的分布。而归一化最常见的就是batch normalization。除此之外还有layer normalization,instance normalization等等。通常对训练数据我们也会做归一化。
a) Preparation: data normalization
对训练数据的归一化是非常重要的,吴恩达在他的机器学习课程中就讲过这个问题,如果两个特征的值差得非常大的情况下,模型收敛是非常慢的,而归一化可以加快模型收敛的速度。从理论上来讲数据归一化可以减小海森矩阵的条件数,加快梯度下降的收敛速度。
b) Motivation of BatchNorm: layerwise normalization.
说起BN层,基本上都知道是什么,BN层可以看作和卷积层,池化层等类似的神经网络中的一层。上面说到对训练数据归一化是可以加快收敛的,在神经网络中每一层网络都会接受上一层的输入,而上一层的输入大多数时候都会发生分布偏移的现象,也就是在深层隐层中的输入可能已经不服从(0, 1)的正态分布了。BN层在这里的作用就是将每一层的输出都从新归一化然后输入到下一层,这种方式可以加快网络的收敛速度,除此之外还可以缓解梯度消失的问题。
c) Other normalization methods
BN虽说好用,但也有他的一些问题,以及应用的局限性,BN是作用在一个batch上的,当batch size较小时容易引入噪声,在求均值和方差时会不准确,另外就是在预测时无法计算均值和方差,只能使用训练时保存的滑动平均值。除了上面的缺点,BN因为是在batch size个样本,单个channel上计算的,对于NLP中的应用就受限了,因为每个句子的长度不一样,而对于长度较长的句子,后面的词向量的归一化就只有几个甚至一个词可以使用。由于这些原因也就衍生出了其他的normalization的方法,总体来说可以分为两种,一种是和BN一样的对输入归一化,例如layer normalization,LN也是在NLP中用的最多的归一化方法。另一种就是直接对权重归一化,如weight normalization。但感觉这种方法用的很少,应该效果不太好。
4.4 Changing Neural Architecture
加深网络的深度可以提升网络的性能,这一点已经被太多例子给证明,而且从网络的深度和宽度来看,之前周志华老师一次报告中就提到过加深网络比加宽网络的收益更高。这一点在CNN中已经被证明,但在RNN中并没有这样的情况,Transformer应该有这样的迹象。
像ResNet,Highway Network等的设计都是为了加深网络,而ResNet也实现了很深的网络层,广泛在CNN,以及Transformer等网络中使用。另外最近比较火的NAS也可以去做这个事情,不一定是寻求更深的网络结构,但是可以寻求更合理的网络结构。而从resnet来看,resnet学习到的这种恒等映射行为至少能保证更深的网络不会比更浅的网络差,此外在反向传播过程中因为这样一个非乘积的操作存在,也可以一定程度缓解梯度消失,梯度爆炸的问题,而梯度消失和梯度爆炸是深层网络中最容易出现的问题。
4.5 Training Ultra-Deep Neural-nets
也有人在训练一些超深的网络(比如大于1000层),此时你需要一个很好的初始化参数,需要用到resnet和BN层。除此之外,你可能还需要从数据预处理,优化算法,激活函数,正则化等方面去下功夫。
5,General Algorithms for Training Neural Networks
一个好的优化算法需要保证两点:一是收敛速度够快,二是能收敛到更优的点,也就是模型在我们给定的性能指标上表现更好。这两点之间并没有太多连续,也就是说收敛更快并不一定能导致收敛更好。接下来就讨论下相关优化算法。
5.1 SGD and learning-rate schedules
给定一个需要优化的问题:
上面的式子中$F(\theta)$就是一个batch上计算得到的损失函数,在第$t$次迭代更新中,利用SGD优化算法,可以将式子写成:
一般来说我们都是在batch上做梯度下降,batch是你的训练样本中的一小部分(通常取32, 64, 128),尽量保持每次取得batch不一样。
Reasons for SGD: memory constraint and faster convergence
为什么使用SGD而不是GD,从内存上来看,单机很难讲整个数据集一起处理,只能处理batch size个数据集。而且SGD从收敛速度上也比GD更快。
Vanilla learning rate schedules
学习速率通常是一个较小的值,用来控制每次梯度下降的量,有时候会用一个常量,但由时候又会根据迭代的次数去减小学习速率,因为在靠近收敛阶段,我们希望模型能降低下降的速度,防止跳过了最小值点。
Learning rate warmup
warmup这个东西是在现在这些较深的网络,数据量较大的时候,而又使用较小的batch size的时候有效的。为什么这么说呢?首先来看下warmup是怎么工作的,公式如下:
$lr_{warmup} = lr * (global step / warmup step)$
在训练步数小于$warmup step$时,采用上面的学习速率,超过这个步数就采用$lr$。从这里可以看到一开始的学习速率是一个非常小的值,假设$warmup step = 1000$,一开始的学习速率就是你设置的0.001倍。这样的做法是因为一开始初始化的参数离真实分布较远,而采用mini-batch的方式训练,每个batch中样本的方差较大,如果一开始的学习速率比较大,参数的分布容易跑偏,而且一旦跑偏了,在现在这种参数比较多的深度神经网络中就很难再调回来。因此才需要在一开始给一个很小的学习速率,让模型慢慢调整参数,当参数调整的类似真实分布时,再给大一点的学习速率加快模型的收敛。从上面分析中也可以看到,当batch size很大时,或者模型很小时,就不太需要warmup。(注意这个batch size是相对训练集大小而言的,没有绝对的大或小)。
Cyclical learning rate
这种学习速率用的比较少,通常要么固定学习速率,要么让学习速率衰减,但这种是让学习速率在一个范围内循环,也就是说学习速率会下降然后突然上升,再接着下降。这样的话就可以在模型陷入鞍点等地方能更容易地跳出来。
5.2 Theoretical analysis of SGD
分析SGD的理论
Constant v.s. diminishing learning rate
这是一个常量学习速率和衰减学习速率的争论问题,常量学习速率可能在最后收敛阶段收敛不到最小值,而是在震荡。但衰减学习可能会导致收敛速度很慢。
New analysis for constant learning rate: realizable case
针对上面的问题,也就是常量学习速率能不能收敛到最小值。如果是服从"zero global minimal value" (也即是全局最小值为0)这样的强假设,那么常量学习速率就可以收敛(懵逼中),而无所不能的神经网络是符合这样的假设的(再次懵逼中),不管怎么说,常量学习速率用的是越来越小,而训练神经网络也没指望能收敛最全局最优点,能接近就不错了。
Acceleration over GD
举一个例子证明了SGD的收敛速度是要快于GD的。这个东西其实可以直观点理解,GD要计算全样本,SGD只要计算部分样本,但迭代收敛的步数的差距应该是要小于样本计算量差的,虽然batch样本计算的梯度可能较GD有偏差,但总体方向是一样的,多一些迭代就可以同样收敛了,而且这种偏差有时候也可以模型跳出局部最优。
5.3 Momentum and accelerated SGD
动量法是在SGD中引入动量,其实就是之前的滑动平均梯度值,表达式如下:
引入动量的作用其实是为了减小梯度方差,我们认为历史梯度的滑动均值是朝着最优方向的,而当前的batch可能方差较大,带偏了梯度下降的方向,所以这个目的主要是为了纠正方向,以此来加速收敛,但具体能不能起到加速的效果,并不一定在每个网络都有效。
5.4 Adaptive gradient methods: AdaGrad, RMSProp, Adam and more
自适应学习速率是现在优化算法中用的很多的一种技巧,包括上面的动量法,如Adagrad,其表达式如下:
上面式子中$v_t$就起到控制学习速率$a_t$的作用,从这里看会随着迭代次数的增加,$v_t$会急剧增大,学习速率会迅速衰减,因此后续很多带自适应的优化算法,如RMSProp,ADAM等都对$v_t$做了修改,以更好的适应学习速率的变化。
自适应学习速率有效的原因是因为在实际训练过程中有的参数被更新的次数较多,而有的参数被更新的次数较少,如果用同一学习速率,可能有的参数已经到最优了,而有的还差很远,这就是自适应学习速率有效的原因。目前使用的最多的优化算法就是ADAM了,ADAM基本上都能work,也能快速的收敛,但从最终的性能来看,是不如精心调试的SGD或者SGD+动量的方法好。另外对于凸函数的优化,ADAM可能不收敛,就如上面说的对于凸函数问题,常量学习速率的SGD容易发散,而衰减的学习速率的SGD会收敛,在这里ADAM的学习速率并不会衰减,Adagrad会一直衰减。所以ADAM在凸问题可能发散,但神经网络基本是非凸的,所以大胆使用,也有解决这个问题的,例如AMSGrad,其$v_t$的计算如下:
5.5 Large-scale distributed computation
在加速神经网络训练时,还可以采用分布式平行计算的方法。使用多台机器来训练,其加速的比例取决于三点:通信时间,同步时间和收敛速度,收敛速度主要受多台机器上数据的影响,如果数据都相同,则无法加速。
分布式计算的策略基本就两种:同步计算和异步计算。同步计算一般是多台机器同时计算少量样本的梯度,然后合并到主机器上求平均来更新模型,讲更新后的模型参数同步到其他机器,这种情况如木桶效应,会受到计算最慢的机器的影响。而异步是每台机器自己更新自己的,但是可能会出现这台机器计算的梯度用的参数是好几次之前的,会降低收敛速度。
6,Global Optimization of Neural Networks (GON)
神经网络一般是一个非凸优化问题,而由于局部最优的存在,导致非凸优化非常困难。而本章就在讨论怎么解决最优问题
6.1 Related areas
意义不大,跳过。
6.2 Empirical exploration of landscape
有很多工作证明,在实际的神经网络优化过程中,并没有发现局部最优,或者说并不容易陷入局部最优,更多是陷入平坦地区,比如高原。像鞍点这种碰到的概率比局部最优大,但也是非常容易逃离的,反倒是这种平坦地区,一旦陷入就很难出来,因为这里的梯度值太小。
6.2.1 Mode connectivity
没看懂,跳过。
6.2.2 Model compression and lottery ticket hypothesis
这里其实和模型压缩有关,对于一个好的网络不应该只是性能优化,网络也应该更简单些,但实际上我们需要训练一个很大的网络才能取得很好的效果,基本上都是过参数的,通过网络剪枝就能证明这一点,一个大的网络剪掉一部分参数,性能基本不变,这也说明大网络的参数都是过量的,但是从这个剪枝后的小网络必须继承大网络的参数才能保证好的性能,而从零开始训练这个小网络就没有这样的效果。
在彩票假设中发现这样一个问题,训练好一个大网络,然后从中找到一个最优的小网络结构,接着用大网络的原始初始化值来初始化这个小网络,然后从零训练小网络也可以达到大网络的效果,但是对小网络随意初始化值就达不到这样的效果。用彩票理论来讲就是,你想买到一个中奖的彩票,你需要买很多彩票,而这个很多彩票就是大网络的参数,但当你中奖了,你就知道中奖的彩票是什么样子,就可以一开始就按照这种标准选择彩票。但为什么随机初始化又不行呢?这个我认为你换了一种初始化就类似于换了一种类型的彩票,你有不知道中奖的是哪种。因此可以认为对于大的神经网络,如果初始化值不一样,重要的权重值也会发生变化。
彩票假设又是怎么做的呢?先训练一个大网络,然后构建一个mask矩阵,mask矩阵根据大网络参数值的大小来构建的,参数大于某个值,mask矩阵中的值置为1,否则置为0,用这个mask矩阵去选择小网络结构。然后用大网络的原始初始化参数来初始化这个小网络,从新训练这个小网络即可。
其实从假设空间来理解也可以,一个大的假设空间更能保证有一个假设离真实假设很近,而大的模型正好有大的假设空间,但实际上我们只要这个大的假设空间中靠近真实假设的一个小空间即可,在这个小空间中搜索就能找到模型最优值。但是这个小空间我们一开始很难确定在哪,所以只能拿大空间来增大运气。
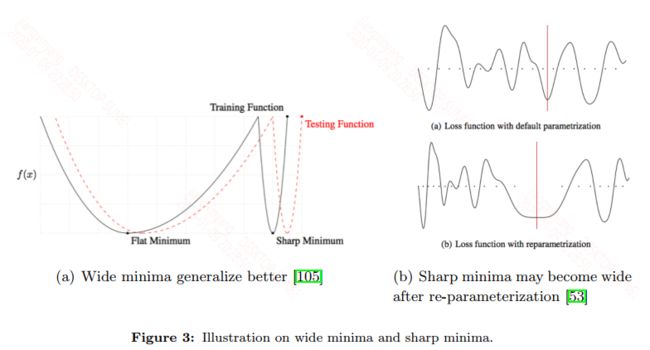
6.2.3 Generalization and landscape
讨论宽窄的极小值区域对泛化性能的影响,作者图示展示了多种形状的极小值:
大多数认为宽区域的极小值的泛化性是要优于窄区域的极小值,而像SGD这种算法是容易进入到宽区域的极小值。
其余略!
参考文献:
Optimization for deep learning: theory and algorithms