题目
给定一个单词列表,我们将这个列表编码成一个索引字符串 S 与一个索引列表 A。
例如,如果这个列表是 ["time", "me", "bell"],我们就可以将其表示为 S = "time#bell#" 和 indexes = [0, 2, 5]。
对于每一个索引,我们可以通过从字符串 S 中索引的位置开始读取字符串,直到 "#" 结束,来恢复我们之前的单词列表。
那么成功对给定单词列表进行编码的最小字符串长度是多少呢?
示例:
输入: words = ["time", "me", "bell"]
输出: 10
说明: S = "time#bell#" , indexes = [0, 2, 5] 。
提示:
1 <= words.length <= 2000
1 <= words[i].length <= 7
每个单词都是小写字母 。
思路
从第二个单词开始,与前一个循环倒着比较。记录相同的计算。
笨比解法,最多通过25/30个样例。基本不可能改好了。心累

还是看看官方代码吧。
代码
class Solution:
def minimumLengthEncoding(self, words: List[str]) -> int:
good = set(words)
for word in words:
for k in range(1, len(word)):
good.discard(word[k:])
return sum(len(word) + 1 for word in good)
链接:https://leetcode-cn.com/problems/short-encoding-of-words/solution/dan-ci-de-ya-suo-bian-ma-by-leetcode-solution/
来源:力扣(LeetCode)
set()方法
set() 函数创建一个无序不重复元素集,可进行关系测试,删除重复数据,还可以计算交集、差集、并集等。
例:
a='handsome'
print(set(a))
结果:
{'o', 'n', 'h', 's', 'e', 'm', 'a', 'd'}
这个元素集,可以使用,update,remove,add等方法
a='handsome'
b=set(a)
print(b)
b.add('me')
b.update('are')
print(b)
b.update('are')
print(b)
b.remove('are')
print(b)
结果:
{'o', 's', 'e', 'm', 'n', 'a', 'h', 'd'}
{'o', 's', 'e', 'm', 'n', 'r', 'me', 'a', 'h', 'd'}
{'o', 's', 'e', 'm', 'n', 'r', 'me', 'a', 'h', 'd'}
set() discard与remove
discard() 方法用于移除指定的集合元素。
该方法不同于 remove() 方法,因为 remove() 方法在移除一个不存在的元素时会发生错误,而 discard() 方法不会。
字典树
思路
如方法一所说,目标就是保留所有不是其他单词后缀的单词。
算法
去找到是否不同的单词具有相同的后缀,我们可以将其反序之后插入字典树中。例如,我们有 "time" 和 "me",可以将 "emit" 和 "em" 插入字典树中。
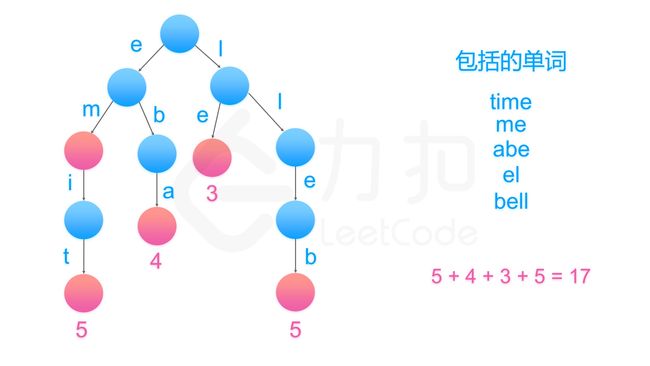
然后,字典树的叶子节点(没有孩子的节点)就代表没有后缀的单词,统计叶子节点代表的单词长度加一的和即为我们要的答案。
链接:https://leetcode-cn.com/problems/short-encoding-of-words/solution/dan-ci-de-ya-suo-bian-ma-by-leetcode-solution/
来源:力扣(LeetCode)
代码
class Solution:
def minimumLengthEncoding(self, words: List[str]) -> int:
words = list(set(words)) #remove duplicates
#Trie is a nested dictionary with nodes created
# when fetched entries are missing
Trie = lambda: collections.defaultdict(Trie)
trie = Trie()
#reduce(..., S, trie) is trie[S[0]][S[1]][S[2]][...][S[S.length - 1]]
nodes = [reduce(dict.__getitem__, word[::-1], trie)
for word in words]
#Add word to the answer if it's node has no neighbors
return sum(len(word) + 1
for i, word in enumerate(words)
if len(nodes[i]) == 0)
