问题描述
一个点(源点)到其余各个顶点的最短路径,也叫做“单源最短路径”。
例如求下图中的1号顶点到2、3、4、5、6号顶点的最短路径。
问题解释
-
使用二维数组e来存储顶点之间边的关系
-
一维数组dis来存储1号顶点到其余各个顶点的初始路程
dis数组中的值称为最短路的“估计值”。
1到2号通过dis可知为最短。再看2号有什么出边。
2>3 or 2>4 , 2到3能否让1到3的路程变短?比较dis[3]和dis[2]+e[2][3]的大小
dis[3] = 1到3
dis[2]+e[2][3] 1到2 再通过2-3到3号
dis[2] = 1到2
e[2][3]= 2->3dis[3]=12,
dis[2]+e[2][3]=1+9=10,
dis[3]>dis[2]+e[2][3],
更新
dis[3]为10
-专业术语叫做“松弛”
1-3为dis[3],通过2->3这条边松弛成功。
-同理
通过2->4(e[2][4])
将dis[4]的值从∞松弛为4
dis[4] = ∞,dis[2] + e[2][4] = 1 + 3 = 4
dis[4] > dis[2] + e[2][4]
so更新dis[4]为4
Dijkstra算法的主要思想:通过“边”来松弛1号顶点到其余各个顶点的路程。
因此得出可以通过松弛的方法计算dis数组!
-
最终结果
-总结
基本思想:找到最近顶点,进行扩展,得出最近顶点的最短路径。
解题思路
- 顶点可分为两类
已知最短路程的顶点集合P
未知最短路径的顶点集合Q
已知最短路径的顶点集合P中只有源点一个顶点 1
book[ i ]数组记录那些在P中
book[ i ]=1 表示 i在P中
book[ i ]=0表示i在Q中
- 源点
源点s到自己的最短路径为0
即dis=0
源点有能直接到达的顶点i
dis[ i ]设为e[s][ i ]
- 集合Q的所有顶点中选择一个离源点s最近的顶点u(即dis[u]最小)
加入到集合P
考察所有以点u为起点的边,对每一条边进行松弛操作。
可将u-v添加到s-v的路径
dis[u]+e[u][v]
比目前已知的dis[v]的值要小,则替代dis[v]
-重复第3步,如果集合Q为空,算法结束
解法
-代码
#include
int main()
{
int e[10][10],dis[10],book[10],i,j,n,m,t1,t2,t3,u,v,min;
int inf=99999999; //用inf(infinity的缩写)存储一个我们认为的正无穷值
//读入n和m,n表示顶点个数,m表示边的条数
scanf("%d %d",&n,&m);
//初始化
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j) e[i][j]=0;
else e[i][j]=inf;
//读入边
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&t1,&t2,&t3);
e[t1][t2]=t3;
}
//初始化dis数组,这里是1号顶点到其余各个顶点的初始路程
for(i=1;i<=n;i++)
dis[i]=e[1][i];
//book数组初始化
for(i=1;i<=n;i++)
book[i]=0;
book[1]=1;
//Dijkstra算法核心语句
for(i=1;i<=n-1;i++)
{
//找到离1号顶点最近的顶点
min=inf;
for(j=1;j<=n;j++)
{
if(book[j]==0 && dis[j]dis[u]+e[u][v])
dis[v]=dis[u]+e[u][v];
}
}
}
//输出最终的结果
for(i=1;i<=n;i++)
printf("%d ",dis[i]);
getchar();
getchar();
return 0;
}
时间复杂度
O(N2N)
每次找到离1号顶点最近的顶点的时间复杂度是O(N)
可以用“堆”来优化,时间复杂度降低到O(logN)。
对于边数M少于N2的稀疏图来说
可以用邻接表来代替t 邻接矩阵,复杂度优化到O(MlogN)
优化
https://blog.csdn.net/ahalei/article/details/23356781
另外一种存储图的方法:邻接表,这样空间和时间复杂度就都是M。对于稀疏图来说,M要远远小于N2。先上数据,如下。
第一行两个整数n m。
n表示顶点个数(顶点编号为1~n),
m表示边的条数。
接下来m行表示,
每行有3个数x y z,表示顶点x到顶点y的边的权值为z。下图就是一种使用链表来实现邻接表的方法。
每个顶点都建立了一个单链表
可以通过遍历
得出每个的点边
- 解法
为每一条边编号!1-m,1,4,9
u、v和w三个数组用来记录每条边的具体信息,即u[i]、v[i]和w[i]表示第i条边是从第u[i]号顶点到v[i]号顶点,且权值为w[i]。
first数组来存储每个顶点其中一条边的编号
假如1号顶点有边1 4 9, 将first[1]设为1,顶点i没有以1 4 9则设为-1
下标为一,第一条边 14 9,
u[i]为起始点的第一条边,就将next[i]的值设为-1
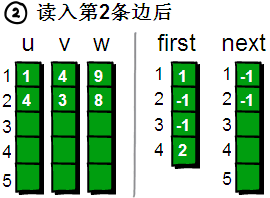
下标2 读入4 3 8
4号顶点为起始点的第一条边,所以将next[2]的值设为-1。
读入第3条边(1 2 5)
起点为1,但是1条已经是1开头了,所以讲next设为1
读入第四条边246 2号顶点为起始点的第一条边,所以将next[4]的值设为-1。
读入第5条边(1 3 7)
这条边的编号为5,起始顶点又是1号顶点。此时需要将first[1]的值设为5,并将next[5]的值改为3。
读入第5条边(1 3 7),将
将first[1]的值设为5,并将next[5]的值改为3。
遍历1号顶点
int n,m,i;
//u、v和w的数组大小要根据实际情况来设置,要比m的最大值要大1
int u[6],v[6],w[6];
//first和next的数组大小要根据实际情况来设置,要比n的最大值要大1
int first[5],next[5];
scanf("%d %d",&n,&m);
/初始化first数组下标1~n的值为-1,表示1~n顶点暂时都没有边
for(i=1;i<=n;i++)
first[i]=-1;
for(i=1;i<=m;i++)
{
scanf("%d %d %d",&u[i],&v[i],&w[i]);//读入每一条边
next[i] = first[u[i]];
first[u[i]]= i;
遍历1号顶点所有边的代码如下。
k = first[1]; //
while (k!-1_
{
printf("%d %d %d \n", u[k], v[k], w[k]);
k = next[k];
遍历每个顶点的所有边的代码如下。
for(i=1;i<=n;i++)
{
k=first[i];
while(k!=-1)
{
printf("%d %d %d\n",u[k],v[k],w[k]);
k=next[k];
}
}