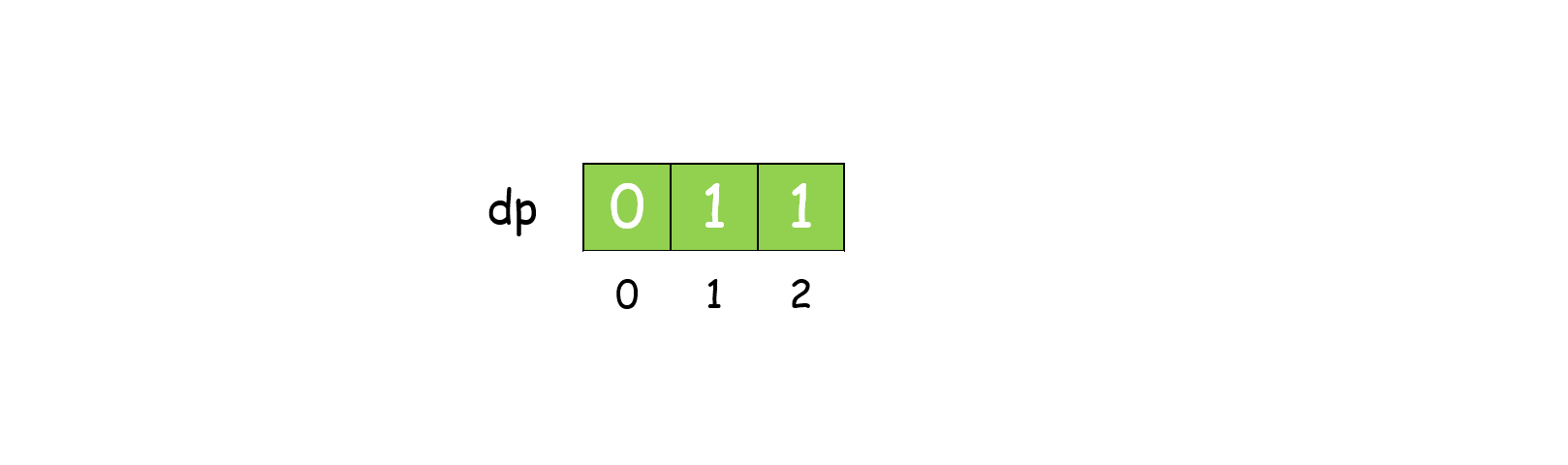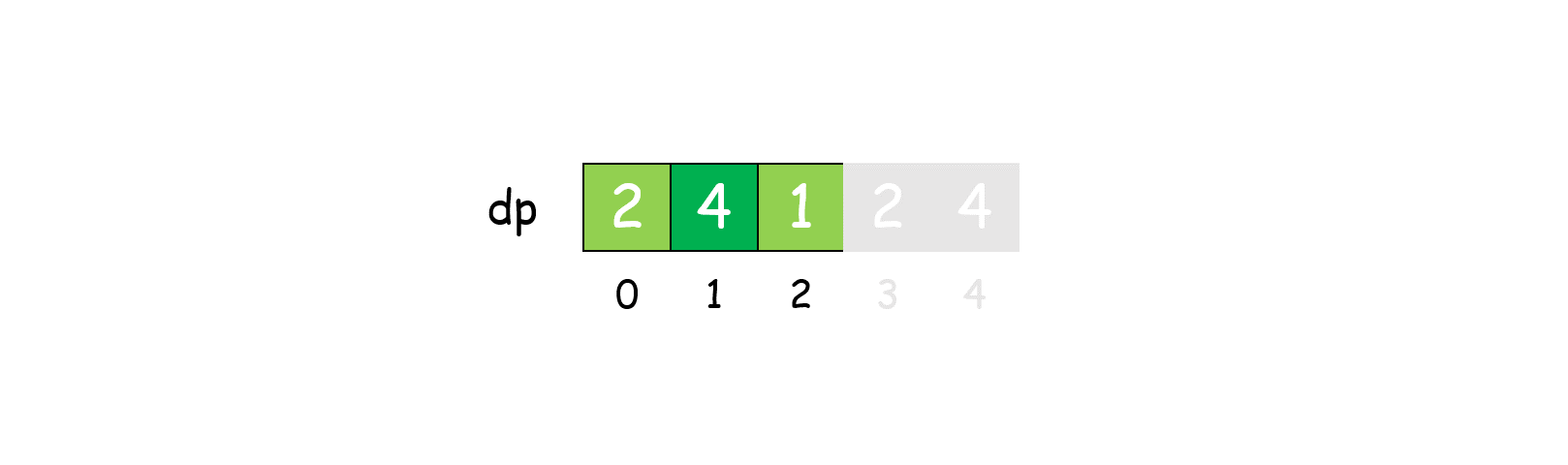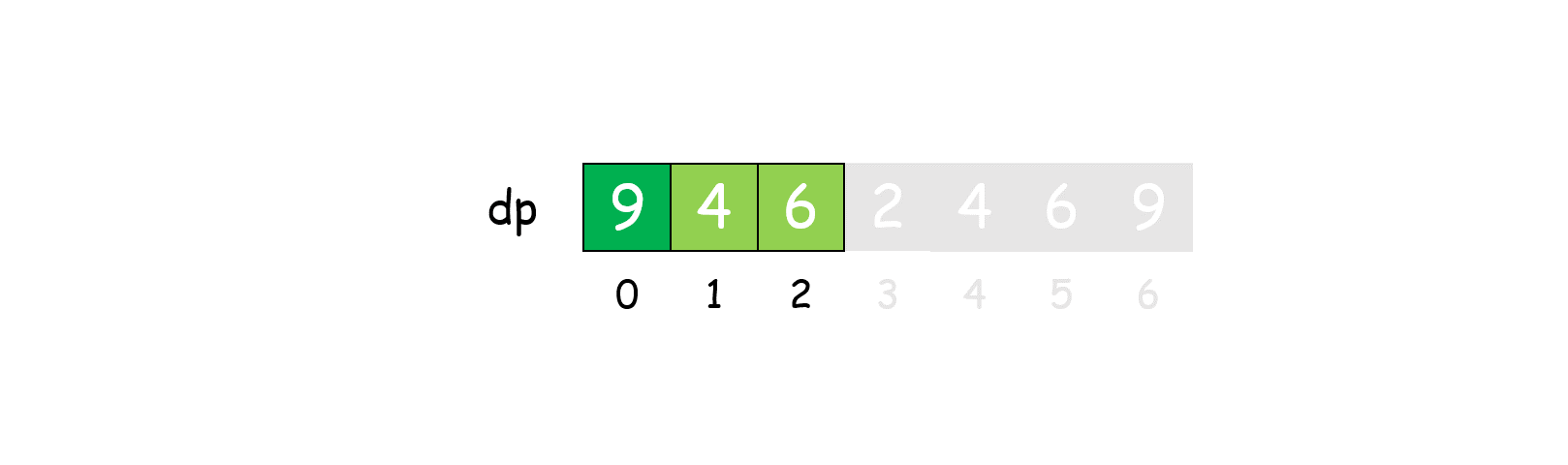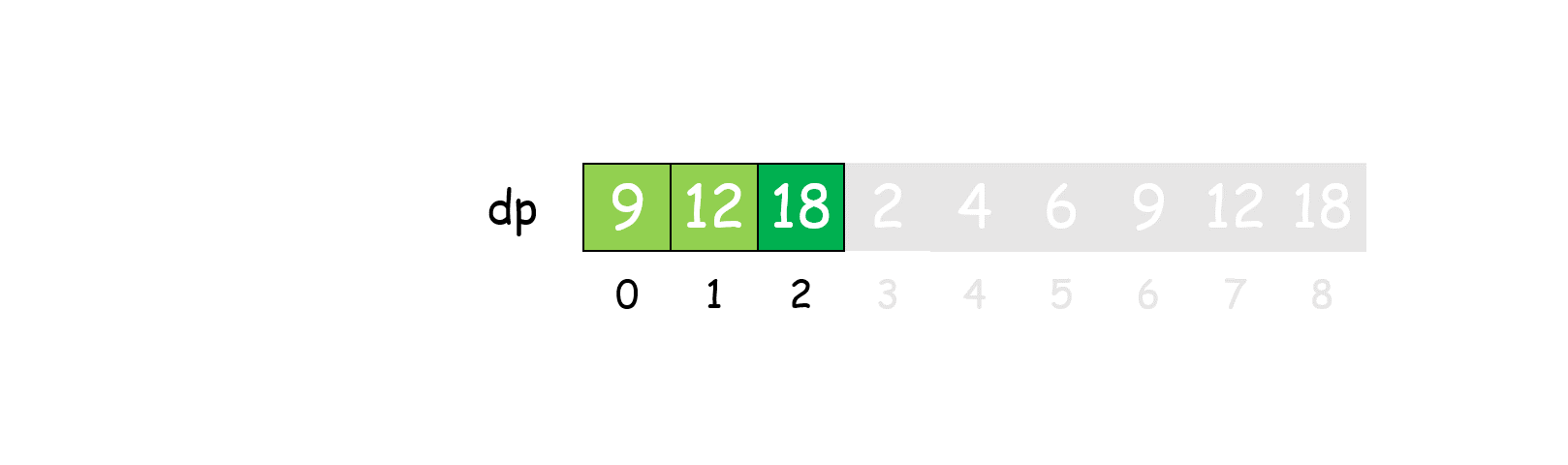转自:https://leetcode-cn.com/problems/jian-sheng-zi-lcof/solution/xiang-jie-bao-li-di-gui-ji-yi-hua-ji-zhu-dong-tai-/
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m] 。请问 k[0]*k[1]*...*k[m] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
示例 1:
输入: 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:
输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
提示:
2 <= n <= 58
题解思路:
方法一:暴力递归
我们往往会在头脑中形成一种很直观的暴力解法,就是列举出所有的情况,找到乘积最大的那个解。
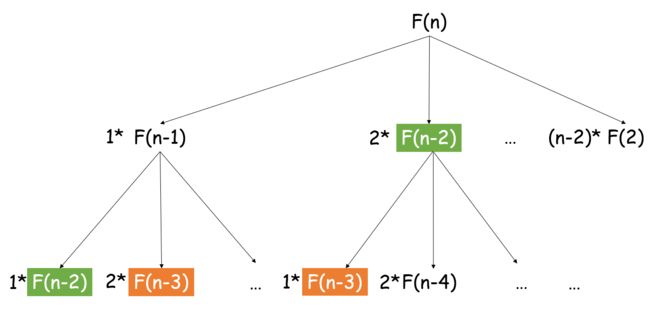
设 F(n) 为长度为 n 的绳子可以得到的最大乘积,对于每一个 F(n),可以得到如下分解:
从上图看出我们可以把求解 F(n)的问题分解成求解 F(n−1)的问题,以此类推,直到求解到 F(2) 时,1F(2)=1,递推回去,问题就得到了解决。这用到的就是分治的思想。
分治思想的解决方法往往是递归,注意到我们每次将一段绳子剪成两段时,剩下的部分可以继续剪,也可以不剪, 因此我们得到了递归函数 F(n)=max(i×(n−i),i×F(n−i)),i=1,2,...,n−22F(n)=max(i×(n−i),i×F(n−i)),i=1,2,...,n−2。
代码(超时)
- python
class Solution:
def cuttingRope(self, n: int) -> int:
if n == 2:
return 1
res = -1
for i in range(1, n):
res = max(res, max(i * self.cuttingRope(n - i),i * (n - i)))
return res
复杂度分析
- 时间复杂度:O(N^2),对于每一个
i调用一次递归,递归的时间复杂度为 O(N),故时间复杂度为 O(N^2)。 - 空间复杂度:O(N^2)
方法二:记忆化技术(自顶向下)
上述暴力解法会超时,但是很多进阶解法往往是暴力解法的优化。注意到上述代码中超时的原因主要是因为重复计算了 F(n),为了避免重复计算可以使用 记忆化(memoization) 技术(维基百科)。
记忆化技术的代码中经常需要建立函数 memoize 辅助实现。我们使用数组 f 来保存长度为 i时的最大长度 f[i],最后返回 f[n]即可。
代码
- python
class Solution:
def cuttingRope(self, n: int) -> int:
# 使用辅助函数
def memoize(n):
if n == 2: return 1
if f[n] != 0: # 如果f[n]已经计算过,直接返回避免重复计算
return f[n]
res = -1
for i in range(1, n):
res = max(res, max(i * (n - i),i * memoize(n - i)))
f[n] = res
return res
f = [0 for _ in range(n + 1)]
return memoize(n)
复杂度分析
- 时间复杂度:O(N^2),原因同上,时间复杂度仍然为 O(N^2),只是采用记忆化减少部分计算时间。
- 空间复杂度:O(N)。使用了数组
f。
(记忆化技术 相关题目:70.爬楼梯,509.斐波那契数)
记忆化搜索也叫“备忘录法”,它从类似上边树形图结构中的 F(n) 出发,逐步递归到已知值 F(2),可以理解成为自顶向上的解决办法。
方法三:动态规划(自底向上)
同样地,我们也可以使用动态规划,从已知值 F(2)F(2)F(2) 逐步迭代到目标值 F(n)F(n)F(n),它是一种自底向上的方法。
算法
建立一维动态数组 dp:
- 边界条件:
dp[1] = dp[2] = 1,表示长度为2的绳子最大乘积为1; - 状态转移方程:
dp[i] = max(dp[i], max((i - j) * j, j * dp[i - j])),可以这样理解:
代码
- python
class Solution:
def cuttingRope(self, n: int) -> int:
dp = [0 for _ in range(n + 1)] # dp[0] dp[1]其实没用
dp[2] = 1 # 初始化
res = -1
for i in range(3, n + 1):
for j in range(i):
dp[i] = max(dp[i], max((i - j) * j, j * dp[i - j]))
return dp[n]
复杂度分析
- 时间复杂度:O(N^2)。
- 空间复杂度:O(N)。
方法四:动态规划优化解法
我们发现任何大于 333 的数都可以拆分为数字 1,2,31,2,31,2,3 的和,且它们对 333 的余数总是 0,1,20,1,20,1,2,因此我们可以仅用 dp[0],dp[1],dp[2] 表示所有大于 333 的值,这样空间复杂度可降到 O(1)O(1)O(1)。
这样重复使用 dp 数组,只须一趟遍历即可完成,可使时间复杂度降到 O(N)。
代码
- python
class Solution:
def cuttingRope(self, n):
dp = [0, 1, 1]
for i in range(3, n + 1):
dp[i % 3] = max(max(dp[(i - 1) % 3], i - 1),
2 * max(dp[(i - 2) % 3], i - 2),
3 * max(dp[(i - 3) % 3], i - 3))
return dp[n % 3]
复杂度分析
- 时间复杂度:O(N)。
- 空间复杂度:O(1)。使用了有限长的数组。
方法五:找规律
在面试时尽量按照常规思路去解,但是大神 @jyd 提出了一种非常巧妙的解法,可将时间复杂度降到 O(1),值得我们去学习,他在 题解 中进行了详细的说明,这里只进行简单的总结。
贪心法则:尽可能分解出多的 333,333 的个数为 a,得到余数 b 可能为 0,1,20,1,20,1,2:
b = 0,返回 3a3^a3a;b = 1,我们将末尾的 3+13+13+1 分解成 2×22\times 22×2,因此返回 3a−1×43^{a-1}\times 43a−1×4;b = 2,返回 3a×23^a\times 23a×2;
代码
- python
- cpp
class Solution:
def cuttingRope(self, n: int) -> int:
if n < 4: return n - 1
a, b = n // 3, n % 3
if b == 0:
return pow(3, a)
elif b == 1:
return pow(3, a - 1) * 4
else:
return pow(3, a) * 2
class Solution {
public:
int cuttingRope(int n) {
if (n < 4)return n - 1;
int a = n / 3, b = n % 3;
if (b == 0)return a = pow(3, a);
if (b == 1)return a = pow(3, a-1) * 4;
if (b == 2)return a = pow(3, a) * 2;
return a;
}
};
复杂度分析
- 时间复杂度:O(1)。
- 空间复杂度:O(1)。
链接:https://leetcode-cn.com/problems/jian-sheng-zi-lcof