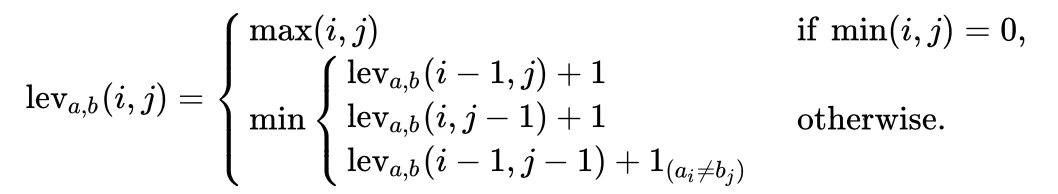首先先学习一个经典的算法吧,就是和本题一模一样的“编辑距离算法”。编辑距离,Minimum Edit Distance,简称MED,是俄罗斯科学家 Vladimir Levenshtein 在1965年提出,也因此而得名 Levenshtein Distance。
- 定义 指的是 中前 个字符和 中前 个字符之间的距离。为了方便理解,这里的可以看作是的长度。这里的字符串的第一个字符 index 从 1 开始(实际因为在表上运算的时候字符串前需要补 0),因此最后的编辑距离便是 时的距离:
-
当 的时候,对应着字符串 中 前 个字符和 字符串 中 前 个字符,此时的 有一个值为 0 ,表示字符串 a 和 b 中有一个为空串,那么从 a 转换到 b 只需要进行 次单字符编辑操作即可,所以它们之间的编辑距离为 ,即 中的最大者。
- 当 的时候, 为如下三种情况的最小值:
1. 表示 删除
2. 表示 插入
3. 表示 替换 - 为一个指示函数,表示当 的时候取 0 ;当 的时候,其值为 1。
题目:给定两个单词 word1 和 word2,计算出将 word1 转换成 word2 所使用的最少操作数 。你可以对一个单词进行如下三种操作:
1.插入一个字符
2.删除一个字符
3.替换一个字符
分析:根据上面的“编辑距离算法”我们自然而然的就会想到使用动态规划来解决这个题目,
1.定义一个数组二维dp,dp[i][j]表示字符串word1中前i个字符和word2中前j个字符之间的距离,此处的i、j可以看作word1和word2的这两个字符串的长度;
2.根据上面的算法,我们可以得出dp的元素之间的关系式,即:
if min(i,j) ==0, 那么 dp[i][j] = max(i,j);
if min(i,j) != 0,那么
if word1[i] == word2[j],那么dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1])
if word1[i] != word2[j],那么dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+1)
最终,dp[|word1|][|word|2]即为所求的最小值。
public int minDistance(String word1, String word2) { if (Math.min(word1.length(),word2.length())==0) return Math.max(word1.length(),word2.length()); int m = word1.length(); int n = word2.length(); int[][] dp = new int[m+1][n+1]; for (int i = 1; i <= m; i++) { dp[i][0] = i; } for (int j = 1; j <= n; j++) { dp[0][j] = j; } for (int i = 1; i <= m; i++) { for (int j = 1;j <= n;j ++){ if (word1.charAt(i-1) == word2.charAt(j-1)){ dp[i][j] = Math.min(Math.min(dp[i-1][j]+1,dp[i][j-1]+1),dp[i-1][j-1]); }else { dp[i][j] = Math.min(Math.min(dp[i-1][j]+1,dp[i][j-1]+1),dp[i-1][j-1]+1); } } } return dp[m][n]; }
题目来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/edit-distance
编译距离算法参考自:
链接:https://www.jianshu.com/p/a617d20162cf