数据结构导论之第四章树

一、树的基本概念

　　树型结构是一类重要的非线性结构。树型结构是结点之间有分支，并且具有层次关系的结构，它非常类似于自然界中的树。树结构在客观世界中是大量存在的，例如家谱、行政组织机构都可用树形象地表示；树在计算机领域中也有着广泛的应用，例如在编译程序中，用树来表示源程序的语法结构；在数据库系统中，可用树来组织信息；在分析算法的行为时，可用树来描述其执行过程等等。

递归是树的固有特性；

树：是n(n>=0)个结点的有限集T，满足：

• (1)当n=0时，称为空树；
• (2)当n>0时，有且仅有一个特定的称为根的结点；其余的结点可分为m(m>=0)个互不相交的子集T1,T2,T3…Tm，其中每个子集 Ti 又是一棵树，并称其为子树。

●结点：由一个数据元素及若干指向其它结点的分支所组成。
●度：结点的度：所拥有的子树的数目;树的度 ：树中所有结点的度的最大值
●叶子（终端结点）：度为0的结点
●非终端结点：度不为0的结点。
●孩子（子结点）：结点的子树的根称为该结点的孩子。
●双亲（父结点）：一个结点称为该结点所有子树根的双亲
●祖先结点：祖先指根到此结点的一条路径上的所有结点。
●子孙结点：从某结点到叶结点的分支上的所有结点称为该结点的子孙。
●兄弟结点：同一双亲的孩子之间互称兄弟。（父结点相同的结点）
●结点的层次：从根开始算起，根的层次为1,其余结点的层次为其双亲的层次加1。
●堂兄弟：其双亲在同一层的结点。
●树的深度（高度）：一棵树中所有结点层次数的最大值。
●有序树：若树中各结点的子树从左到右是有次序的，不能互换，称为有序树。
●无序树：若树中各结点的子树是无次序的，可以互换，则成为无序树。
●森林：是m（≥0）棵树的集合。

对于任何一棵树：节点数=分支数+1

例如：在一颗度为3的树中，度为3的结点有4个，度为2的结点有2个，度为1的结点有3个，，则度为0的节点有几个

节点数=分支数+1=》4+2+3+n=3*4+2*2+1*3+0*n+1=》n=11

树的基本运算

• ➢ 求根Root(T):求树T的根结点；
• ➢ 求双亲Parent(T,X):求结点X在树T上的双亲；若X是树T的根或X不在T上，则结果为一特殊标志；
• ➢ 求孩子Child(T,X,i):求树T上结点X的第i个孩子结点；若X不在T上或X没有第i个孩子，则结果为一特殊标志；
• ➢ 建树Create(X,T1,…,Tk),k>1:建立一棵以X为根，以T1,…,Tk为第1,…,k棵子树的树；
• ➢ 剪枝Delete(T,X,i):删除树T上结点X的第i棵子树；若T无第i棵子树，则为空操作；
• ➢ 遍历TraverseTree(T):遍历树，即访问树中每个结点，且每个结点仅被访问一次。

 二、二叉树

二叉树在树结构的应用中起着非常重要的作用，因为二叉树有许多 良好的性质和简单的物理表示，而任何树都可以与二叉树相互转换，这 样就解决了树的存储结构及其运算中存在的复杂性

二叉树是n(n>=0)个结点的有限集合，它或为空(n=0)， 或是由一个根及两棵互不相交的左子树和右子树组成，且 中左子树和右子树也均为二叉树。二叉树可以是空集合， 左子树可以为空 、右子树也可以为空。

二叉树的特点：

• ①二叉树可以是空的，称空二叉树；
• ②每个结点最多只能有两个孩子；
• ③子树有左、右之分且次序不能颠倒。

 二叉树结点的子树要区分左子树和右子树，即使只有一棵子树也 要进行区分，说明它是左子树，还是右子树。这是二叉树与树的最 主要的差别，二叉树有5种基本形态

二叉树的基本运算操作：

• 初始化Initiate(BT):建立一棵空二叉树，BT=∅ ∅。
• 求双亲Parent(BT,X):求出二叉树BT上结点X的双亲结点，若X是BT的根或X根本不是BT上的结点，运算结果为NULL。
• 求左孩子Lchild(BT,X)和求右孩子Rchild(BT,X)：分别求出二叉树BT上结点X的左、右孩子；若X为BT的叶子或X补在BT上，运算结果为NULL。
• 建二叉树Create(BT):建立一棵二叉树BT。
• 先序遍历PreOrder(BT):按先序对二叉树BT进行遍历，每个结点被访问一次且仅被访问一次，若BT为空，则运算为空操作
• 中序遍历InOrder(BT):按中序对二叉树BT进行遍历，每个结点被访问一次且仅被访问一次，若BT为空，则运算为空操作。
• 后序遍历PostOrder(BT):按后序对二叉树BT进行遍历，每个结点被访问一次且仅被访问一次，若BT为空，则运算为空操作。
• 层次遍历LevelOrder(BT):按层从上往下，同一层中结点按从左往右的顺序，对二叉树进行遍历，每个结点被访问一次且仅被访问一次，若BT为空，则运算为空操作

二叉树具有下列重要性质：

1、性质1： 在二叉树的第i(i>=1)层上至多有2^(i-1)个 结点。 

2、性质2：深度为k(k>=1)的二叉树至多有(2^k) -1个 结点，最少为2k-1

3、性质3：对任何一棵二叉树，如果其终端结点数为n0(叶子节点n0个)，度为2的结点数为n2，则n0＝n2＋1。 即：叶结点数n0=度为2的结点数n2+1

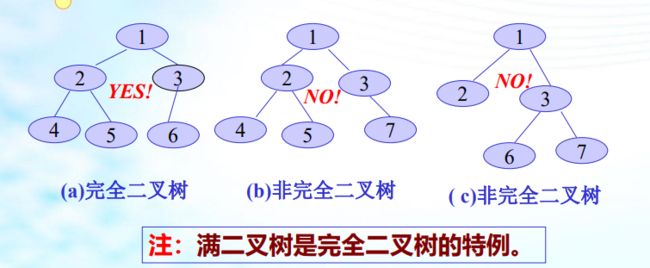
满二叉树：深度为k(k>=1)且有(2^k) -1个结点的 二叉树;满二叉树中结点顺序编号：即从第一层结点开始自上 而下，从左到右进行连续编号。

 

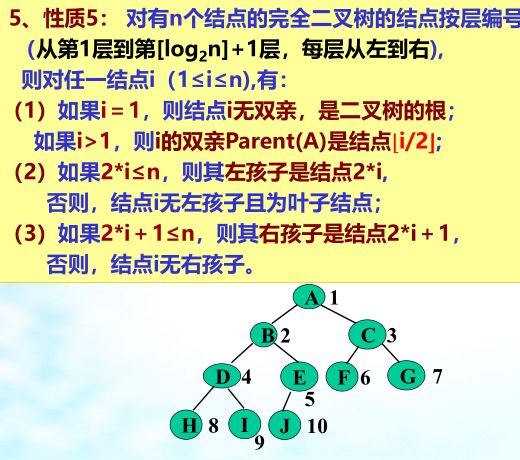
 完全二叉树：深度为K的二叉树中，K-1层结点数是满的2^(k-2)，K层结点是左连续的(即结点编号是连续的)

 

 三、二叉树的存储结构

二叉树通常有两类存储结构：顺序存储结构和链式存储结构。链式存储结构在插入删除结点时较方便，在某些情况下，二叉树的顺序存储结构也很有用

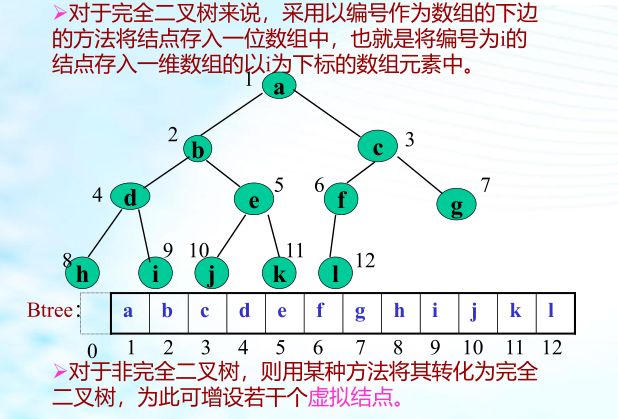
1、二叉树的顺序存储：

 

 完全二叉树的顺序存储：

1. ●节省内存
2. ●结点位置确定方便

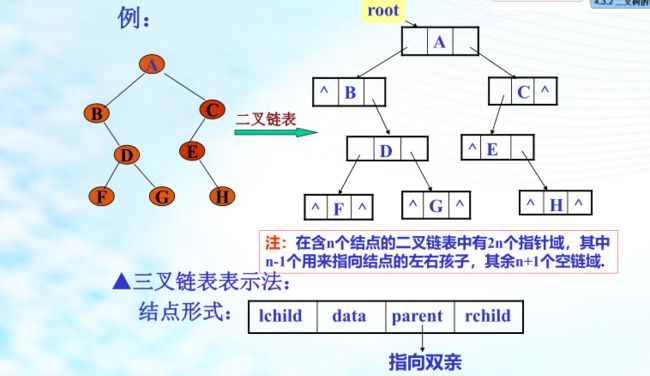
2、二叉树的链式存储结构

 

四、二叉树的遍历

遍历二叉树：是指按某种次序访问二叉树上的所有结点，使每个结点被访问一次且仅被访问一次。

L —— 遍历左子树
D —— 访问根结点
R —— 遍历右子树

1、先序遍历DLR ——首 先 访问 根 结点， 其次 遍历根的 左子树 ， 最后 遍历根 右子树 ，对每棵子树同样按这三步（ 先根、后左、再右 ）进行。
2、中序遍历LDR ——首 先 遍历根的 左子树 ， 其次访问 根 结点， 最后 遍历根 右子树 ，对每棵子树同样按这三步（ 先左、后根、再右 ）进行。
3、后序遍历LRD ——首 先遍历根的 左子树 ， 其次遍历根的右子树 ， 最后 访问 根 结点，对每棵子树同样按这三步（ 先左、后右、最后根 ）进行。

 

 1、先序遍历：ABDECFG

void preorder ( Bintree bt ) {
    /* 先序遍历以 以bt 为根的二叉树*/
    if (bt ！=NULL){
        visit(bt); /* 访问根结点*/
        preorder ( bt->lchild ) ； ；
        preorder ( bt->rchild ) ;
    }
} 

2、中序遍历：DBEAFCG

void inorder (Bintree bt ) {
    /* 中序遍历以bt 为根的二叉树*/
    if (bt ！=NULL){
        inorder ( bt->lchild ) ； ；
        visit(bt); /* 访问根结点*/
        inorder (bt->rchild ) ; 
    } /*…….*/
}

3、后序遍历：DEBFGCA

void postorder (Bintree bt ) {
    /* 后序遍历以bt 为根的二叉树*/
    if (bt ！=NULL){
        postorder ( bt->lchild ) ； ；
        /* 后序遍历以r 的左孩子为根的左子树*/
        postorder ( bt->rchild ) ； ；
        visit(bt);
    }  /* 访问根结点*/
}

 

  二叉树的层次遍历：从二叉树的根结点的这一层开始，逐层向下遍历，在每一层上按从左到右的顺序对结点逐个访问；上图层次遍历：ABCDEFGH

若一棵具有n(n>0)个结点的二叉树的先序序列与后序序列正好相反，则该二叉树一定是高度为n的二叉树(任何节点都没左子树或者任何节点都没右子树)

若一棵具有n(n>0)个结点的二叉树的先序序列与中序序列正好相反，则每个结点的右子树为空

任意一棵二叉树的前序和后序遍历的结果序列中，各叶子结点之间的相对次序关系是都相同

五、遍历二叉树的应用

① 求二叉树中结点的个数 ；
② 求二叉树中叶子结点的个数 ；
③ 求二叉树中度为1 的结点个数 ；
④ 求二叉树中度为2 2 的结点个数 ；
⑤ 求二叉树中非终端结点个数 ；
⑥交换结点左右孩子；
⑦判定结点所在层次；

六、树和森林

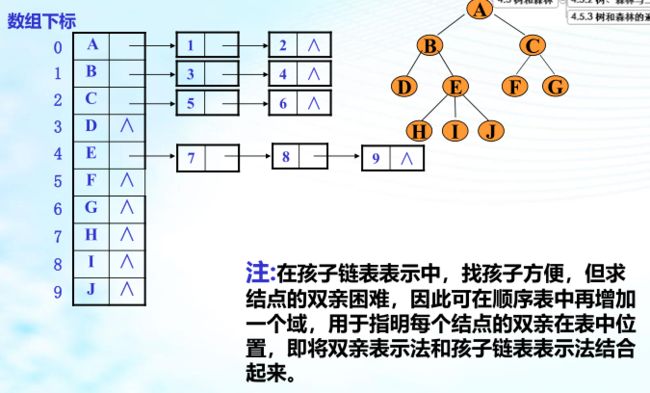
树的存储结构

 

 

 

 

 

一般树转二叉树

 

 

 

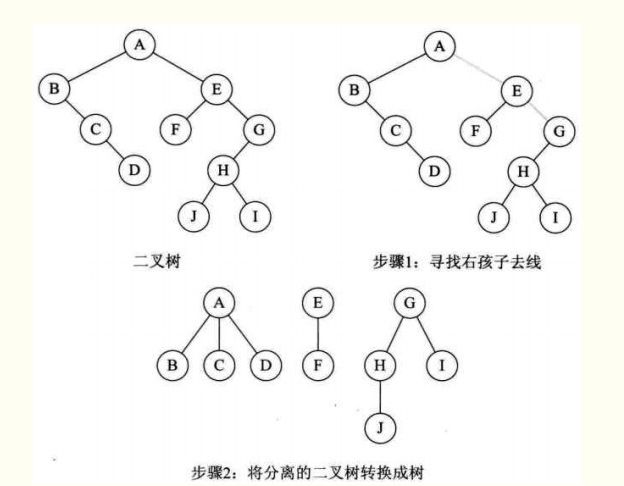
二叉树转换为森林

假如一棵二叉树的根节点有右孩子，则这棵二叉树能够转换为森林，否则将转换为一棵树。

（1）从根节点开始，若右孩子存在，则把与右孩子结点的连线删除。再查看分离后的二叉树，若其根节点的右孩子存在，则连线删除…。直到所有这些根节点与右孩子的连线都删除为止。

（2）将每棵分离后的二叉树转换为树。

 

 七、树和森林的遍历

 

 森林的遍历（注意只有两种）

⚫先序遍历森林：访问森林中每棵树的根结点；先序遍历森林中第一棵树的根结点的子树组成的森林；先序遍历除去第一棵树之外其余的树组成的森林。对下图中森林进行先序遍历的序列为：ABCDEFGHJI
⚫中序遍历森林：中序访问森林中第一棵树的根结点的子树组成的森林；访问第一棵树的根结点；中序遍历除去第一棵树之外其余的树组成的森林；对下图中森林进行先序遍历的序列为：BCDAFEJHIG

 

八、判定树和哈夫曼树

 

路径：在一棵树中，一个结点到另一个结点之间的通路，称为路径。图 1 中，从根结点到结点 a 之间的通路就是一条路径。
路径长度：在一条路径中，每经过一个结点，路径长度都要加 1 。例如在一棵树中，规定根结点所在层数为1层，那么从根结点到第 i 层结点的路径长度为 i - 1 。图 1 中从根结点到结点 c 的路径长度为 3。
结点的权：给每一个结点赋予一个新的数值，被称为这个结点的权。例如，图 1 中结点 a 的权为 7，结点 b 的权为 5。
结点的带权路径长度：指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如，图 1 中结点 b 的带权路径长度为 2 * 5 = 10 。
树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。例如图 1 中所示的这颗树的带权路径长度为：WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3

什么是哈夫曼树

当用 n 个结点（都做叶子结点且都有各自的权值）试图构建一棵树时，如果构建的这棵树的带权路径长度最小，称这棵树为“最优二叉树”，有时也叫“赫夫曼树”或者“哈夫曼树”。
在构建哈弗曼树时，要使树的带权路径长度最小，只需要遵循一个原则，那就是：权重越大的结点离树根越近。在图 1 中，因为结点 a 的权值最大，所以理应直接作为根结点的孩子结点。

哈夫曼树不存在度为1的节点，树形结构不唯一，左右子树没有顺序要求

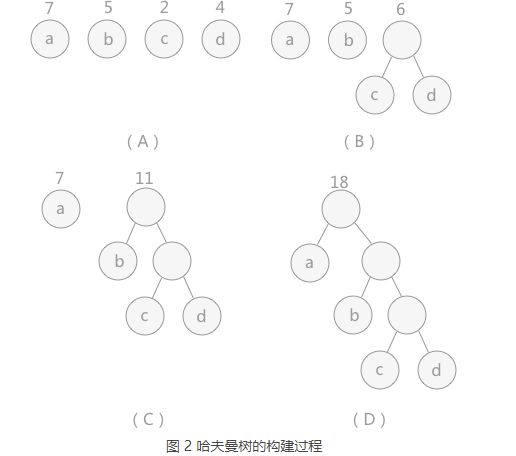
构建哈夫曼树的过程

• 对于给定的有各自权值的 n 个结点，构建哈夫曼树有一个行之有效的办法：
• 在 n 个权值中选出两个最小的权值，对应的两个结点组成一个新的二叉树，且新二叉树的根结点的权值为左右孩子权值的和；
• 在原有的 n 个权值中删除那两个最小的权值，同时将新的权值加入到 n–2 个权值的行列中，以此类推；
• 重复 1 和 2 ，直到所以的结点构建成了一棵二叉树为止，这棵树就是哈夫曼树。

哈夫曼编码：得到哈夫曼树后，自顶向下按路径编号，指向左节点的边编号0，指向右节点的边编号1，从根到叶节点的所有边上的0和1连接起来，就是叶子节点中字符的哈夫曼编码。

 

 

对应的哈夫曼编码分别为：

•  A：111
• B：10
• C：110
• D：0