1. 函数
1.1 函数的定义
量和量之间的关系如:\(A=\pi \mathrm{r}^{2}\)
\(y=f(x)\) 其中 x 是自变量,y 是因变量
函数在 \(x_{0}\) 处取得的函数值 \(y_{0}=\left.y\right|_{x=x_{0}}=f\left(x_{0}\right)\)
符号只是一种表示,也可以 \(y=g(x), y=\varphi(x), y=\psi(x)\)
1.2 函数的分类
分段函数
\(f(x)=\left\{\begin{array}{ll}\sqrt{x}, & x \geq 0 \\ -x, & x<0\end{array}\right.\)
反函数
\(\mathrm{h}=\frac{1}{2} g t^{2} \rightarrow h=h(t) \quad \mathrm{t}=\sqrt{\frac{2 \mathrm{h}}{\mathrm{g}}} \rightarrow t=t(h)\)
相当于把自变量和因变量调换位置,其中右边的函数表示形式就是左边的反函数。
显函数与隐函数
像 \(y=x^{2}+1\) 这种的我们就称之为显函数。
如果它的表达式是 \(F(x, y)=0\) 或者 \(3 x+y-4=0\) 这样需要我们去推导出 y=? 的,我们称为隐函数。
1.3 函数的特性
奇偶性
偶函数 \(f(-x)=f(x)\),比如 \(f(x)=x^{2}\)
奇函数 \(f(-x)=-f(x)\),比如 \(f(x)=x^{3}\)
周期性
\(f(x+T)=f(x)\)
单调性
在变量的取值区间上如果一直是递增或者递减,就是单调函数。
2. 极限
2.1 极限的符号表示
\(x \rightarrow \infty\) 当\(|x|\)无限增大时(负无穷是向左增大)
\(x \rightarrow+\infty\) 当 x 无限增大时
\(x \rightarrow-\infty\) 当 x 无限减小时
\(x \rightarrow x_{0}\) 当 x 从\(x_{0}\)的左右两侧无限接近\(x_{0}\)时
\(x \rightarrow x_{0}^{+}\) 当 x 从\(x_{0}\)的右侧无限接近\(x_{0}\)时
\(x \rightarrow x_{0}^{-}\) 当 x 从\(x_{0}\)的左侧无限接近\(x_{0}\)时
2.2 数列
按照一定次数排列的一组数:\(u_{0},u_{1},u_{2},...u_{n},...\) 其中\(u_{n}\) 叫做通项。
如果数列 \(\{u_{n}\}\) 当 n 无限增大时,其通项无限接近于一个常数 A 时,我们称该数列收敛于 A,否则称该数列为发散。
举例:
\(\lim_{n\rightarrow\infty} u_{n}=A\) 当 n 趋近于无穷大时收敛于 A
\(\lim_{n \rightarrow\infty} \frac{1}{3^{n}}=0\) 当 n 趋近于无穷大时收敛于 0
\(\lim_{n\rightarrow\infty} 2^{n}\) 当 n 趋近于无穷大时,极限不存在,是发散的
\(\lim_{x \rightarrow1} \frac{(x^{2}-1)}{x-1}\) = \(\lim_{x \rightarrow1} \frac{(x+1)(x-1)}{x-1}\) = 2
如果一个函数,在左右邻域都有定义时,那求极限时需要考虑左右极限的问题:
\(f(x)=\left\{\begin{array}{cc}x-1 & x<0 \\ 0 & x=0 \\ x+1 & x>0\end{array}\right.\)
\(\lim _{x \rightarrow 0^{+}} f(x)=\lim _{x \rightarrow 0^{+}}(x+1)=1\)
\(\lim _{x \rightarrow 0^{-}} f(x)=\lim _{x \rightarrow 0^{-}}(x-1)=-1\)
显然,它的左右极限都是存在的,但是不相等,所以\(\lim _{x \rightarrow 0} f(x)\)不存在。
2.3 无穷小与无穷大
以 0 为极限,\(\lim_{x \rightarrow\infty} \frac{1}{x}=0\) 可以看出当 x 趋近于无穷大时收敛于 0,我们可以称\(\frac{1}{x}\)是\({x \rightarrow\infty}\)时的无穷小。
这里有些基本性质需要记住:
- 有限个无穷小的代数和仍是无穷小。
- 有限个无穷小的积仍是无穷小。
- 有界变量与无穷小的积仍是无穷小
- 无限个无穷小之和不一定是无穷小。
- 无穷小的商不一定是无穷小。
以\(\infty\)为极限,\(\lim_{x \rightarrow{x_{0}}} {f(x)}=\infty\)
注意:无穷大并不是指一个很大的值,而是针对变量的变换过程而言的;如果在一组变换中,\(f(x)\)为无穷大,那么\(\frac{1}{f(x)}\)是无穷小。
2.4 函数的连续性
\(\lim_{\Delta x \rightarrow 0} \Delta y=\lim _{\Delta x \rightarrow 0}\left[f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right)\right]=0\)
设函数\(y=f(x)\)在点 \({x_{0}}\) 的某邻域内有定义时,那么当\(\Delta x\)变化趋近于 0 时,\(\Delta y\)也为 0,我们称函数\(y=f(x)\)在点 \({x_{0}}\) 处连续。
连续需要满足的条件:
- 函数在该点处有定义
- 函数在该点处极限\(\lim_{\Delta x \rightarrow 0}f(x)\)存在
- 极限值等于函数值\(f(x_{0})\)
有连续就有间断,我们称之为间断点(了解概念就行)。
3. 导数
3.1 导数的定义
假设汽车运动的速度为 v,路程为 s,耗费的时间为 t,那么在单位时间内它的平均速度可以表示为\(\bar{v}=\frac{\Delta \mathrm{s}}{\Delta \mathrm{t}}=\frac{\mathrm{s}\left(\mathrm{t}_{0}+\Delta t\right)-s\left(t_{0}\right)}{\Delta t}\)
当\(\lim_{\Delta t \rightarrow 0}\)时,也就是求极限可以得到它的瞬时速度表示\(v\left(t_{0}\right)=\lim _{\Delta t \rightarrow 0} \bar{v}=\lim _{\Delta \rightarrow 0} \frac{\Delta \mathrm{s}}{\Delta \mathrm{t}}=\lim _{\Delta t \rightarrow 0} \frac{s\left(t_{0}+\Delta t\right)-s\left(t_{0}\right)}{\Delta t}\)
这个其实也称为平均变化率的极限,如果这个值它是存在的,那么我们称此极限是函数\(s=f(t)\)在点\(t_{0}\)处的导数 \(f^{\prime}(x_{0})\),也可以表示为\(\left.y^{\prime}\right|_{x=x_{0}}\)
导数的实质:增量比的极限。
3.2 偏导数
上面导数的定义中只有一个自变量,如果我们的自变量不再是一个,而是有多个 x,y,z..呢,也就是多元函数?一般而言,固定其中一个变量(假设这个变量在求导过程中方向不会变),而求另外一个自变量的导数,这种操作就叫做求偏导。举个栗子:
求函数\(f(x, y)=x^{2}+3 x y+y^{2}\)在点(1,2)处的偏导数?
思路:因为有两个自变量,所以会求出两个偏导数,当然前提是它们在邻域内都是可导的。
先固定 y,得到\(f_{x}(x, y)=2 x+3 y\)
固定 x,得到\(f_{y}(x, y)=3 x+2 y\)
所以:
\(f_{x}(1,2)=\left.(2 x+3 y)\right|_{x=1 \atop y=2}=8\)
\(f_{y}(1,2)=\left.(3 x+2 y)\right|_{x=1 \atop y=2}=7\)
可以看出,偏导数只是沿着 x 轴或者 y 轴的变化。
3.3 方向导数
方向导数的定义
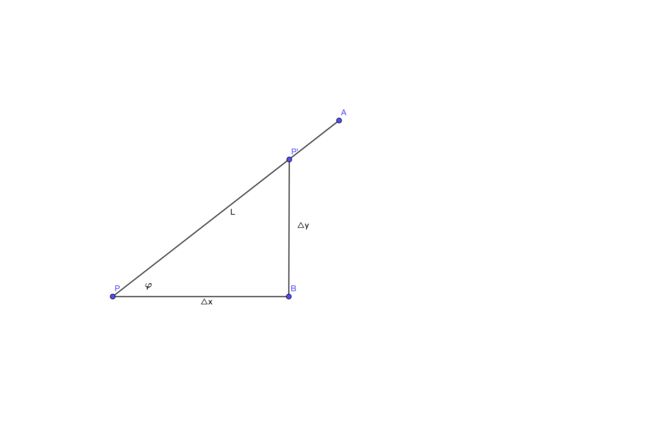
如上图示,先定义一个函数\(z=f(x,y)\),两点之间的距离(模),\(\left|P P^{\prime}\right|=\rho=\sqrt{(\Delta x)^{2}+(\Delta y)^{2}}\),如果函数的增量\(\Delta z=f(x+\Delta x, y+\Delta y)-f(x, y)\)与这两点的距离比例存在,则称此为 P 点沿着 L 方向的方向导数
\(\frac{\partial f}{\partial l}=\lim _{\rho \rightarrow 0} \frac{f(x+\Delta x, y+\Delta y)-f(x, y)}{\rho}\)
其实:一个点在一个平面上(这个平面就是这个点的切面)是有无数个方向的,并不是一定沿着坐标轴的。
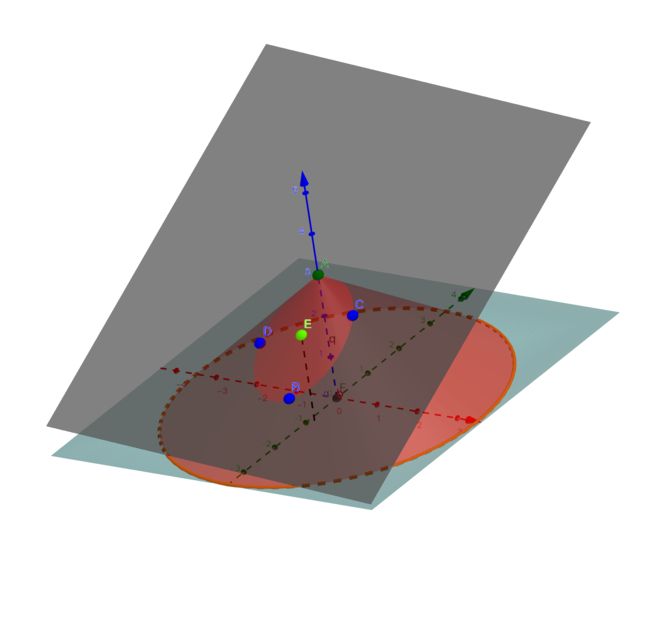
可以看到图中由 BCD 构建的平面切于函数,在此切面上有一点 E,E 点在此切面 q上是有无数(360°)个方向(L),即对于一个点方向导数是很多的。
(二维里一个点确定一条切线,三维里一条线确定一个切面,这个线上随便取一个点,沿着这个点在平面上又能画出无数个线)
方向导数与偏导数的关系
如果函数\(z=f(x,y)\)在点\(P(x,y)\)是可微分的,那么该点沿任意方向 L 的方向导数都是存在的。同时,我们可以得出它与偏导数的关系,其中\(\varphi\)为X 轴到L 的角度。
\(\frac{\partial f}{\partial l}=\frac{\partial f}{\partial x} \cos \varphi+\frac{\partial f}{\partial y} \sin \varphi\)
3.4 梯度
直白的解释一下:在下山过程中怎么样下山是最有效率,肯定是沿着你所在位置求一个切线的方向,切线有两个方向,一个是向上一个是向下。那么梯度就是向上的方向(只要记住梯度本身是上升的)。在机器学习中,通常我们优化的方向是梯度下降,其实就是沿着梯度反方向就行了。
梯度和方向导数的关系:方向导数是随意的,梯度是方向导数中值取得最大的那个方向。
参考资料
1)曲线切线的定义和导数
2)方向导数与梯度