学SPFA已经有一段时间了,还没有学他最原始的算法版本,于是这里就补一个Bellman-Ford算法吧。
这是一个解决单源无负环最短路的算法
主要思想
- 我们知道要让图联通,每一个点必须有一条边相连。
- 我们每次取一个点取延申,不断地得到最优的路劲。同时如果没有负环存在的情况下,我们的最终拓展边数将会是n - 1。也就是遍历n - 1次边
例子
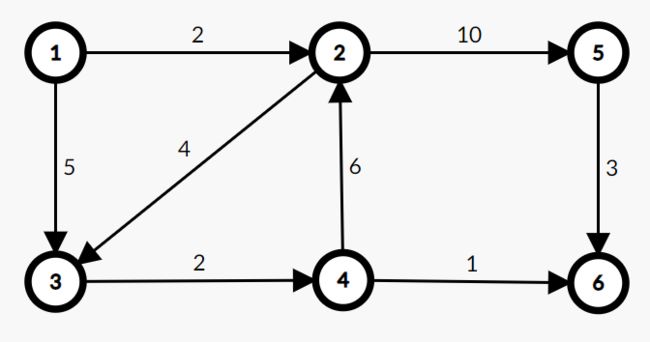
共有8条有向边
- 1 2 2
- 1 3 5
- 2 3 4
- 2 5 10
- 3 4 2
- 4 2 6
- 4 6 1
- 5 6 3
我们取点1作为出发边,求从点1到其他边的距离
有dis数组, dis[6] = {0, INF, INF, INF, INF, INF}
第一遍遍历, dis[6] = {0, 2, 5, INF, INF, INF}
第二遍遍历, dis[6] = {0, 2, 5, 7, 12, INF}
第三遍便利, dis[6] = {0, 2, 5, 7, 12, 8},这里得到了所有点到点1的最短路。而且遍历次数是小于n的。
我们假设一种最极端的例子,路径中只有一条路,也就是每个点都只连着一条路,这里的遍历次数是最多的要(n - 1)次
求最短路的关键代码
//Powered by CK 2020:04:06
int from[N], to[N], value[N], dis[N], n, m;//分别是出发点,终点,边权值,到点1的距离,点数,边数。
void Bellman_Ford() {
for(int i = 1; i <= n; i++) dis[i] = INF;
dis[1] = 0;
while(true) {
bool can_shorted = true;
for(int i = 0; i < m; i++) {
if(dis[to[i]] > dis[from[i]] + value[i]) {//遍历一遍下来可以使边缩小,标记can_shorted标记。
dis[to[i]] = dis[from[i]] + value[i];
can_shorted = false;
}
}
if(can_shorted) break;
}
}
判断是否存在负边权的代码
//Powered by CK 2020:04:06
int from[N], to[N], value[N], dis[N], n, m;
bool Bellman_Ford() {
for(int i = 1; i <= n; i++) dis[i] = INF;
dis[1] = 0;
for(int j = 0; j < n)
for(int i = 0; i < m; i++) {
if(dis[to[i]] > dis[from[i]] + value[i]) {
dis[to[i]] = dis[from[i]] + value[i];
if(j == n - 1) return true;//上面已经说明的,如果不存在负边权,不可能可以到一个点两次。
}
}
}
return false;
}
复杂度分析
n * m, 但是通过上面的例子可以分析,到n * m一般不可能,真实的结果使比这个稍微小的。