由于当年的百度空间和网易博客上发布的内容都因为这两个博客的停止维护都不在啦,现在上了大学,就读的也是计算机专业,有些舍不得以前在这两个博客上发的文章,就只好手动搬家过来这边啦~ 希望能够帮助到正在学习信息学竞赛的同学们哦~ 哈哈哈,有些内容毕竟是高中时代写的,还有些稚嫩,还请大家多多包涵哦。
RMQ问题,即Range Maximum/Minimum Query(区间最值查询问题),指对于一个有序序列,回答若干区间的数值最值的查询。
注:下面贴出代码均只支持查询。
主要算法(或数据结构):
1.线段树:
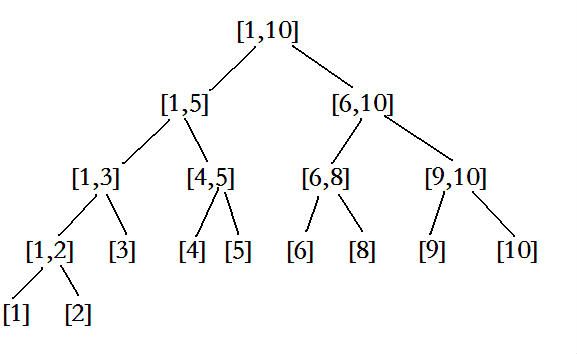
一种二叉搜索树,其每个节点均为一个区间,支持大多数快速区间操作,查询,如区间[1,10]建树如下:
时间复杂度: 预处理O(n), 查询O(log n) 总复杂度O(n+q log n)
空间复杂度:O(n) (常数较大)
优点:容易理解,编写,适用范围广
缺点:在支持区间修改操作时代码较长。
代码(指针,较慢):
#include
#include
using namespace std;
#define MAXN 100001
struct node {
node *left,*right;
int l,r,max;
};
node *roof;
int n,m;
int a[MAXN];
int Build(int l,int r,node *p){
(*p).l=l;
(*p).r=r;
if (l==r){
(*p).left=(*p).right=NULL;
(*p).max=a[l];
return 0;
}
Build(l,(l+r)>>1,(*p).left=new(node));
Build(((l+r)>>1)+1,r,(*p).right=new(node));
(*p).max=max((*(*p).left).max,(*(*p).right).max);
return 0;
}
int get_max(int l,int r,node *p){
if (l==(*p).l&&r==(*p).r){
return (*p).max;
}
int mid=((*p).l+(*p).r)>>1;
if (r<=mid){
return get_max(l,r,(*p).left);
}
if (l>mid){
return get_max(l,r,(*p).right);
}
return max(get_max(l,mid,(*p).left),get_max(mid+1,r,(*p).right));
}
int main(){
scanf("%d%d",&n,&m);
for (int i=0;i++ 之前去膜拜了ZKW大神的线段树,结果看了半天都没弄懂自底向上的线段树,所以自己写了一个从中间查询的代码,用一个辅助数组first[i]来储存以i为左端点的区间节点,从中间开始查找覆盖区间,速度还可以(就是遇到区间修改就悲剧了)
代码2:
#include
#include
#include
#include
using namespace std;
#define MAXN 100001
struct node {
int l,r,max;
} t[MAXN*5];
int a[MAXN];
int n,m;
int first[MAXN];
void Build(int l,int r,int rank){
if (!first[l]){
first[l]=rank;
}
t[rank].l=l;
t[rank].r=r;
if (l==r){
t[rank].max=a[l];
return ;
}
int mid=(l+r)>>1,left=rank<<1,right=left^1;
Build(l,mid,left);
Build(mid+1,r,right);
t[rank].max=max(t[left].max,t[right].max);
}
int getmax(int l,int r){
int rec=0,i=l;
while (i<=r){
int j=first[i];
while (t[j].r>r) j=j<<1;
rec=max(rec,t[j].max);
i=t[j].r+1;
}
return rec;
}
int main(){
memset(first,0,sizeof(first));
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
scanf("%d%d",&n,&m);
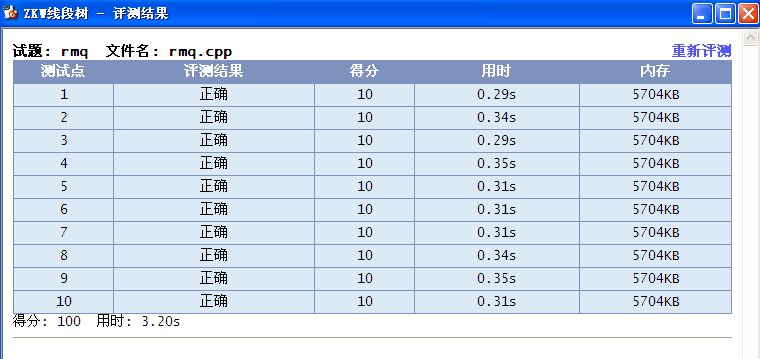
for (int i=0;i++ 花了好几天终于把ZKW线段树膜拜完了~~,速度超快,常数真的很小。。。不废话了,贴代码:
#include
#include
using namespace std;
#define MAXN 200000
#define MAXD 20
#define D 1
struct node {
int l,r,max;
} tree[MAXN*2];
int z[MAXD];
int N,n,m,M;
int a[MAXN];
void Build(int l,int r,int t){
tree[t].l=l;
tree[t].r=r;
if (l==r){
tree[t].max=a[l];
if (l==1){
M=t-1;
}
return ;
}
Build(l,(l+r)>>1,t<<1);
Build(((l+r)>>1)+1,r,(t<<1)^1);
tree[t].max=max(tree[t<<1].max,tree[(t<<1)^1].max);
}
int getmax(int l,int r){
int rec=0;
l--,r++;
l+=M,r+=M;
while ((l^r)!=1){
if (!(l&1)) rec=max(rec,tree[l^1].max);
if (r&1) rec=max(rec,tree[r^1].max);
l>>=1;
r>>=1;
}
return rec;
}
int main(){
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
z[0]=1;
for (int i=0;i++ 2.树状数组(Binary Index Tree)。
树状数组是线段树一种小巧的替代品,也支持某一些区间查询修改操作(如:区间求和,RMQ等)
预备函数:lowbit (x) = ((~x)+1)&x
建立:若以T[]为索引数组,则t[i]表示区间[i-lowbit(i)+1,i] 。索引数组表示区间如下(如表示[1,10]):
查询:从i=r开始扫描,如果区间[i-lowbit(i)+1,i] 在查询区间内,则ans=max/min(ans,t[i]) i=i-lowbit(i) 否则 ans=max/min(ans,a[i]) i-- 知道整个区间扫面完成为止。
时间复杂度:预处理:O(n)或O(n log n) 查询:O(log^2 n) 总复杂度:O(n + q log^2 n)或O(n log n + q log^2 n)
空间负责度:O (n)(常数较小)
优点:节省空间,代码简短,常数小
缺点: 查询复杂度较高,在支持修改情况下复杂度较高,使用范围较小.
代码:
#include
#include
using namespace std;
#define MAXN 100001
int lowbit(int x){
return ((~x)+1)&x;
}
int t[MAXN];
int a[MAXN];
int n,m;
int get_max(int l,int r){
int rec=-0x7fffffff;
if (!r){
return rec;
}
int i=r;
while (i>=l){
int j=i-lowbit(i)+1;
if (j>=l){
rec=max(rec,t[i]);
i=j-1;
} else {
rec=max(rec,a[i]);
i--;
}
}
return rec;
}
int main(){
scanf("%d%d",&n,&m);
for (int i=0;i++ 3.ST算法:
该算法以倍增思想为基础,支持离线RMQ问题。
大意:
定义f[i][j]表示区间[i,i+2^j-1]
构建时使用动态规划思想:
f[i][j]=max/min(f[i][j-1] ,f[i+2^(j-1)][j-1])
对于某区间[l,r]支持O(1)RMQ查询
k=int(log10(r-l+1)/log10(2))
max (l,r)=max(f[l][k],f[r-EXP[k]+1][k])
空间复杂度:O(n log n)
时间复杂度:预处理O(n log n) 查询O(1) 总复杂度:O(n log n + q)
优点:代码简洁,快速
缺点:无法支持修改操作
代码:
#include
#include
#include
using namespace std;
#define MAXN 100001
int f[MAXN][20];
int a[MAXN];
int EXP[20];
int m,n;
int main(){
EXP[0]=1;
for (int i=0;i++<19;){
EXP[i]=EXP[i-1]*2;
}
scanf("%d%d",&n,&m);
for (int i=0;i++ 4.将RMQ转LCA问题解决
建立Cartesian Tree,将区间问题转为树上的LCA(最近公共祖先问题解决)。LCA可用在线算法O(q log n)或Tarjan O(q)解决
空间复杂度:O(n)
时间复杂度:O(n+q)
优点:复杂度低
缺点:在有元素重复情况下较为麻烦,使用递归编写容易栈溢出
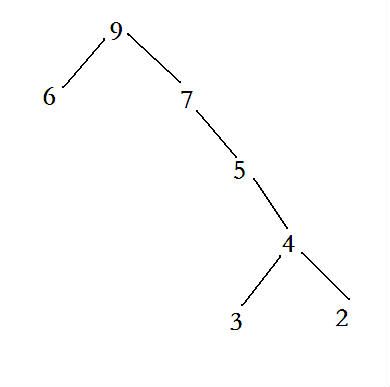
注:Cartesian Tree
如:对于某序列6 9 7 5 3 4 2建树如下:
此时,某个区间[l,r]的最值,即l,r在树上对应元素的LCA的权.
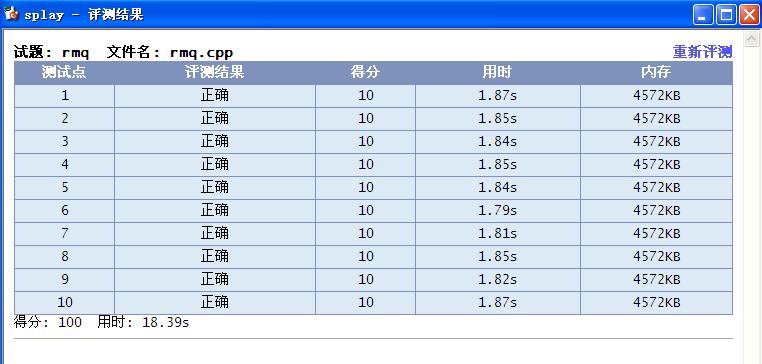
5.splay(伸展树)维护区间求RMQ
用数列建立splay,关键字为某权值在序列中的位置,splay的某个节点上顺便储存以该节点为根的子树的权值最值,在进行splay(),ratote()的时候顺便维护,查询区间[l,r]时用splay()将关键字l-1的节点提到根,将关键字r+1的节点提到根的右子树,那么,查询结果就是根右子树的左子树上维护的信息。(注意,在序列中要另加两个节点0和n+1以便维护)
空间复杂度:O(n)
时间复杂度:O(q log n)(平摊)
优点:方便,支持区间插入,翻转,删除等线段树难以实现的操作。
缺点:时间常数较大。
代码:
#include
#include
#include
using namespace std;
#define MAXN 100010
int a[MAXN];
struct node {
int t,MAX;
node *left,*right;
};
node *roof,*bank=new(node);
int n,m;
void zag(node* &t) {
node*k=t->right;
t->right=k->left;
t->MAX=max(max(t->left->MAX,t->right->MAX),a[t->t]);
k->left=t;
k->MAX=max(max(k->left->MAX,k->right->MAX),a[k->t]);
t=k;
}
void zig(node* &t) {
node*k=t->left;
t->left=k->right;
t->MAX=max(max(t->left->MAX,t->right->MAX),a[t->t]);
k->right=t;
k->MAX=max(max(k->left->MAX,k->right->MAX),a[k->t]);
t=k;
}
void Merge(node *u,node* &t,bool flag) {
if (!t) {
t=u;
return ;
}
if (flag) {
t->left=u;
t->MAX=max(t->MAX,u->MAX);
zig(t);
}else {
t->right=u;
t->MAX=max(t->MAX,u->MAX);
zag(t);
}
}
void splay(int k,node* &t) {
node*l=NULL,*r=NULL;
while (t!=bank&&t->t!=k) {
if (kt) {
if(t->left!=bank&&kleft->t) {
zig(t);
}
node*u=t->left;
t->MAX=max(t->right->MAX,a[t->t]);
t->left=bank;
Merge(t,r,true);
t=u;
} else {
if(t->right!=bank&&k>t->right->t) {
zag(t);
}
node*u=t->right;
t->MAX=max(t->left->MAX,a[t->t]);
t->right=bank;
Merge(t,l,false);
t=u;
}
}
node*u;
if (l) {
u=t->left;
t->left=l;
l->right=u;
l->MAX=max(l->MAX,u->MAX);
}
if (r) {
u=t->right;
t->right=r;
r->left=u;
r->MAX=max(r->MAX,u->MAX);
}
t->MAX=max(max(t->left->MAX,t->right->MAX),a[t->t]);
}
void INSERT(int k) {
node*t=roof,*T=NULL;
bool flag;
while (t!=bank) {
T=t;
if (kt) flag=false,t=t->left
; else flag=true,t=t->right;
}
t=new(node);
t->left=t->right=bank;
t->MAX=a[k];
t->t=k;
if (T) {
if (flag) T->right=t
; else T->left=t;
} else roof=t;
}
int main() {
freopen("input.txt","r",stdin);
freopen("output.txt","w",stdout);
scanf("%d%d",&n,&m);
for (int i=0;i++MAX=a[0]=a[n+1]=-0x7fffffff;
roof=bank->left=bank->right=bank;
for (int i=0;i<=n+1;i++) {
INSERT(i);
splay(i,roof);
}
while (m--) {
int l,r;
scanf("%d%d",&l,&r);
splay(l-1,roof);
splay(r+1,roof->right);
printf("%d\n",roof->right->left->MAX);
}
fclose(stdin);fclose(stdout);
return 0;
}
附:以上各代码效率(100000*100000):
本人乃弱菜一只,以上内容如有不当之处,敬请之处。