叶璃O

DS博客作业02--栈和队列

0.PTA得分截图

1.本周学习总结（0-4分）

1.1 总结栈和队列内容：

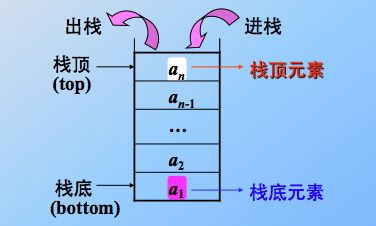
1.1.1 栈

栈的定义：
栈的本质还是线性表：限定仅在表尾进行插入或删除操作。俗称：后进先出，也可说是先进后出。
栈的声明（栈的声明有两种）：
第一种：

typedef struct sta
{
    int stack[SIZE];    /* 存放栈中元素的一维数组 */
    int top;            /* 存放栈顶元素的下标 */
}stack;

第二种：

typedef struct sta
{
    int *top;            /* 栈顶指针 */
    int *bottom;        /* 栈底指针 */
    int stack_size;        /* 栈的最大容量 */
}stack;

栈的分类：
与线性表同样的，栈也分为顺序和链式两大类。其实和线性表大同小异，只不过限制在表尾进行操作的线性表的特殊表现形式。
顺序栈：
利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素，同时附设指针 top 指示栈顶元素在顺序栈中的位置，附设指针 base 指示栈底的位置。同样，应该采用可以动态增长存储容量的结构。且注意，如果栈已经空了，再继续出栈操作，则发生元素下溢，如果栈满了，再继续入栈操作，则发生元素上溢。栈底指针 base 初始为空，说明栈不存在，栈顶指针 top 初始指向 base，则说明栈空，元素入栈，则 top++，元素出栈，则 top--，故，栈顶指针指示的位置其实是栈顶元素的下一位（不是栈顶元素的位置）。
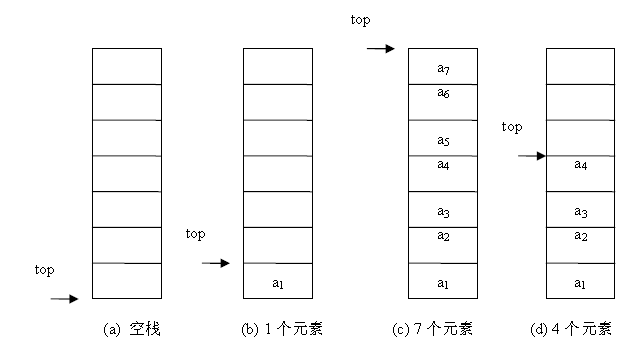
链式栈：
其实就是链表的特殊情形，一个链表，带头结点，栈顶在表头，插入和删除（出栈和入栈）都在表头进行，也就是头插法建表和头删除元素的算法。显然，链栈还是插入删除的效率较高，且能共享存储空间。

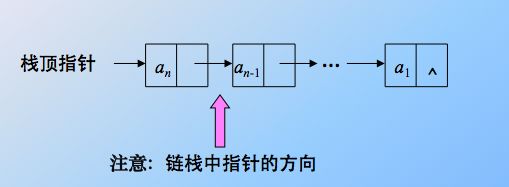
是栈顶在表头！栈顶指针指向表头结点。栈底是链表的尾部，base 就是尾指针。还有，理论上，链式结构没有满这一说，但是理论上是这样的，也要结合具体的内存，操作系统等环境因素。
栈的基本操作函数(仅针对顺序栈)：
- InitStack(&s)：初始化栈。构造一个空栈s。
  函数实现：

void InitStack(SqStack &s)
{  s=new Stack;     
    s->top=-1;
}

DestroyStack(&s)：销毁栈。释放栈s占用的存储空间。
函数实现：

void DestroyStack(SqStack &s)
{
　　delete s;
}

StackEmpty(s)：判断栈是否为空:若栈s为空，则返回真（1）；否则返回假（0）。
函数实现：

bool StackEmpty(SqStack s)
{
　　return(s->top==-1);
}

Push(&S，e)：进栈。将元素e插入到栈s中作为栈顶元素。
函数实现：

bool Push(SqStack &s,ElemType e)
{
　 if (s->top==MaxSize-1)  
    return false;
   s->top++;           //栈顶指针增1
   s->data[s->top]=e;     
   return true;
}

Pop(&s，&e)：出栈。从栈s中退出栈顶元素，并将其值赋给e。
函数实现：

bool Pop(SqStack &s,ElemType &e)
{
   if (s->top==-1)  //栈为空的情况，栈下溢出
    return false;
   e=s->data[s->top];//取栈顶指针元素     
   s->top--;        //栈顶指针减1
   return true;
}

GetTop(s，&e)：取栈顶元素。返回当前的栈顶元素，并将其值赋给e。
函数实现：

bool GetTop(SqStack *s,ElemType &e)
{   
　  if (s->top==-1)  //栈为空的情况    
    return false;
    e=s->data[s->top];      
    return true;
}

栈的头文件(C++):stack操作模板：

#include
1.stack  s:初始化栈，参数表示元素类型。//后续的函数引用你的初始化
2.s.push(t):入栈元素t。
3.s.top()：返回栈顶元素。
4.s.pop()：出栈操作只是删除栈顶元素，并不返回该元素。
5.s.empty()，当栈空时，返回true。
6.s.size()：访问栈中的元素个数。

栈的应用：
- 字符匹配：在C语言中有一些符号是成对匹配出现的，利用栈可以实现类似编译器括号是否匹配的能力。
- 小型计算器的实现：将中缀表达式转后缀表达式。
- 十进制正整数N进制：进制转换可以用很多方法来实现，其中也能用栈的方式实现。

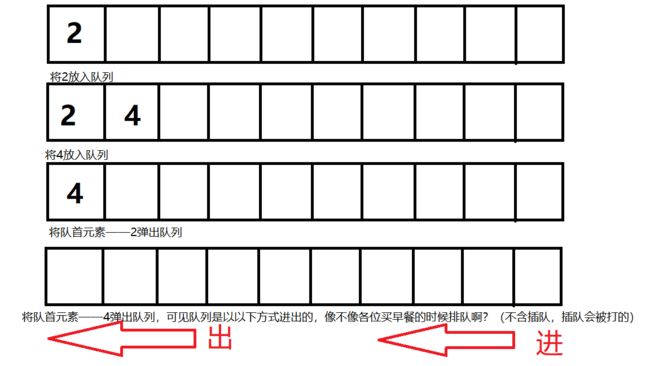
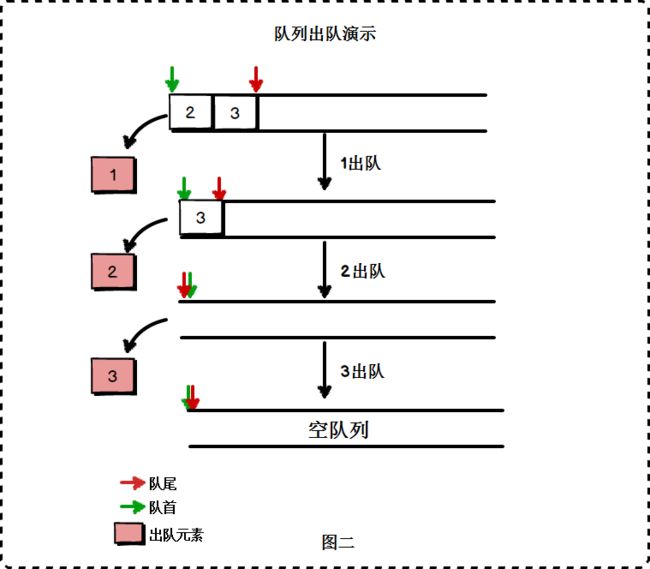
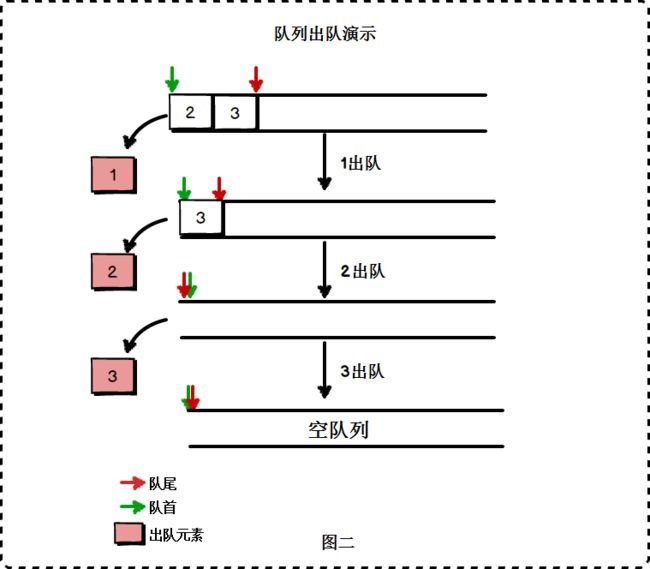
1.1.2 队列

队列的定义：
只允许在表的一端进行插入，而在表的另一端进行删除的线性表。
队列的声明：

struct QNode {
    ElementType *Data;  /* 存储元素的数组   */
    Position Front;     /* 队列的头指针     */
    int Count;          /* 队列中元素个数   */
    int MaxSize;        /* 队列最大容量     */
};

队列的基本操作函数：
- InitQueue(&Q)：构造一个空队列Q。
  函数实现：

void InitQueue(SqQueue *&Q){  
    Q=(SqQueue *)malloc(sizeof(SqQueue));  
    Q->front=Q->rear=-1;  
}

DestroyQueue(&Q)：销毁队列Q。
函数实现：

void DestroyQueue(SqQueue *&Q){  
    free(Q);  
}

QueueEmpty(Q)：判断队列Q是否为空。
函数实现：

void QueueEmpty(SqQueue *Q){  
    return (Q->front==Q->rear);  
}

EnQueue(&Q, e)：插入元素e为Q的新的队尾元素。
函数实现：

bool EnQueue(SqQueue *&Q,ElemType e){    
    if(Q->rear==MaxSize) return false;   //队满上溢   
    Q->rear++;    
    Q->data[Q->rear]=e;    
    return true;    
}

DeQueue(&Q, &e)：删除Q的队头元素，并用e返回其值。
函数实现：

bool EeQueue(SqQueue *&Q,ElemType &e){  
    if(Q->front==Q->rear) return false;  
    Q->front++;  
    e=Q->data[Q->front];  
    return true;  
}

1.2.谈谈你对栈和队列的认识及学习体会。

学习了栈和队列，发现两个本质上都是线性表，两者的功能上相似的地方，也有不同的地方。它们都可以用线性表的顺序存储结构来实现，但都存在着顺序存储的一些弊端。
在对栈和队列的学习中，扩展了眼界，对一些题目有了新的理解，如线性表中6-8 jmu-ds-链表倒数第m个数，如果这题用栈或者队列来编译，将更容易，时间复杂度上将更低，这或许就是算法学习的意义：找到时间复杂度更低的算法来实现要求。
在对栈和队列的学习后，了解了日常网络中有很多的事情都是可以通过栈和队列实现的，例如网页的返回，就是通过可以栈来实现的。

2.PTA实验作业（0-2分）

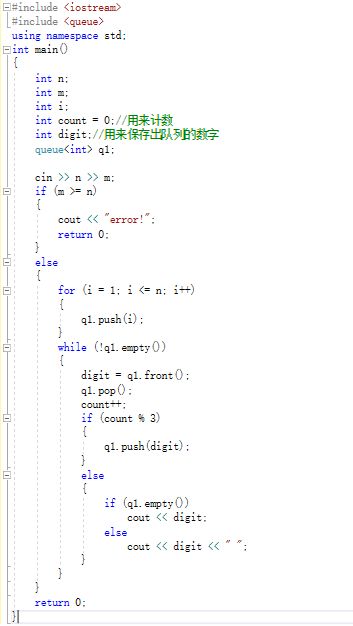
2.1 7-6 jmu-报数游戏 (15分)

2.1.1 代码截图

2.1.2 本题PTA提交列表说明。

Q1:编译错误
A1：再次将C++按C提交
Q2：部分正确
A2：m>=n的点题目要求输出为error！但我输出为error

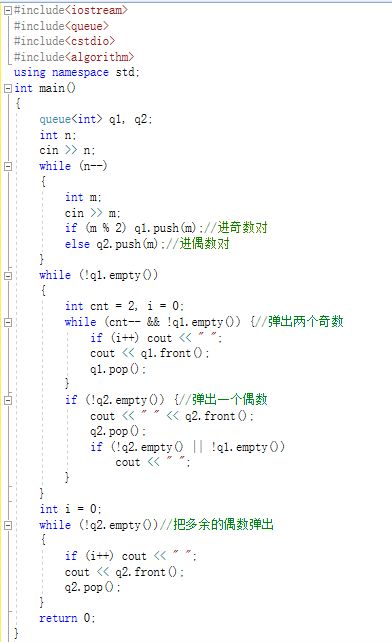
2.2 7-7 银行业务队列简单模拟

2.2.1 代码截图

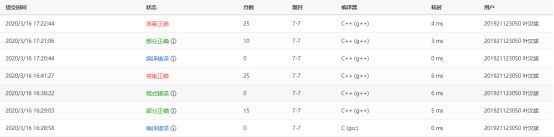
2.2.2 本题PTA提交列表说明。

Q1：编译错误
A1：将C++按C提交
Q2：部分正确
A2：用了多个while导致运行超时
Q3：格式错误
A3：将while删除几个重新编译，但空格没掌握好
Q4：答案正确
A4：将空格处理了一下，虽然PTA对了，但我发现我自己输入3个数（两奇一偶）中最后一个偶数后还有空格
Q5：编译错误
A5：在上一个代码中加上if判断但用q.empty代码后没加小括号
Q6：部分正确
A6：加上一个限定条件后运行发现如果奇数数列不为空时，最后一个偶数和它之后的奇数键没有空格，所以我加在加上了判断奇数数列是否为空的条件，不仅PTA过了，我自己加的测试点也过了

3.阅读代码（0--4分）

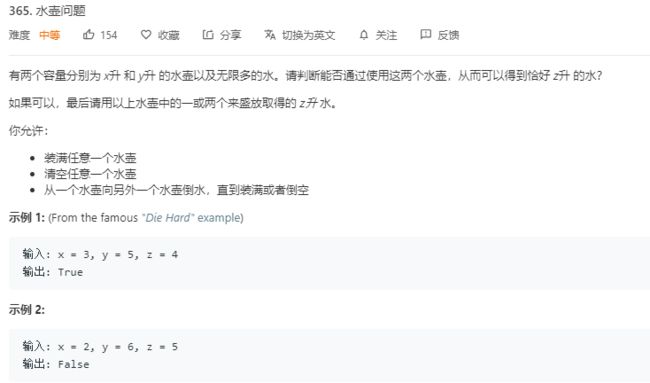
3.1 题目及解题代码

解题代码：

class Solution {
public:
    bool canMeasureWater(int x, int y, int z) {
        // assumed if z = a * x  + b * y, then return true; otherwise, gives false
        // if x = t1 * __gcd(x,y), y = t2 * __gcd(x,y);
        // z = __gcd(x,y) *  (a * t1 + b * t2) ==> z % __gcd != 0 ==> false
        // x = 3, y = 5, z = 4  ===> z = -1 * x + 2 * y
        // x = 2, y = 6, z = 5  ===> failed
        if (z < 0 || x + y < z) return false;
        if (x == z || y == z || x + y == z) return true;
        return z % __gcd(x, y) == 0; 
    
    }
};

3.1.1 该题的设计思路

将本问题转化为ax+by=z是否有解，
定理：a b x y 均为整数，如果ax+by=z有解，那么z一定是gcd(a,b)的倍数，否则无解。//gcd(a,b)函数为求a和b的公约数的函数
时间复杂度为：O(log(min(x,y))，取决于计算最大公约数所使用的辗转相除法。
空间复杂度为：O(1)

3.1.2 该题的伪代码

if z小于0或者x+y小于z then
   返回false
if x等于z或y等于z或x+y等于z then
   返回true
返回 z是否对x和y的公约数的倍数//即是返回true，否返回false

3.1.3运行结果

3.1.4 分析该题目解题优势及难点。

解题优势：该题的设计思路通俗易懂，但凡有点数学基础都能立马通过该解题思路理解复杂的题干要求，在计算最大公约数小的情况加该题的时间复杂度会相对更低。
难点：如果没想到求z和x，y最大公约数的关系，将会不容易下手，并且可能会陷入僵局。计算最大公约数所使用的辗转相除法大的话，时间复杂度相应增大。

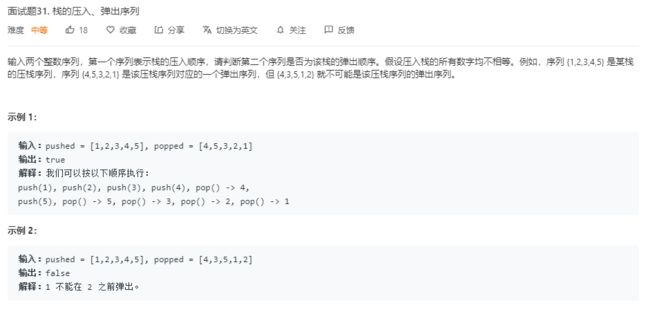
3.2 题目及解题代码