LeetCode 1254. Number of Closed Islands

1、原题描述：

Given a 2D grid consists of 0s (land) and 1s (water).  An island is a maximal 4-directionally connected group of 0s and a closed island is an island totally (all left, top, right, bottom) surrounded by 1s.

Return the number of closed islands.

 

Example 1:

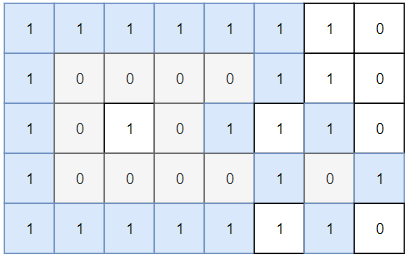
Input: grid = [[1,1,1,1,1,1,1,0],[1,0,0,0,0,1,1,0],[1,0,1,0,1,1,1,0],[1,0,0,0,0,1,0,1],[1,1,1,1,1,1,1,0]]
Output: 2
Explanation: 
Islands in gray are closed because they are completely surrounded by water (group of 1s).

Example 2:

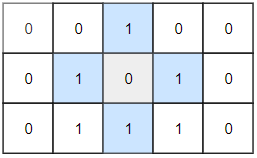
Input: grid = [[0,0,1,0,0],[0,1,0,1,0],[0,1,1,1,0]]
Output: 1

Example 3:

Input: grid = [[1,1,1,1,1,1,1],
               [1,0,0,0,0,0,1],
               [1,0,1,1,1,0,1],
               [1,0,1,0,1,0,1],
               [1,0,1,1,1,0,1],
               [1,0,0,0,0,0,1],
               [1,1,1,1,1,1,1]]
Output: 2

 

Constraints:

• 1 <= grid.length, grid[0].length <= 100
• 0 <= grid[i][j] <=1

 

2、简要翻译：

0代表地面，1代表 水，数不与边界相连的岛屿数（上下左右 算相连）

 

3、代码思路：

广度优先搜索遍历全图，时间复杂度O（mn）

 

4、Java解题代码：

private static final int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};

    public int closedIsland(int[][] grid) {
        int m = grid.length;
        int n = grid[0].length;
        int[][] visited = new int[m][n];
        boolean flag;
        LinkedList<int[]> queue = new LinkedList<>();
        int result = 0;
        for (int i = 1; i < m - 1; i++) {
            for (int j = 1; j < n - 1; j++) {
                if (grid[i][j] == 0 && visited[i][j] == 0) {
                    flag = true;
                    queue.addLast(new int[]{i, j});
                    int[] island;
                    int I, J;
                    while (!queue.isEmpty()) {
                        island = queue.pollFirst();
                        for (int[] direction : directions) {
                            I = island[0] + direction[0];
                            J = island[1] + direction[1];
                            if (I >= 0 && I < m && J >= 0 && J < n && grid[I][J] == 0 && visited[I][J] == 0) {
                                visited[I][J] = 1;
                                queue.addLast(new int[]{I, J});
                                if (I == 0 || I == m - 1 || J == 0 || J == n - 1) {
                                    flag = false;
                                }
                            }
                        }
                    }
                    if (flag) result++;
                }
            }
        }
        return result;
    }