强化学习（Reinforcement Learning）

Created by	Created on
xbo	June 10, 2019

强化学习基本概念

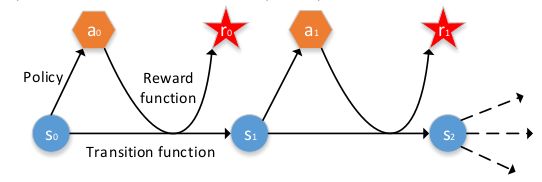
强化学习四要素：状态(state)、动作(action)、策略（policy）、奖励(reward)。

名词	解释
智能体	学习器与决策者的角色。
环境	智能体之外一切组成的、与之交互的事物。
动作	智能体的行为表征。
状态	智能体从环境获取的信息。
奖励	环境对于动作的反馈。
策略	智能体根据状态进行下一步动作的函数。
状态转移概率	智能体做出动作后进入下一状态的概率。

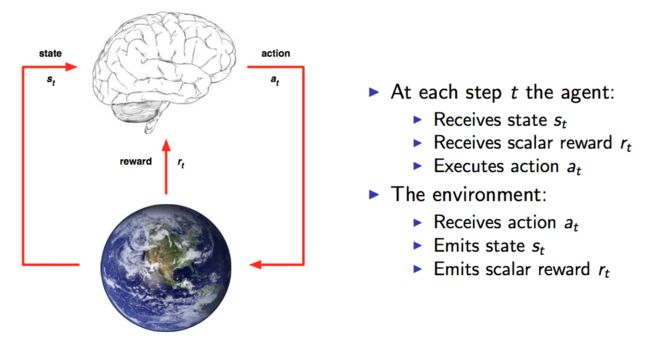
RL考虑的是智能体（Agent）与环境（Environment）的交互问题：

智能体处在一个环境中，每个状态为智能体对当前环境的感知；智能体只能通过动作来影响环境，当智能体执行一个动作后，会使得环境按某种概率转移到另一个状态；同时，环境会根据潜在的奖赏函数反馈给智能体一个奖赏。
--- 周志华《机器学习》

RL的目标是找到一个最优策略，使智能体获得尽可能多的来自环境的奖励。例如赛车游戏，游戏场景是环境，赛车是智能体，赛车的位置是状态，对赛车的操作是动作，怎样操作赛车是策略，比赛得分是奖励。在论文中中常用观察(Observation)而不是环境，因为智能体不一定能得到环境的全部信息，只能得到自身周围的信息。

强化学习基本结构

人与环境交互

在每个时间步(timestep)，智能体在当前状态根据观察来确定下一步的动作，因此状态和动作之间存在映射关系，这种关系就是策略，用表示：

记作，表示动作action，表示状态state。

学习开始时往往采用随机策略进行实验得到一系列的状态、动作和奖励样本，算法根据样本改进策略，最大化奖励。由于奖励越来越大的特性，这种算法被称作增强学习。

马尔可夫决策过程(Markov Decision Process, MDP)

马尔可夫性

系统的下一个状态仅与当前状态有关，而与历史状态无关。

此处的状态是指完全可观察的全部的环境状态

回报(Return)
为最大化长期累积奖赏，定义当前时刻后的累积奖赏为回报(Return)，考虑折扣因子(避免时间过长时，总回报无穷大)：

值函数(Value Function)
强化学习的目标是学习到一个策略来最大化期望，即希望智能体执行一系列的动作来获得尽可能多的平均回报。为评估一个策略的期望回报，需要定义值函数.

状态值函数：在状态下获得的期望回报。

状态-动作值函数：在状态下执行动作后获得的期望回报。

根据马尔可夫特性，二者有如下关系：

即状态值函数是动作-状态值函数关于动作的期望。

贝尔曼方程(Bellman equation)
$\begin{aligned} V^{\pi}(s_{t})&=E\left[R_{t} | s_{t}=s\right]=E\left[r_{t+1}+\gamma r_{t+2}+\ldots | s_{t}=s\right] \\&=E[ r_{t+1}+\gamma\left(r_{t+2}+\gamma r_{t+3}+\ldots\right) | s_{t}=s ] \\&=E\left[r_{t+1}+\gamma R_{t+1} | s_{t}=s\right] \\&=E\left[r_{t+1}+\gamma V^{\pi}\left(s_{t+1}\right) | s_{t}=s\right] \end{aligned}$

其意义在于当前状态的值函数可以通过下一状态的值函数来计算。同理，状态-动作值函数也有类似关系。

计算状态值函数的目的是为了构建学习算法从数据中得到最优策略，每个策略对应着一个状态值函数，最优策略对应着最优状态值函数。

基于值函数的学习方法

求解最优策略等价于求解最优的值函数，这是求解最优策略的一种方法，称为基于值函数的学习方法，DQN采用该算法。

最优的值必然为最大值，故等式右侧的值必然为使取最大的值。

由于值函数是对策略的评估，为不断优化直至选出最优策略，一种可行的方式是依据值函数选取策略更新的方式。常见的策略有两种：

贪婪策略

贪婪策略是一个确定性策略，即始终选取使值函数最大的策略。这是智能体对已知知识的利用(exploitation)，不好更新出更好的值，但可以得到更好的测试效果用于判断算法是否有效。
ε-greedy策略：
$\pi(a | s) \leftarrow \left\{\begin{array}{ll}{1-\varepsilon+\frac{\varepsilon}{|A(s)|}} &{\text { if } a=\underset{a}{\arg \max} Q^{\pi}(s, a)} \\ {\frac{\varepsilon}{|A(s)|}} &{\text { if } a \neq \underset{a}{\arg \max} Q^{\pi}(s, a)}\end{array}\right.$
选取不使值函数最大的动作表示智能体对未知知识的探索(exploration)，探索未知的动作会产生的未知的效果，有利于更新值，有可能获得更好的策略，故ε-greedy策略平衡了探索和利用。

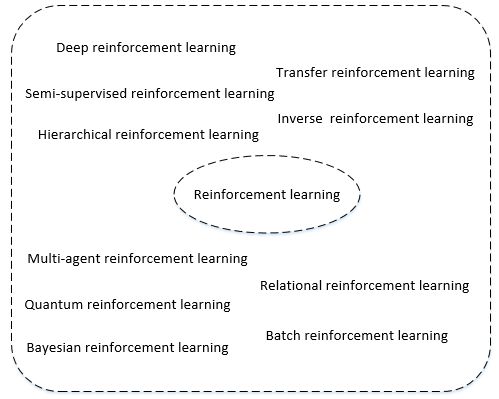
分类

马尔科夫链过程

基于模型的(Model-based)：动态规划
无模型的(Model-free)：强化学习
- 基于值函数的(Value-based)
- 基于策略梯度的(Policy-gradient)
- 基于模型的(Model-based)

DQN算法分类

强化学习分类

无模型强化学习方法

基于模型的强化学习方法(动态规划)的前提是知道环境的状态转移概率，但在实际问题中，状态转移的信息往往无法获知，由此需要数据驱动的无模型(model-free)的方法。

蒙特卡罗(Monte Carlo)方法

在无模型时，一种自然的想法是通过随机采样的经验平均来估计期望值，此即蒙特卡罗法。其过程可以总结如下：

智能体与环境交互后得到交互序列
通过序列计算出各个时刻的奖赏值
将奖赏值累积到值函数中进行更新
根据更新的值函数来更新策略

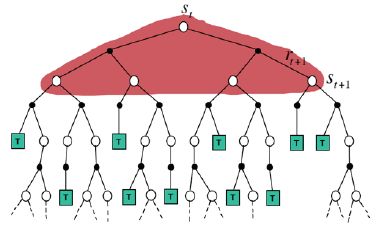
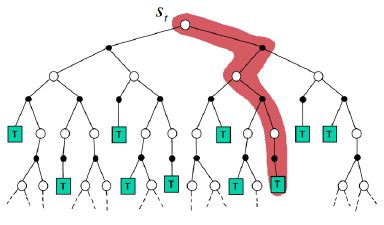
在动态规划中，为保证算法的收敛性，算法会逐个扫描状态空间中的状态，计算值函数时用到了当前状态的所有后继状态的值函数。而蒙特卡罗利用经验平均估计状态的值函数，此处的经验是指一次试验，而一次试验要等到终止状态出现才结束，因此学习速度慢，效率不高。下图较直观展示了二者的不同。

动态规划

蒙特卡罗方法

在蒙特卡罗中，如果采用确定性策略，每次试验的轨迹都是一样的，因此无法进一步改进策略。为了使更多状态-动作对参与到交互过程中，即平衡探索和利用，常用ε-greedy策略来产生动作，以保证每个状态-动作对都有机会作为初始状态，在评估状态-动作值函数时，需要对每次试验中所有状态-动作对进行估计。

时序差分方法(Temporal Difference)

由于蒙特卡罗需要获得完整轨迹，才能进行策略评估并更新，效率较低。时序差分法结合了动态规划和蒙特卡罗，即模拟一段轨迹(一步或者几步)，然后利用贝尔曼方程进行自迭代更新，如下图所示：

时序差分

对该方法的通俗理解：
你需要从A点出发，经过B点后到C点，你有两个路段（A-B,B-C)的估计用时，在一次实验中，经过A-B路段后得到一个准确用时，根据这个准确用时和B-C路段的估计用时即可得到新的全路段估计用时（即更新）。
上述例子体现了TD学习的主要原则：不必等到实验结束再沿着实验路径进行更新。

区别

蒙特卡罗使用的是值函数最原始的定义，即利用所有奖赏的累积和来估计值函数；
动态规划和时序差分则利用一步预测方法来计算当前状态值函数，不同的是，动态规划利用模型计算后继状态，时序差分利用实验得到后继状态。

Q-learning

Q学习基于时序差分得到更新Q值的方法：

迭代得到的值没有直接赋予新的Q值，而是采用递进的方式更新原有Q值，这能够减少估计误差造成的影响，类似随机梯度下降，最终收敛到最优Q值。

Q-Learning 算法

深度Q网络(Deep Q-Network, DQN)

函数近似(Function Approximation)

动态规划、蒙特卡罗、时序差分等都有一个共同前提：状态空间和动作空间是离散的且不能太大。通常值函数用表格的形式的表示(Q-Table)，故又称之为表格型强化学习。但在很多问题中，状态空间维数很大，甚至可能是连续的，无法用表格表示，即在训练过程中，仅通过反复的测试无法获得足够的样本来遍历每个状态，这样在应用过程中若遇到未遍历的状态将导致算法失败。

人类在学习过程中不可能遍历所有的情况，更多的是将新情况与记忆进行比对，如果相似，则采用相似的做法。因此，如果能用一个函数来表示值函数，输入任意的状态都能输出结果，那么就可以把Q矩阵的更新问题变成一个函数拟合问题，相近的状态也就可以得到相近的动作，这就是值函数近似（value function approximator）：，通过更新参数来使得Q函数逼近最优的Q值。

上述操作将求解值函数问题转化为函数优化问题，从而可以使用监督学习(supervised learning).监督学习是一种常见且易于解决的问题，线性回归(Linear Regression) 、支持向量机(Support Vector Machine)、决策树(Decision Tree)，以及神经网络(Neural Network )等都可以用来解决此类问题，一般做法是：

1 确定一个损失函数loss function
2 计算关于损失函数的梯度
3 使用梯度下降比如随机梯度下降(SGD)等方法来更新

使用深度神经网络做值函数近似来解决强化学习问题即是深度强化学习(Deep Reinforcement Learning,Deep Q-Learning,DQN)

DQN

DQN 结构

与Q-Learning相比，DQN主要改进在以下三个方面：
（1）DQN利用深度卷积网络(Convolutional Neural Networks,CNN)来逼近值函数；
（2）DQN利用经验回放训练强化学习的学习过程；

Q-Leaning 方法基于当前策略进行交互和改进，每一次模型利用交互生成的数据进行学习，学习后的样本被直接丢弃。但如果使用机器学习模型代替表格式模型后再采用这样的在线学习方法，就有可能遇到两个问题，这两个问题也都和机器学习有关。

交互得到的序列存在一定的相关性。交互序列中的状态行动存在着一定的相关性，而对于基于最大似然法的机器学习模型来说，我们有一个很重要的假设：训练样本是独立且来自相同分布的，一旦这个假设不成立，模型的效果就会大打折扣。而上面提到的相关性恰好打破了独立同分布的假设，那么学习得到的值函数模型可能存在很大的波动。
为解决以上两个问题，引入经验回放。Replay Buffer 包含了收集样本和采样样本两个过程。收集的样本按照时间先后顺序存入结构中，如果Replay Buffer 已经存满样本，那么新的样本会将时间上最久远的样本覆盖。而对采样来说，如果每次都取出最新的样本，那么算法就和在线学习相差不多；一般来说，Replay Buffer 会从缓存中均匀地随机采样一批样本进行学习。这样，每次训练的样本通常来自多次交互序列，这样单一序列的波动就被减轻很多，训练效果也就更加稳定。同时，一份样本也可以被多次训练，提高了样本的利用率。

交互数据的使用效率。采用梯度下降法进行模型更新时，模型训练往往需要经过多轮迭代才能收敛。每一次迭代都需要使用一定数量的样本计算梯度，如果每次计算的样本在计算一次梯度后就被丢弃，那么我们就需要花费更多的时间与环境交互并收集样本。

为解决以上两个问题，引入经验回放。Replay Buffer 包含了收集样本和采样样本两个过程。收集的样本按照时间先后顺序存入结构中，如果Replay Buffer 已经存满样本，那么新的样本会将时间上最久远的样本覆盖。而对采样来说，如果每次都取出最新的样本，那么算法就和在线学习相差不多；一般来说，Replay Buffer 会从缓存中均匀地随机采样一批样本进行学习。这样，每次训练的样本通常来自多次交互序列，这样单一序列的波动就被减轻很多，训练效果也就更加稳定。同时，一份样本也可以被多次训练，提高了样本的利用率。

（3）DQN独立设置了目标网络来单独处理时序差分中的偏差。

在Q-Learning中，通过当前时刻的回报和下一时刻的价值估计进行更新，由于数据本身存在着不稳定性，每一轮迭代都可能产生一些波动，这些波动会立刻反映到下一个迭代的计算中，这样我们就很难得到一个平稳的模型。为了减轻相关问题带来的影响，需要尽可能地将两个部分解耦，由此引入目标网络，其训练过程如下：

在训练开始时，两个模型使用完全相同的参数。

在训练过程中， Behavior Network 负责与环境交互，得到交互样本。

在学习过程中，由Q-Learning 得到的目标价值由Target Network 计算得到；然后用它和Behavior Network 的估计值进行比较得出目标值并更新Behavior Network。

每当训练完成一定轮数的迭代， Behavior Network 模型的参数就会同步给Target Network ，这样就可以进行下一个阶段的学习。

通过使用Target Network ，计算目标价值的模型在一段时间内将被固定，这样模型可以减轻模型的波动性。

DQN完整算法

DQN完整算法

具体训练过程：

Step 1: 用一个深度神经网络来作为值的值函数近似，参数为：

Step 2: 在值中使用均方差来定义目标函数即损失函数：

此处Target即为算法流程中的目标网络。

Step 3：计算参数关于损失函数的梯度：

Step 4: 使用SGD实现End-to-end的优化目标
得到上述梯度，且可以从深度神经网络中进行计算，因此可以使用随机梯度下降算法来更新参数，从而得到最优的Q值。

强化学习基础知识详解