【原】对频率论（Frequentist）方法和贝叶斯方法（Bayesian Methods）的一个总结

注：

本文是对《IPython Interactive Computing and Visualization Cookbook》一书中第七章【Introduction to statistical data analysis in Python – frequentist and Bayesian methods】的简单翻译和整理，这部分内容主要将对统计学习中的频率论方法和贝叶斯统计方法进行介绍。

 

本文将介绍如何洞察现实世界的数据，以及如何在存在不确定性的情况下做出明智的决定。

统计数据分析的目的是通过一部分不确定的观测现象了解一个复杂的，真实世界。数据的不确定性导致了我们获得的关于现象知识的不确定。该理论的一个主要目标是量化这种不确定性。

 

一、常见词汇表

统计推理（Statistic inference）包括通过部分的不确定的观察数据获取一个关于未知过程的信息。特别是，估计（Estimation）承担着获取用于描述该过程的数学变量的大致度量。

决策理论（Decision theory）使我们能够通过随机的观测样本，以一个能够控制的风险，对一个未知过程进行决策。

 

二、频率论和贝叶斯方法

         对于不确定性的度量至少有两种不同的考虑方式，这导致了两种不同类型的推理/决策方法/其他统计问题，我们称之为频率论（frequentist）和贝叶斯方法(Bayesian methods)。

         频率论方法通过大量独立实验将概率解释为统计均值（大数定律） ；贝叶斯方法则将概率解释为信念度（degree of belief）（不需要大量的实验） 。当考虑的试验次数非常少的时候，贝叶斯方法的解释非常有用。此外，贝叶斯理论将我们对于随机过程的先验知识纳入考虑，当我们获得的数据越来越多的时候，这个先验的概率分布就会被更新到后验分布中。

         频率论和贝叶斯方法都各有其优劣的地方。例如，频率论方法比贝叶斯方法更容易实施，然而却更难解释。对于频率论应用的典型错误可以参看：《Statistics Done Wrong》。

 

三、参数推理方法 vs 非参数推理方法

         在许多情况下，我们的分析是基于概率模型，这个模型描述了数据是如何产生的。概率模型没有实体（reality），它仅仅是一个用来指导分析的数学对象。一个好的模型可能非常有用，而一个不好的模型可能会误导你。

         使用参数推理方法，可以认为模型属于已知的某个概率分布簇（family of probability distributions），该模型有一个或多个有待估计的数值参数。

         使用非参数推理方法，在模型中不需要进行这样的假设，这使得模型的建立非常灵活。然而这种方法通常在实施和解释的时候会更加复杂。

 

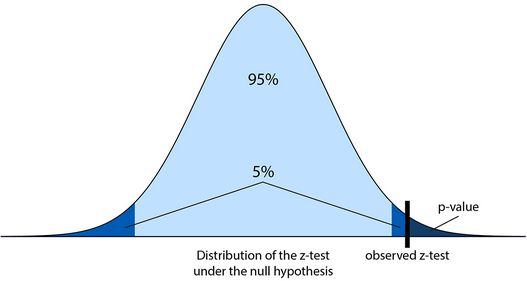
四、使用简单的z-test开始假设检验（频率论方法）

         统计假设检验允许我们在数据不完整的情况下做出决策，当然从定义上说，这些决策是不确定的。统计学家已经制定了严格的方法来评估这种风险。然而，在进行决策的过程中总会涉及一些主观性。理论只是在不确定的世界中帮助我们进行决策的一种工具。

 

在进行假设检验时许多频率论的方法大致上包含以下步骤：

1、  写出假设，尤其是零假设（Null hypothesis），它与我们要（以一定的置信度）证明的假设相反。

2、  计算检验统计量，这是一个数学公式，取决于检验的类型，模型，假设和数据。

3、  使用计算出的值接受假设，或者拒绝假设，或者未能得出结论。

 

我们将一枚硬币抛掷次，观察到正面的次数是次。我们想知道这枚硬币是否是公平的（零假设）。这个例子非常简单但是对于教学来说相当不错，此外，它还是许多复杂方法的基础。

我们使用表示伯努利分布，其中是未知参数。伯努利变量定义为：

l  为0（硬币是反面）的概率是

l  为1（硬币是正面）的概率是

下面是进行简单的统计Z检验所需的步骤：

1、            我们假设经过次投掷硬币后，出现正面的次数是。我们选择显著性水平为0.05，这枚硬币是否公平？我们的零假设是：这枚硬币是公平的（）。

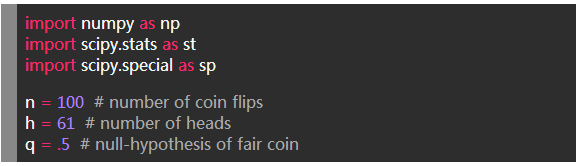
2、            我们开始计算z-score，它是由下面的公式定义的（xbar是对分布平均的估计）：

3、            现在通过z-score，我们可以用下面的方式计算：

4、            这个比0.05小，因此我们拒绝零假设并且得出结论：这枚硬币可能是不公平的。

 

工作原理

         这个抛掷硬币的实验被模拟成个独立同分布的随机变量，它们都服从伯努利分布。每个代表一次硬币抛掷。实验结束后，我们从这些变量中得到了真实的值（样本）。一个不同的概念通常用来区分随机变量（概率对象）和实际的值（样本）。

         下面的公式给出了样本均值的定义（这里是硬币正面出现的比例）：

                                                                               

已知伯努利分布的期望和方差，我们来计算：

                                                                            

                                                                   

z检验（z-test）是对进行的标准化（减去均值，除以它的标准差，使得形成的变量均值为0，标准差为1）。

                                                         

         根据零假设，获取的z-test比指定的高的概率是什么？这个概率就被称作是（双侧）。根据中心极限定理（Central Limit Theorem），对于比较大的来说，z-test近似的服从一个标准正态分布，因此我们可以得到：

                                               

         下面的一幅图对z-score和进行了说明：

在上面的公式中，是标准正态分布的累计分布函数（cumulative distribution function）。在SciPy中，可以通过scipy.stats.norm.cdf来计算它。因此，给定一个从数据中计算得到的z-test值，我们就可以通过该函数来计算其。在零假设下，观察到z-test的概率应该远远大于给定的置信度。

         如果比5%（在实验开始时选择的显著性水平）小，我们可以得出结论：

l  零假设是不正确的，也就是说硬币是不公平的；

l  或者零假设是正确的，得到这样的是由于运气太差了，因此我们不能得出结论。 

在这种框架下我们无法消除这两种选择的歧义，但通常情况下都会选择第一种结论。这是这种方法的一个缺陷，虽然也可以使用一些其他的方法来解决这个问题（例如，我们可以分别独立进行多次不同实验来观察它们的结果）。 

         许多统计检验都使用上述这个模式来检验数据中存在的各种特性，《Statistical hypothesis testing》中给出了一些常见的统计假设检验。

         由于解释起来并不容易，即使在同行评审（peer-reviewed）的科学出版物中，仍然可能会出现错误的结论。 《Statistics Done Wrong》中给出了关于该问题的一些深入话题。

五、使用贝叶斯方法

         上一节中，我们使用了频率论的方法来对不完整的数据进行假设检验。本节中，我们将介绍另一种基于贝叶斯理论的方法。其主要思想是将未知参数当作是随机变量，就像描述试验时使用的变量一样。关于参数的先验知识被集成到模型中，随着观察到的数据越来越多，这些知识会被一直更新。

         频率论方法和贝叶斯方法对于概率的解释不太一样。频率论认为概率是当样本的数量趋近于无穷时（样本出现）频率的极限。贝叶斯方法将其解释为一种信念（belief），它将会随着观测数据的增加而不断被更新。

         这里，我们将使用贝叶斯方法重新进行之前的硬币抛掷实验

 

具体做法：

         我们将定义为观察到硬币正面的概率。在上一节中只是一个固定的数字，然而此处我们将其看作是一个随机变量。最初，这个变量遵循一种称之为先验分布（prior distribution）的分布，它代表了在开始进行抛掷硬币之前我们对于的知识。我们将会在每次试验之后更新这个分布（后验分布，posterior distribution）。

 

1、  首先，我们假设是一个在[0,1]上服从均匀分布的随机变量。这就是我们的先验分布：对于所有的来说，。

2、  然后，我们开始抛掷次硬币，将定义为第次抛掷硬币试验的结果（反面是0，正面是1）。

3、  当观测到后的概率分布变为什么？贝叶斯公式使我们可以计算后验概率分布：

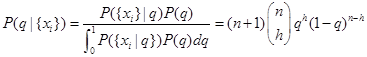
4、  我们在Python中根据上述数学公式定义后验分布，我们将这个式子定义为二项分布的概率论密度函数（Probability Mass Function, pmf）的倍：

5、  在观测到次正面和总次数时我们对这个分布的图像进行绘制：

 

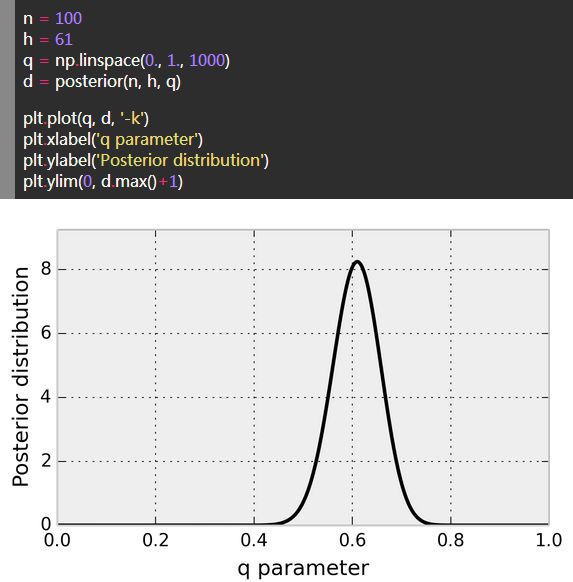
这条曲线代表了在观测到61次正面后，对于参数的信念。

 

工作原理：

在这节中我们将会解释贝叶斯定理，然后解释这个例子背后的数学细节。

 

贝叶斯定理：

使用一个数学模型来对数据进行解释是数据科学中非常通用的一个想法，这被定义为一个单向的过程：。一旦这个模型被确定，数据科学家的任务就变为利用数据恢复关于该模型的信息。换句话说，我们想对原始的过程进行反转：。

         在一个概率集合中，上述正向的过程被表示为一个条件概率，这是模型被完全指定后观测数据出现的概率。与此相同的，反向的过程也可以表示为一个条件概率，这在得到观测数据（我们进行试验后可以得到的数据）后提供了关于（我们正在寻找的）模型的信息。

         贝叶斯定理是对概率过程进行反转的通用框架的核心。它可以被定义为：

                                             

当我们得到了观测数据后，这个公式提供了关于模型的信息。贝叶斯公式被广泛的应用于信号处理，统计，机器学习，反向问题（inverse problems）和许多其他的科学应用。

        

在贝叶斯公式中，反映了我们对于模型的先验知识。是数据的分布，它通常被描述为对的积分。

总之来说，贝叶斯公式为我们提供了一个关于数据推断的通用路线图：

1、  为正向过程（数据推理过程）指定一个数学模型（）；

2、  为模型指定先验知识（）；

3、  为求解公式进行分析或者数值运算；

 

计算后验分布

在这个例子中，我们可以通过贝叶斯定理得到后验分布服从下面的公式：

                                                        

由于是相互独立的，因此我们可以得到（是正面向上的次数）：

                                             

此外，我们可以分析计算如下积分（使用分部积分推导）：

                                     

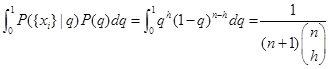
最终，我们将得到：

                                 

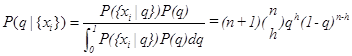
对后验概率进行最大估计

         我们可以从后验分布中进行点估计。例如，对于这个分布中的q作最大后验估计（maximum a posteriori(MAP) estimation）。

         这里我们可以通过对后验概率中的求导进行估计，假定可以得到：

                   

当时，该表达式等于0，这就是对于参数的最大后验估计。在这个例子中，这个值恰好是实验中正面向上出现的比例。