《SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS》论文阅读（二）

GCN的定义

下面内容参考kipf博客，个人认为是告诉你从直觉上，我们怎么得到GCN图上的定义（而前面的大幅推导是从理论上一步一步来的，也就是说可以用来佐证我们的直觉）

我们的网络输入是\(\mathcal{G}=(\mathcal{V},\mathcal{E})\)：

• 即可以用\(N\times D\)的矩阵\(X\)表示，\(N\)为图上结点个数，\(D\)是每个结点的特征维数
• 同时表示一个图还需要邻接矩阵\(A\)

而一层的输出记作\(Z_{\mathbb{R}^{N \times F}}\)，其中\(N\)还是结点个数，\(F\)为每个结点的特征维数

那么非线性神经网络就可以定义成如下形式：

\[H^{l+1}=f(H^{l}, A) \]

其中\(H^{0}=X\), \(H^{L}=Z\), \(L\) 表示网络的层数，那么模型的关键是如何设计\(f(\cdot )\)

一种简单的形式

\[f(H^{l}, A) = \sigma (AH^{l}W^{l}) \]

其中\(W^{l}\) 是\(l.th\)层的参数矩阵，\(\sigma ()\) 是激活函数。【PS:Despite its simplicity this model is already quite powerful】
仔细观察上式就能发现几个缺陷：

• 其中\(A\)是邻接矩阵，对角线上为\(0\)，导致经过网络中的一层，没有加上自己本结点的信息，所以改造替换成 \(\hat{A} = A+I\)
• 可是\(\hat {A}H\) 则是自己+相邻结点特征总和，还需平均化，所以改成 \(D^{-1}\hat {A}H\)
• 我们还可以更进一步，考虑到上篇说的拉普拉斯算子计算中周围结点总和\(-\)中心点*相邻结点个数，即相当于每个相邻点能量\(-\)中心点能量。类比过来，相邻点给我影响是:(相邻点能量/相邻点本身邻居个数)，所以有\(D^{-1/2}\hat{A}D^{-1/2}\)

\[f(H^{(l+1)}, A) = \sigma\left( D^{-\frac{1}{2}}\hat{A}D^{-\frac{1}{2}}H^{(l)}W^{(l)}\right) \, \]

这个形式已经和上篇利用谱理论推导处理的结果很相近了

\[\boldsymbol{g}_{\boldsymbol{\theta^{\prime}}} * \boldsymbol{x} = \theta(\boldsymbol{I_n} + \boldsymbol{D}^{-1/2} \boldsymbol{W} \boldsymbol{D}^{-1/2}) \boldsymbol{x} \]

但和最终的结果还不一样，回顾论文给的 renormalization trick：

\[I_{N}+D^{-1/2}AD^{-1/2}=D^{-1/2}\hat{A}D^{-1/2}\rightarrow \tilde{D}^{-1/2}\hat{A}\tilde{D}^{-1/2}=(D+I_{N})^{-1/2}\hat{A}(D+I_{N})^{-1/2} \]

\[\hat{A}=A+I_{N} \]

\[\tilde{D}_{ii}= \sum_{}^{j}\hat{A}_{ij}=D+I_{N} \]

那么的确可以得到最终形式：

\[f(H^{(l+1)}, A) = \sigma\left(\tilde{D}^{-\frac{1}{2}}\hat{A}\tilde{D}^{-\frac{1}{2}}H^{(l)}W^{(l)}\right) \, \]

WEISFEILER-LEHMAN算法

作者试图使用Weifeiler-Lehman算法来解释GCN的表征能力。\(WL\)算法是用来判断两个graph是否同构（简单说是两图拓扑结构相同）的，WL算法

算法包含两个关键点

• 聚合自己和邻接结点信息，若记\(h\_aggregate^{t}_{i}\)，\(t\)是第几次迭代，\(i\) 是第几个结点
• 利用hash函数吐出唯一的值，\(h^{t+1}_{i}=hash(h\_aggregate^{t}_{i})\) 代替\(i\) 结点的特征

然后循环迭代

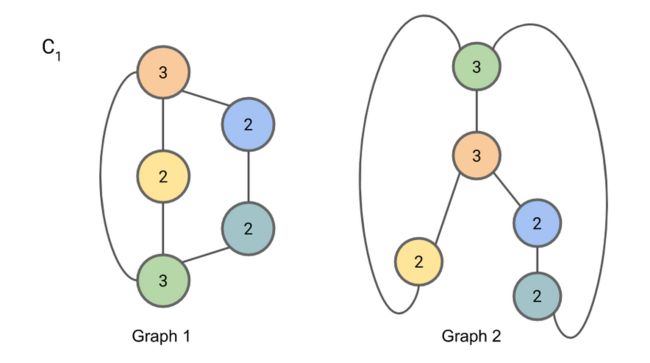
下面一个简单小例子（默认各个结点信息是相同的，所以序号均标为1，主要判断拓扑结构是否同构）：

进行信息聚合，因为默认结点是一致的，所以主要通过邻接关系判断是否同构，\(\{1,1,1\}\)即是该结点的相邻结点是谁

输入hash()函数，并且代替原有结点信息

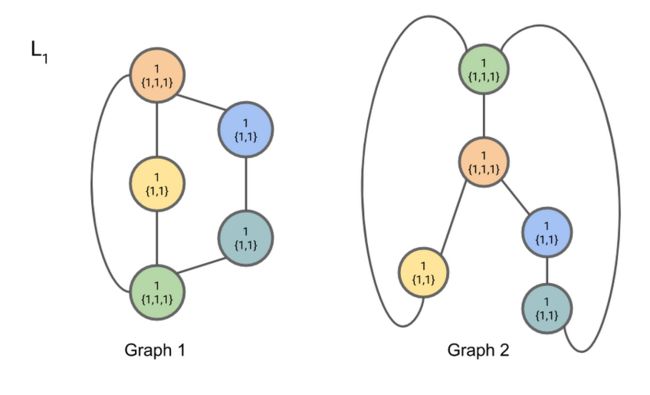
重复上述操作（具体参见：https://www.davidbieber.com/post/2019-05-10-weisfeiler-lehman-isomorphism-test/#）
最后结果：

通过判断 \(9,8,7\) 两个图个数相同，判断是同构

WEISFEILER-LEHMAN算法反映什么

\(WL\)算法由于\(hash()\)函数的使用，使得通过不断迭代，能够表征不能不同结点的差异——即结点自身信息+结点的邻居所带来的差异

代替WL的hash()函数

\[h^{l+1}_{i}=\sigma (\sum_{j\in \mathcal{N_{i}}}^{}\frac{1}{c_{ij}}h_{j}^{l}W^{l}) \]

\(N_{i}\)是结点\(j\)的相邻结点，上式可进一步化成矩阵形式

\[h^{l+1}_{i}=\sigma (D^{-1/2}AD^{-1/2}h_{j}^{l}W^{l}) \]

通过调整\(W^{l}\)参数，实现\(hash()\)的功能。也就是说这种形式的GCN对结点的表征能力可以达到hash()函数级别，作者借此来证明GCN的能力。
可是有个疑问吧，这里用的是\(D^{-1/2}AD^{-1/2}\)，其实和上文提到的\(\tilde{D}^{-1/2}\hat{A}\tilde{D}^{-1/2}\)，也还是有区别的，前者不是GCN的最终形式。。。。

参考

https://www.zhihu.com/question/54504471

http://tkipf.github.io/graph-convolutional-networks/

https://www.davidbieber.com/post/2019-05-10-weisfeiler-lehman-isomorphism-test/#

https://arxiv.org/abs/1609.02907