- 【LlamaIndex核心组件指南 | 模型篇】一文通晓 LlamaIndex 模型层:LLM、Embedding 及多模态应用全景解析
Langchain系列文章目录01-玩转LangChain:从模型调用到Prompt模板与输出解析的完整指南02-玩转LangChainMemory模块:四种记忆类型详解及应用场景全覆盖03-全面掌握LangChain:从核心链条构建到动态任务分配的实战指南04-玩转LangChain:从文档加载到高效问答系统构建的全程实战05-玩转LangChain:深度评估问答系统的三种高效方法(示例生成、手
- 2025-6-28-C++ 学习 模拟与高精度(8)
文章目录2025-6-28-C++学习模拟与高精度(8)P1591阶乘数码题目描述输入格式输出格式输入输出样例#1输入#1输出#1提交代码P1249最大乘积题目描述输入格式输出格式输入输出样例#1输入#1输出#1提交代码P1045[NOIP2003普及组]麦森数题目描述输入格式输出格式输入输出样例#1输入#1输出#1说明/提示提交代码2025-6-28-C++学习模拟与高精度(8) 模拟题,Co
- 用 Python 开发文字冒险游戏:从零开始的教程
晓天天天向上
pythonmicrosoft开发语言
文字冒险游戏(Text-basedAdventureGame)是一种经典的游戏类型,玩家通过输入文字指令与游戏世界互动。这种游戏不依赖复杂的图形界面,非常适合初学者学习编程逻辑和用户交互。在本篇博客中,我们将用Python开发一个简单的文字冒险游戏,体验游戏开发的乐趣。1.游戏设计思路游戏背景玩家醒来发现自己身处一个神秘的地下城,需要探索房间、收集物品、战胜敌人并找到出口。核心机制房间导航:玩家可
- 从零开始理解零样本学习:AI人工智能必学技术
AI天才研究院
AgenticAI实战AI人工智能与大数据AI大模型企业级应用开发实战ai
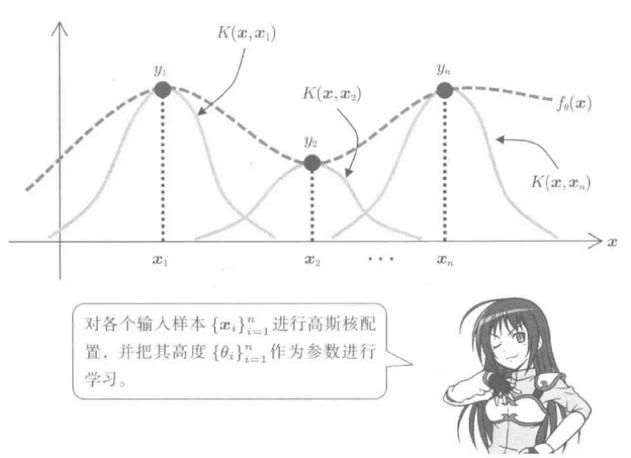
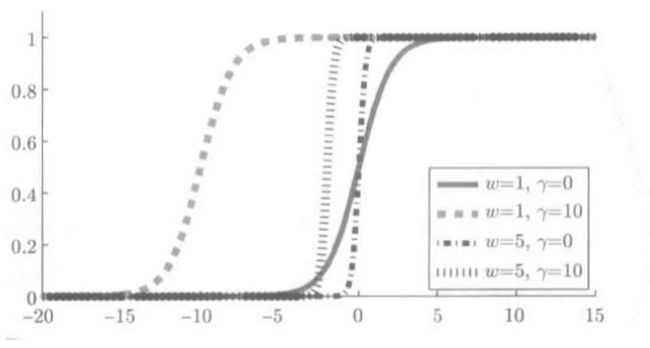
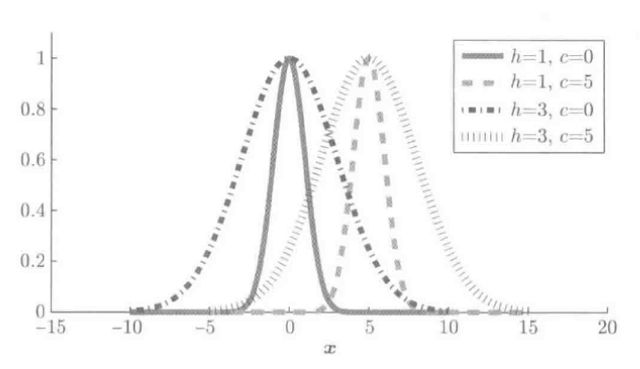
从零开始理解零样本学习:AI人工智能必学技术关键词:零样本学习、人工智能、机器学习、知识迁移、语义嵌入摘要:本文旨在全面深入地介绍零样本学习这一在人工智能领域具有重要意义的技术。首先阐述零样本学习的背景和基本概念,通过详细的解释和直观的示意图让读者建立起对零样本学习的初步认识。接着深入剖析其核心算法原理,结合Python代码进行详细说明,同时引入相关数学模型和公式并举例阐释。通过项目实战部分,带领
- 2025 VUE常见面试题
hmildj
vue.js面试前端
前言总结一些VUE面试的基础知识,共同学习1.什么是Vue?答案:Vue.js(通常简称为Vue)是一个用于构建用户界面的渐进式JavaScript框架,Vue3是Vue.js框架的最新版本,它引入了许多改进和优化,包括性能提升、更好的类型支持、组合API等。2.MVVM模式是什么?Vue如何体现这一模式?答案:MVVM将视图(View)与数据(Model)通过ViewModel层解耦,Vue
- 初学翁凯老师的c语言后对其中一些问题的看法
Obltv
#初学c语言c语言
文章目录初学翁凯老师的c语言后对其中一些问题的看法一、一个课后的简单逻辑语法问题二、解答和一些思考1.**++i++--**2.**i++++**3.**a=b+=c++-d+--e/-f**问题初探原代码逻辑举例初次写博客的看法及感受初学翁凯老师的c语言后对其中一些问题的看法学习c语言已有数天,其中一些问题今日来看仍有研究价值,故记录探讨之一、一个课后的简单逻辑语法问题++i+±-i++++a=
- 高斯混合模型(Gaussian Mixture Model, GMM)
不想秃头的程序
神经网络语音识别人工智能深度学习网络
高斯混合模型(GaussianMixtureModel,GMM)是一种概率模型,用于表示数据点由多个高斯分布(GaussianDistribution)混合生成的过程。它广泛应用于聚类分析、密度估计、图像分割、语音识别等领域,尤其适合处理非球形簇或多模态数据。以下是GMM的详细介绍:一、核心思想GMM假设数据是由多个高斯分布混合生成的,每个高斯分布代表一个簇(Cluster),并引入隐变量(Lat
- 卷积神经网络(Convolutional Neural Network, CNN)
不想秃头的程序
神经网络语音识别人工智能深度学习网络卷积神经网络
卷积神经网络(ConvolutionalNeuralNetwork,CNN)是一种专门用于处理图像、视频等网格数据的深度学习模型。它通过卷积层自动提取数据的特征,并利用空间共享权重和池化层减少参数量和计算复杂度,成为计算机视觉领域的核心技术。以下是CNN的详细介绍:一、核心思想CNN的核心目标是从图像中自动学习层次化特征,并通过空间共享权重和平移不变性减少参数量和计算成本。其关键组件包括:卷积层(
- ResNet(Residual Network)
不想秃头的程序
神经网络语音识别人工智能深度学习网络残差网络神经网络
ResNet(ResidualNetwork)是深度学习中一种经典的卷积神经网络(CNN)架构,由微软研究院的KaimingHe等人在2015年提出。它通过引入残差连接(SkipConnection)解决了深度神经网络中的梯度消失问题,使得网络可以训练极深的模型(如上百层),并在图像分类、目标检测、语义分割等任务中取得了突破性成果。以下是ResNet的详细介绍:一、核心思想ResNet的核心创新是
- 平台再升级!接入DeepSeek AI,三大能力一键生成
橙武科技
低代码AIdeepseek人工智能
在数字化项目落地过程中,很多企业都会面临相同的问题:数据库建模要写SQL表结构;业务流程需要画LogicFlow流程图;前端页面还要写AMISJSON配置。从想法到实现,中间至少要经历产品经理、架构师、后端、前端多轮沟通。每个环节都耗时,改起来还要推翻重来。demo地址:https://admin.cwcode.top✨我们的平台,现在直接整合了DeepSeekAI大模型只要输入一句需求,就能:✅
- P25:LSTM实现糖尿病探索与预测
?Agony
lstm人工智能rnn
本文为365天深度学习训练营中的学习记录博客原作者:K同学啊一、相关技术1.LSTM基本概念LSTM(长短期记忆网络)是RNN(循环神经网络)的一种变体,它通过引入特殊的结构来解决传统RNN中的梯度消失和梯度爆炸问题,特别适合处理序列数据。结构组成:遗忘门:决定丢弃哪些信息,通过sigmoid函数输出0-1之间的值,表示保留或遗忘的程度。输入门:决定更新哪些信息,同样通过sigmoid函数控制更新
- Python训练营打卡——DAY16(2025.5.5)
cosine2025
Python训练营打卡python开发语言机器学习
目录一、NumPy数组基础笔记1.理解数组的维度(Dimensions)2.NumPy数组与深度学习Tensor的关系3.一维数组(1DArray)4.二维数组(2DArray)5.数组的创建5.1数组的简单创建5.2数组的随机化创建5.3数组的遍历5.4数组的运算6.数组的索引6.1一维数组索引6.2二维数组索引6.3三维数组索引二、SHAP值的深入理解三、总结1.NumPy数组基础总结2.SH
- 【重构推荐系统】国产大模型驱动的电商个性化推荐完整实战:架构设计、推理优化与在线部署闭环
观熵
国产大模型部署实战全流程指南重构人工智能Agent智能体落地方案
个人简介作者简介:全栈研发,具备端到端系统落地能力,专注大模型的压缩部署、多模态理解与Agent架构设计。热爱“结构”与“秩序”,相信复杂系统背后总有简洁可控的可能。我叫观熵。不是在控熵,就是在观测熵的流动个人主页:观熵个人邮箱:
[email protected]座右铭:愿科技之光,不止照亮智能,也照亮人心!专栏导航观熵系列专栏导航:AI前沿探索:从大模型进化、多模态交互、AIGC内容生成,到
- 深入详解:决策树算法的概念、原理、实现与应用场景
猿享天开
算法决策树机器学习
深入详解:决策树算法的概念、原理、实现与应用场景决策树(DecisionTree)是机器学习中一种直观且广泛应用的监督学习算法,适用于分类和回归任务。其树形结构易于理解,特别适合初学者。本文将从概念、原理、实现到应用场景,全面讲解决策树,并通过流程图和可视化示例增强理解,通俗易懂,帮助小白快速掌握决策树算法相关知识。1.决策树的概念1.1什么是决策树?决策树通过一系列条件判断(决策节点)将输入数据
- [学习] PID算法原理与实践(代码示例)
极客不孤独
学习算法c语言
PID算法原理与实践文章目录PID算法原理与实践一、PID算法原理1.1PID算法概述1.定义2.应用领域3.核心目标1.2基本原理1.3数学表达离散化实现(适用于数字控制)二、实践案例(C语言)1.电机转速控制2.温度控制系统3.时钟驯服系统三、常见问题与优化1.积分饱和(Windup)问题2.噪声干扰问题3.非线性系统适配问题四、扩展方向1.数字PID与模拟PID的差异2.变参数PID(如增益
- [学习] C语言编程中线程安全的实现方法(示例)
极客不孤独
学习c语言安全
C语言编程中线程安全的实现方法在多线程编程中,线程安全(ThreadSafety)是一个非常重要的概念。当多个线程同时访问共享资源时,如果没有合理的同步机制,就可能导致数据竞争、死锁甚至程序崩溃。本文将详细介绍在C语言中如何实现线程安全的几种主要方式,并提供可以实际运行的代码示例。文章目录C语言编程中线程安全的实现方法一、什么是线程安全?二、C语言中线程安全的实现方式方法一:互斥锁(Mutex)✅
- ✨【Blender/Houdini 渲染必看】CPUⓥⓢGPU?3 分钟选对算力不踩坑!
渲染101专业云渲染
blenderhoudini分布式服务器maya
核心问题速答Q:渲染该选CPU还是GPU?✅CPU:复杂场景/批量渲染/预算可控首选✅GPU:单帧速度/实时预览/急单交付必选维度1:硬件硬刚——CPU凭啥赢麻了?▫️多线程王者:16核/32核服务器矩阵,支持50-300台并行渲染▫️场景兼容性:粒子特效/全局光照/超复杂模型稳定输出秘密武器:CPU批量渲染100帧耗时=GPU单帧耗时,整体效率持平!⚙️维度2:动态计费逻辑——成本由什么决定?计
- Golang Fiber框架最佳实践:如何构建企业级应用
Golang编程笔记
Golang编程笔记Golang开发实战golang开发语言后端ai
GolangFiber框架最佳实践:如何构建企业级应用关键词:Golang、Fiber框架、企业级应用、最佳实践、Web开发摘要:本文聚焦于GolangFiber框架在企业级应用构建中的最佳实践。详细介绍了Fiber框架的背景、核心概念、算法原理、数学模型等基础知识,通过具体的代码案例展示了如何搭建开发环境、实现和解读源代码。同时探讨了Fiber框架在实际应用场景中的应用,推荐了相关的学习资源、开
- 代码随想录算法训练营第52天| 101. 孤岛的总面积、102. 沉没孤岛、103. 水流问题、104.建造最大岛屿
扛过今天777
算法深度优先
101.孤岛的总面积卡码题目链接:101.孤岛的总面积学习链接:代码随想录题解:法一:count=0defdfs(grid,x,y):globalcountgrid[x][y]=0count+=1directions=[[1,0],[0,1],[-1,0],[0,-1]]fori,jindirections:next_x=x+inext_y=y+jifnext_x=len(grid)ornext_
- PillarNet: Real-Time and High-PerformancePillar-based 3D Object Detection
justtoomuchforyou
目标检测人工智能计算机视觉智驾
ECCV2022paper:[2205.07403]PillarNet:Real-TimeandHigh-PerformancePillar-based3DObjectDetectioncode:https://github.com/VISION-SJTU/PillarNet-LTS纯点云基于pillar3D检测模型网络比较SECOND基于voxel,one-stage,基于sparse3Dc
- 深入研究 Golang 领域的 Fiber 框架架构
Golang编程笔记
golang架构网络ai
深入研究Golang领域的Fiber框架架构关键词:Golang、Fiber框架、架构、高性能、Web开发摘要:本文将深入探讨Golang领域的Fiber框架架构。我们会先介绍背景知识,包括目的、预期读者等。接着用通俗易懂的方式解释核心概念,如Fiber框架的各个组成部分,以及它们之间的关系。然后详细阐述核心算法原理、数学模型,通过实际代码案例展示其应用。还会介绍Fiber框架的实际应用场景、推荐
- Prompt Engineering for Large Language Models
三月七꧁ ꧂
论文合集llm+promptprompt语言模型人工智能自然语言处理pdfjavascript前端
题目大型语言模型的快速工程简介 随着OpenAI的ChatGPT和Google的Bard等软件的普及,大语言模型(LLM)已经渗透到生活和工作的许多方面。例如,ChatGPT可用于提供定制食谱,建议替换缺失的成分。它可用于起草研究提案、用多种编程语言编写工作代码、在语言之间翻译文本、协助政策制定等等(Gao2023)。用户通过“提示”或自然语言指令与大型语言模型进行交互。精心设计的提示可以带
- RAG应用的评估(一)
AI老炮
AIGCai机器学习人工智能语言模型
前言上篇文档主要是对Advanced-RAG的定义、策略和适用场景做了一个细致的分析,那么当我们准备将一个基于大模型的RAG应用投入生产时,如何去判断这个RAG是否合理呢?下面有一些问题是需要提前考并应付的:LLM输出的不确定性会带来一定的不可预知性。一个RAG应用在投入生产之前需要科学的测试以衡量这种不可预知性。在LLM应用上线后的持续维护中,需要科学、快速、可复用的手段来衡量其改进效果,比如回
- 算法竞赛备考冲刺必刷题(C++) | 洛谷 P8814 解密
热爱编程的通信人
算法c++开发语言
本文分享的必刷题目是从蓝桥云课、洛谷、AcWing等知名刷题平台精心挑选而来,并结合各平台提供的算法标签和难度等级进行了系统分类。题目涵盖了从基础到进阶的多种算法和数据结构,旨在为不同阶段的编程学习者提供一条清晰、平稳的学习提升路径。欢迎大家订阅我的专栏:算法题解:C++与Python实现!附上汇总贴:算法竞赛备考冲刺必刷题(C++)|汇总【题目来源】洛谷:P8814[CSP-J2022]解密-洛
- MCP-Proxy:开发多LLM & 多MCP 支持并安全访问MCP Server的秘密
IT古董
技术杂谈安全MCPMCP-Proxy
在构建多模型、多协议、可控可信的大模型接入平台时,MCP-Proxy扮演着关键中枢。它不仅要支持多个LLM接入,还要保障对后端MCPServer的安全访问、请求审计、能力切换与资源隔离。什么是MCP/MCP-Proxy?MCP(ModelCapabilityProtocol)是新一代模型能力调用协议,类似于OpenAI的API,但可支持:多厂商大模型(OpenAI、DeepSeek、Yi、Chat
- Linux I/O 文件操作详解:从系统调用到实际工程应用
平凡灵感码头
linux学习linux运维服务器
一、写在前面在Linux或任何类Unix操作系统中,文件是一切的核心——无论是硬盘上的文本文件,还是串口设备、GPIO寄存器、甚至网络接口,几乎都被抽象为“文件”。理解Linux下的I/O文件操作机制,不仅是嵌入式开发的基础,也是进行系统编程与底层控制的关键。二、I/O的本质:一切皆文件Linux将外设抽象成文件的方式,统一了对各种资源的操作模型。你可以用open打开串口设备/dev/ttyS0,
- Spring AI快速入门
学java的cc
spring大数据java
一、引入依赖org.springframework.aispring-ai-starter-model-openaiorg.springframework.aispring-ai-bom${spring-ai.version}pomimport二、配置模型spring:ai:openai:base-url:https://dashscope.aliyuncs.com/compatible-mode
- Python爬虫实战:全方位爬取知乎学习板块问答数据
Python爬虫项目
2025年爬虫实战项目python爬虫学习开发语言scrapy游戏
1.项目背景与爬取目标知乎是中国最大的知识问答社区,聚集了大量高质量的学习资源和经验分享。爬取知乎“学习”板块的问答数据,可以为学习资料整理、舆情分析、推荐系统开发等提供数据支持。本项目目标:爬取“学习”话题下的热门问答列表抓取每个问答的标题、作者、回答内容、点赞数、评论数等详细信息实现动态加载内容的抓取,包含图片和富文本避免被反爬机制限制,保证数据采集稳定结合数据分析,为后续应用打基础2.知乎“
- Python爬虫实战:爬取知乎问答与用户信息
Python爬虫项目
python爬虫php数据分析开发语言开源
简介随着网络信息量的爆炸,如何有效获取有价值的内容,成为了数据分析、机器学习等领域的基础之一。爬虫作为数据采集的基本工具之一,常常被用来获取互联网上的公开数据。在这篇博客中,我们将结合最新的Python爬虫技术,详细讲解如何爬取知乎问答与用户信息。本文将会介绍:Python爬虫的基础知识知乎问答网页结构分析使用Python进行知乎数据爬取爬取知乎问答内容与用户信息如何处理和存储爬取的数据使用最新的
- 【机器学习&深度学习】反向传播机制
目录一、一句话定义二、类比理解三、为什重要?四、用生活例子解释:神经网络=烹饪机器人4.1第一步:尝一口(前向传播)4.2第二步:倒着推原因(反向传播)五、换成人工智能流程说一遍六、图示类比:找山顶(最优参数)七、总结一句人话八、PyTorch代码示例:亲眼看到每一层的梯度九、梯度=损失函数对参数的偏导数十、类比总结反向传播(Backpropagation)是神经网络中训练过程的核心机制,它就像“
- 遍历dom 并且存储(将每一层的DOM元素存在数组中)
换个号韩国红果果
JavaScripthtml
数组从0开始!!
var a=[],i=0;
for(var j=0;j<30;j++){
a[j]=[];//数组里套数组,且第i层存储在第a[i]中
}
function walkDOM(n){
do{
if(n.nodeType!==3)//筛选去除#text类型
a[i].push(n);
//con
- Android+Jquery Mobile学习系列(9)-总结和代码分享
白糖_
JQuery Mobile
目录导航
经过一个多月的边学习边练手,学会了Android基于Web开发的毛皮,其实开发过程中用Android原生API不是很多,更多的是HTML/Javascript/Css。
个人觉得基于WebView的Jquery Mobile开发有以下优点:
1、对于刚从Java Web转型过来的同学非常适合,只要懂得HTML开发就可以上手做事。
2、jquerym
- impala参考资料
dayutianfei
impala
记录一些有用的Impala资料
1. 入门资料
>>官网翻译:
http://my.oschina.net/weiqingbin/blog?catalog=423691
2. 实用进阶
>>代码&架构分析:
Impala/Hive现状分析与前景展望:http
- JAVA 静态变量与非静态变量初始化顺序之新解
周凡杨
java静态非静态顺序
今天和同事争论一问题,关于静态变量与非静态变量的初始化顺序,谁先谁后,最终想整理出来!测试代码:
import java.util.Map;
public class T {
public static T t = new T();
private Map map = new HashMap();
public T(){
System.out.println(&quo
- 跳出iframe返回外层页面
g21121
iframe
在web开发过程中难免要用到iframe,但当连接超时或跳转到公共页面时就会出现超时页面显示在iframe中,这时我们就需要跳出这个iframe到达一个公共页面去。
首先跳转到一个中间页,这个页面用于判断是否在iframe中,在页面加载的过程中调用如下代码:
<script type="text/javascript">
//<!--
function
- JAVA多线程监听JMS、MQ队列
510888780
java多线程
背景:消息队列中有非常多的消息需要处理,并且监听器onMessage()方法中的业务逻辑也相对比较复杂,为了加快队列消息的读取、处理速度。可以通过加快读取速度和加快处理速度来考虑。因此从这两个方面都使用多线程来处理。对于消息处理的业务处理逻辑用线程池来做。对于加快消息监听读取速度可以使用1.使用多个监听器监听一个队列;2.使用一个监听器开启多线程监听。
对于上面提到的方法2使用一个监听器开启多线
- 第一个SpringMvc例子
布衣凌宇
spring mvc
第一步:导入需要的包;
第二步:配置web.xml文件
<?xml version="1.0" encoding="UTF-8"?>
<web-app version="2.5"
xmlns="http://java.sun.com/xml/ns/javaee"
xmlns:xsi=
- 我的spring学习笔记15-容器扩展点之PropertyOverrideConfigurer
aijuans
Spring3
PropertyOverrideConfigurer类似于PropertyPlaceholderConfigurer,但是与后者相比,前者对于bean属性可以有缺省值或者根本没有值。也就是说如果properties文件中没有某个bean属性的内容,那么将使用上下文(配置的xml文件)中相应定义的值。如果properties文件中有bean属性的内容,那么就用properties文件中的值来代替上下
- 通过XSD验证XML
antlove
xmlschemaxsdvalidationSchemaFactory
1. XmlValidation.java
package xml.validation;
import java.io.InputStream;
import javax.xml.XMLConstants;
import javax.xml.transform.stream.StreamSource;
import javax.xml.validation.Schem
- 文本流与字符集
百合不是茶
PrintWrite()的使用字符集名字 别名获取
文本数据的输入输出;
输入;数据流,缓冲流
输出;介绍向文本打印格式化的输出PrintWrite();
package 文本流;
import java.io.FileNotFound
- ibatis模糊查询sqlmap-mapping-**.xml配置
bijian1013
ibatis
正常我们写ibatis的sqlmap-mapping-*.xml文件时,传入的参数都用##标识,如下所示:
<resultMap id="personInfo" class="com.bijian.study.dto.PersonDTO">
<res
- java jvm常用命令工具——jdb命令(The Java Debugger)
bijian1013
javajvmjdb
用来对core文件和正在运行的Java进程进行实时地调试,里面包含了丰富的命令帮助您进行调试,它的功能和Sun studio里面所带的dbx非常相似,但 jdb是专门用来针对Java应用程序的。
现在应该说日常的开发中很少用到JDB了,因为现在的IDE已经帮我们封装好了,如使用ECLI
- 【Spring框架二】Spring常用注解之Component、Repository、Service和Controller注解
bit1129
controller
在Spring常用注解第一步部分【Spring框架一】Spring常用注解之Autowired和Resource注解(http://bit1129.iteye.com/blog/2114084)中介绍了Autowired和Resource两个注解的功能,它们用于将依赖根据名称或者类型进行自动的注入,这简化了在XML中,依赖注入部分的XML的编写,但是UserDao和UserService两个bea
- cxf wsdl2java生成代码super出错,构造函数不匹配
bitray
super
由于过去对于soap协议的cxf接触的不是很多,所以遇到了也是迷糊了一会.后来经过查找资料才得以解决. 初始原因一般是由于jaxws2.2规范和jdk6及以上不兼容导致的.所以要强制降为jaxws2.1进行编译生成.我们需要少量的修改:
我们原来的代码
wsdl2java com.test.xxx -client http://.....
修改后的代
- 动态页面正文部分中文乱码排障一例
ronin47
公司网站一部分动态页面,早先使用apache+resin的架构运行,考虑到高并发访问下的响应性能问题,在前不久逐步开始用nginx替换掉了apache。 不过随后发现了一个问题,随意进入某一有分页的网页,第一页是正常的(因为静态化过了);点“下一页”,出来的页面两边正常,中间部分的标题、关键字等也正常,唯独每个标题下的正文无法正常显示。 因为有做过系统调整,所以第一反应就是新上
- java-54- 调整数组顺序使奇数位于偶数前面
bylijinnan
java
import java.util.Arrays;
import java.util.Random;
import ljn.help.Helper;
public class OddBeforeEven {
/**
* Q 54 调整数组顺序使奇数位于偶数前面
* 输入一个整数数组,调整数组中数字的顺序,使得所有奇数位于数组的前半部分,所有偶数位于数组的后半
- 从100PV到1亿级PV网站架构演变
cfyme
网站架构
一个网站就像一个人,存在一个从小到大的过程。养一个网站和养一个人一样,不同时期需要不同的方法,不同的方法下有共同的原则。本文结合我自已14年网站人的经历记录一些架构演变中的体会。 1:积累是必不可少的
架构师不是一天练成的。
1999年,我作了一个个人主页,在学校内的虚拟空间,参加了一次主页大赛,几个DREAMWEAVER的页面,几个TABLE作布局,一个DB连接,几行PHP的代码嵌入在HTM
- [宇宙时代]宇宙时代的GIS是什么?
comsci
Gis
我们都知道一个事实,在行星内部的时候,因为地理信息的坐标都是相对固定的,所以我们获取一组GIS数据之后,就可以存储到硬盘中,长久使用。。。但是,请注意,这种经验在宇宙时代是不能够被继续使用的
宇宙是一个高维时空
- 详解create database命令
czmmiao
database
完整命令
CREATE DATABASE mynewdb USER SYS IDENTIFIED BY sys_password USER SYSTEM IDENTIFIED BY system_password LOGFILE GROUP 1 ('/u01/logs/my/redo01a.log','/u02/logs/m
- 几句不中听却不得不认可的话
datageek
1、人丑就该多读书。
2、你不快乐是因为:你可以像猪一样懒,却无法像只猪一样懒得心安理得。
3、如果你太在意别人的看法,那么你的生活将变成一件裤衩,别人放什么屁,你都得接着。
4、你的问题主要在于:读书不多而买书太多,读书太少又特爱思考,还他妈话痨。
5、与禽兽搏斗的三种结局:(1)、赢了,比禽兽还禽兽。(2)、输了,禽兽不如。(3)、平了,跟禽兽没两样。结论:选择正确的对手很重要。
6
- 1 14:00 PHP中的“syntax error, unexpected T_PAAMAYIM_NEKUDOTAYIM”错误
dcj3sjt126com
PHP
原文地址:http://www.kafka0102.com/2010/08/281.html
因为需要,今天晚些在本机使用PHP做些测试,PHP脚本依赖了一堆我也不清楚做什么用的库。结果一跑起来,就报出类似下面的错误:“Parse error: syntax error, unexpected T_PAAMAYIM_NEKUDOTAYIM in /home/kafka/test/
- xcode6 Auto layout and size classes
dcj3sjt126com
ios
官方GUI
https://developer.apple.com/library/ios/documentation/UserExperience/Conceptual/AutolayoutPG/Introduction/Introduction.html
iOS中使用自动布局(一)
http://www.cocoachina.com/ind
- 通过PreparedStatement批量执行sql语句【sql语句相同,值不同】
梦见x光
sql事务批量执行
比如说:我有一个List需要添加到数据库中,那么我该如何通过PreparedStatement来操作呢?
public void addCustomerByCommit(Connection conn , List<Customer> customerList)
{
String sql = "inseret into customer(id
- 程序员必知必会----linux常用命令之十【系统相关】
hanqunfeng
Linux常用命令
一.linux快捷键
Ctrl+C : 终止当前命令
Ctrl+S : 暂停屏幕输出
Ctrl+Q : 恢复屏幕输出
Ctrl+U : 删除当前行光标前的所有字符
Ctrl+Z : 挂起当前正在执行的进程
Ctrl+L : 清除终端屏幕,相当于clear
二.终端命令
clear : 清除终端屏幕
reset : 重置视窗,当屏幕编码混乱时使用
time com
- NGINX
IXHONG
nginx
pcre 编译安装 nginx
conf/vhost/test.conf
upstream admin {
server 127.0.0.1:8080;
}
server {
listen 80;
&
- 设计模式--工厂模式
kerryg
设计模式
工厂方式模式分为三种:
1、普通工厂模式:建立一个工厂类,对实现了同一个接口的一些类进行实例的创建。
2、多个工厂方法的模式:就是对普通工厂方法模式的改进,在普通工厂方法模式中,如果传递的字符串出错,则不能正确创建对象,而多个工厂方法模式就是提供多个工厂方法,分别创建对象。
3、静态工厂方法模式:就是将上面的多个工厂方法模式里的方法置为静态,
- Spring InitializingBean/init-method和DisposableBean/destroy-method
mx_xiehd
javaspringbeanxml
1.initializingBean/init-method
实现org.springframework.beans.factory.InitializingBean接口允许一个bean在它的所有必须属性被BeanFactory设置后,来执行初始化的工作,InitialzingBean仅仅指定了一个方法。
通常InitializingBean接口的使用是能够被避免的,(不鼓励使用,因为没有必要
- 解决Centos下vim粘贴内容格式混乱问题
qindongliang1922
centosvim
有时候,我们在向vim打开的一个xml,或者任意文件中,拷贝粘贴的代码时,格式莫名其毛的就混乱了,然后自己一个个再重新,把格式排列好,非常耗时,而且很不爽,那么有没有办法避免呢? 答案是肯定的,设置下缩进格式就可以了,非常简单: 在用户的根目录下 直接vi ~/.vimrc文件 然后将set pastetoggle=<F9> 写入这个文件中,保存退出,重新登录,
- netty大并发请求问题
tianzhihehe
netty
多线程并发使用同一个channel
java.nio.BufferOverflowException: null
at java.nio.HeapByteBuffer.put(HeapByteBuffer.java:183) ~[na:1.7.0_60-ea]
at java.nio.ByteBuffer.put(ByteBuffer.java:832) ~[na:1.7.0_60-ea]
- Hadoop NameNode单点问题解决方案之一 AvatarNode
wyz2009107220
NameNode
我们遇到的情况
Hadoop NameNode存在单点问题。这个问题会影响分布式平台24*7运行。先说说我们的情况吧。
我们的团队负责管理一个1200节点的集群(总大小12PB),目前是运行版本为Hadoop 0.20,transaction logs写入一个共享的NFS filer(注:NetApp NFS Filer)。
经常遇到需要中断服务的问题是给hadoop打补丁。 DataNod