UVa OJ 197 - Cube (立方体)
Time limit: 30.000 seconds
限时30.000秒
Problem
问题
There was once a 3 by 3 by 3 cube built of 27 smaller cubes. It has fallen apart into seven pieces:
写曾经有一个3x3x3的立方块,由27个小立方块构成。它被切分为了如下七个碎片:
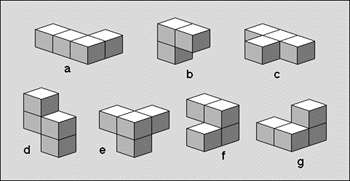
Figure 1: The seven pieces that once formed a cube
图1:组成立方体的七块碎片
The seven pieces can be assembled in many ways to again form the cube. Figure 2 shows one of these possibilities. The first square stands for the front plane, the next one for the middle plane and the last one for the back plane of the cube. The letters in the cells stand for the name of piece filling out the corresponding space in the cube. The name of the seven pieces can be found in figure 1.
这七个碎片可以由多种方式重新组成原先的立方块,图2给出了其中一种组装方法。第一个正方形代表前平面,下一个代表中平面,最后一个代表后平面。方格中的字母代表被放在对应位置上的碎片的名称。这七个碎片的名称可以在图1中看到。
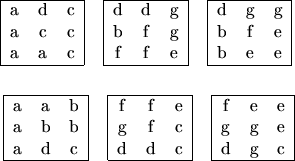
Figure 2: Two possibilities of assembling the cube
图2:由碎片组成立方体的两种可能方式
You are to write a program that outputs all possibilities of assembling the cube but suppress solutions that are mere rotations of another solution.
请你写一个程序输出组成立方体的所有可能方式,但不要输出仅仅是旋转角度不同的重复解。
Hint: Piece a is the only part that, by rotation and translation, cannot be transformed into itself. In order to avoid solutions that are mere rotations of an already found solution, you may restrict transformations of piece a to translations.
提示:碎片a是仅有一块不论如何旋转或平移都不可能变回原形的碎片,为避免重复计算仅旋转角度不同的多个解,你应当将a的变换限制为仅可平移。
Input
输入
The input file has several test cases. Each test case indicates the initial position of piece `a'. You can translate it, but you mustn't rotate it.
输入文件包含多个测试例子,每个测试例子指名了初始的‘a’的位置。你可以平移‘a’,但不能旋转。
Output
输出
For each solution found, your program should output a line containing the solution as a string. The string is a linearized form of the cube. Each letter stands for the piece filling out the corresponding space in the cube. It is linearized as follows:
对于找到的每一个解,你的程序应输出行包含解的字符串。该字符串是对立体的线性化。每个字母代表碎片填入立方体中的位置。以如下方式线性化:
- The string consists of substrings representing the front, middle and back plane.
- 字符串由三个子串构成,分别代表:前平面、中平面和后平面。
- Each substring consists of substrings representing the top, middle and bottom row.
- 每个子串又由三个子串构成,分别代表:顶行,中行和底行。
- Each row substring consists of letters representing the left, middle and right cell.
- 每行的子串又由三个字母构成,分别为左格,中格和右格。
The solutions in figure 2 would be represented like this:
图二所示的解表达如下:
adcaccaacddgbfgffedggbfebee
aababbadcffegfcddcfeeggedgc
It is very important that your program uses the naming convention given in figure 1 and linearizes the cube as explained above.
记住,你的程序一定要按照图1的命名约定来线性化立方体。
Print a blank line after each test case.
每一个测试例子结束后打印一行空行。
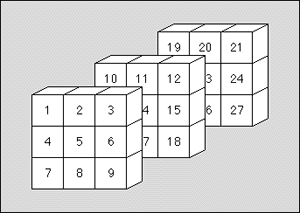
Figure 3: Positions of the cells in the string
图3:方格在字符串中的位置
Figure 3 again shows how the cells of the cube are linearized.
图3给出了立方体的方格被线性化的另一个示例。
Sample input
示例输入
aa.a..a....................
.........a..a..aa..........
Sample output
示例输出
aababbadcggeffcddcgeegfedfc
aababbadceffgdcgdceefedfggc
...
aababbadcffegfcddcfeeggedgc
adcaccaacfddfebgeeffdggbgeb
...
Analysis
分析
难题,对调试技巧要求高。
七块碎片的模式是由图中给定的,不能够改变它的形状。要求的解就是由这七块碎片以某种组合方式(不同的空间位置)来组合成为一个完整的立方体。题目给出的时间有30秒之多,这样看来就需要暴力搜索了。考虑立方体由27小块构成,根据题目中给出的线性化要求,每个小块对应的空间坐标是有其固定编号的。我们按照直角坐标系对每个小块标定整数坐标:
1: (0, 2, 2), 2: (1, 2, 2), 3: (2, 2, 2),
4: (0, 1, 2), 5: (1, 1, 2), 6: (2, 1, 2),
7: (0, 0, 2), 8: (1, 0, 2), 9: (2, 0, 2),
10: (0, 2, 1), 11: (1, 2, 1), 12: (2, 2, 1),
13: (0, 1, 1), 14: (1, 1, 1), 15: (2, 1, 1),
16: (0, 0, 1), 17: (1, 0, 1), 18: (2, 0, 1),
19: (0, 2, 1), 20: (1, 2, 1), 21: (2, 2, 1),
22: (0, 1, 1), 23: (1, 1, 1), 24: (2, 1, 1),
25: (0, 0, 1), 26: (1, 0, 1), 27: (2, 0, 1),
事实上,这些小块的坐标是可以用程序循环求出的,这里给出全部取值只是为了方便后面的算法描述。观察7块碎片,除b为3小块构成之外,其它均由4小块构成。这些碎片组成立方体时,其中的每个小块一定是位于(0, 0, 0)到(2, 2, 2)的坐标内的。这里要定义一个概念:构形。构形是指一个碎片在立方体中通过旋转或平移达到的一种形态,并且其每一个小块都没有超出立方体的坐标边界。如果用27个2进制数分别代表立方体中的27个坐标是否存在小方块(1表示对应位置有一个小方块,0表示没有),那么这27个数一定可以表示这7块碎片的任何一种构形。一个unsigned long型整数32位,足够表示任一块碎片的任一种形态。如果分别代表7块碎片的各自一种形态的7个2进制数:(b1 | b2 | b3 | b4 | b5 | b6 | b7) = 0x07ffffff,就说明7块碎片的这些形态完整的组成了立方体。设立方体c中没有放任何碎片时c=0,放入一个碎片b,即c:=c|b。如果b所需的位置在c中已经存在小方块,则有:~b & c != c。有了上述这些表达式方,填充算法的思路就很清晰了。我们只要生成每一种碎片的所有构形,然后用DFS的方式(深度为不同碎片)即可暴力搜索出所有可能的组合方式。
接下来的问是如何生成每一种碎片的所有构形。方式有很多种,这里采用三维坐标变换中的旋转矩阵方式,见维基百科:旋转矩阵。一个碎片的旋转有最多有24种不同的方式,事实上只有碎片a存在24种,其它的碎片的24种旋转中一定有一些转完的结果是相同的(这里需要一点空间想象力)。首先要构造这24种旋转矩阵(3x3矩阵),它们一定是x旋转、y旋转和z旋转的组合,每一种旋转的角度可选用0、π/2、π和-π/2。这样会生成64种矩阵,去重后就会剩下不同的24种。接下来以坐标的形式手动定义每一块碎片,然后求出每一块碎片的24种不同旋转(矩阵乘法)。这里要注意的时,不论是最初手动定义的碎片还是旋转后产生的新碎片,都要通过平移使之顶住立方体的x=0、y=0和z=0三个平面,也就是让他们在不越出坐标边界的前提下尽可能的靠近立方体的坐标原点。生成每一个碎片的所有旋转之后,就可以对这每一种旋转进行平移,从而得到每一个碎片的所有构形。
最后要注意几点:
- 你的小方块编号要与题目一致,注意建立正确的坐标系;
- 题目给的输出范例是错的,对于每一个输入,你的输出结果字符串要进行排序;
- 对于每一个输入的a的构形,你不能旋转,但一定要计算a的每一种可行平移的解,再汇总;
- 仔细优化递归函数,否则可能TLE;
- 先考虑设计完善的数据结构和代码结构,以免调试时找不着北。
Solution
解答
#include <algorithm>
#include <iostream>
#include <vector>
#include <string>
#include <memory.h>
struct POINT3 // 定义每个方块的坐标的结构体
{
int x;
int y;
int z;
};
typedef std::vector<POINT3> COORDS; // 类型定义,表示图中7个piece的坐标
typedef unsigned long FORMMASK; // 类型定义,表示每一个piece经过旋转、偏移之后产生的一种构型的掩码
typedef std::vector<FORMMASK> VECFORMMASK; // 类型定义,一个piece的掩码集合
typedef std::vector<VECFORMMASK> ALLPIECEFORMS; // 类型定义,所有piece的掩码集合
typedef std::vector<int> MATRIX; // 类型定义,表示矩阵
typedef std::vector<MATRIX> ROTMATS; // 类型定义,表示矩阵的集合
ALLPIECEFORMS allPieceForms; // 全局变量,存储所有piece经过旋转、偏移后的掩码
ALLPIECEFORMS result; // 全局变量,存储最终的结果
ROTMATS rotMats; // 全局变量,存储旋转矩阵
// 单位矩阵分别绕X、Y、Z轴旋转0°、90°、180°、270°后对应的矩阵
int rotateMatX[][9] = {
{1, 0, 0, 0, 1, 0, 0, 0, 1},
{1, 0, 0, 0, 0, -1, 0, 1, 0},
{1, 0, 0, 0, -1, 0, 0, 0, -1},
{1, 0, 0, 0, 0, 1, 0, -1, 0}
};
int rotateMatY[][9] = {
{1, 0, 0, 0, 1, 0, 0, 0, 1},
{0, 0, 1, 0, 1, 0, -1, 0, 0},
{-1, 0, 0, 0, 1, 0, 0, 0, -1},
{0, 0, -1, 0, 1, 0, 1, 0, 0}
};
int rotateMatZ[][9] = {
{1, 0, 0, 0, 1, 0, 0, 0, 1},
{0, -1, 0, 1, 0, 0, 0, 0, 1},
{-1, 0, 0, 0, -1, 0, 0, 0, 1},
{0, 1, 0, -1, 0, 0, 0, 0, 1}
};
// 题目图中7中piece相应的空间坐标,顺序为a,f,g,e,c,d,b,以左下角为原点(0,0,0)
POINT3 pieces[][4] = {
{{0, 0, 0}, {1, 0, 0}, {0, 1, 0}, {0, 2, 0}},
{{0, 0, 0}, {1, 0, 0}, {1, 0, 1}, {1, 1, 1}},
{{0, 0, 0}, {1, 0, 0}, {1, 0, 1}, {0, 1, 0}},
{{0, 0, 0}, {0, 0, 1}, {1, 0, 1}, {0, 1, 1}},
{{0, 1, 0}, {1, 0, 0}, {1, 1, 0}, {1, 2, 0}},
{{0, 0, 0}, {0, 0, 1}, {1, 0, 1}, {1, 0, 2}},
{{0, 0, 0}, {1, 0, 0}, {0, 0, 1},}
};
char nameMap[] = {'a', 'f', 'g', 'e', 'c', 'd', 'b'};
// 直角坐标系与题目坐标系的位置编号对应表
char posMap[] = {24, 25, 26, 21, 22, 23, 18, 19, 20, 15, 16, 17, 12, 13, 14, 9, 10, 11, 6, 7, 8, 3, 4, 5, 0, 1, 2};
bool operator < (const POINT3 &p1, const POINT3 &p2)
{
return (p1.x < p2.x || (p1.x == p2.x && p1.y < p2.y) ||
(p1.x == p2.x && p1.y == p2.y && p1.z < p2.z));
}
bool operator == (const POINT3 &p1, const POINT3 &p2)
{
return (p1.x == p2.x && p1.y == p2.y && p1.z == p2.z);
}
// 计算矩阵乘法,输入两个矩阵pM1,pM2,并输入第一个矩阵的行数,第二个矩阵的列数以及矩阵的大小,输出矩阵相乘的结果pR。
void MatMul(int *pM1, int *pM2, int r1, int c2, int n, int *pR)
{
for (int i = 0; i < r1; ++i) {
for (int j = 0; j < c2; ++j) {
pR[i * c2 + j] = 0;
for (int k = 0; k < n; ++k)
pR[i * c2 + j] += pM1[i * r1 + k] * pM2[k * c2 + j];
}
}
}
// 求坐标的相反数
POINT3 Inverse(POINT3 &coord)
{
coord.x = -coord.x;
coord.y = -coord.y;
coord.z = -coord.z;
return coord;
}
// 找出一个piece中坐标最大的点和坐标最小的点
void Bound(const COORDS &coords, POINT3 &min, POINT3 &max)
{
min = max = coords[0];
for (size_t i = 1; i < coords.size(); ++i) {
if (coords[i].x < min.x) min.x = coords[i].x;
if (coords[i].x > max.x) max.x = coords[i].x;
if (coords[i].y < min.y) min.y = coords[i].y;
if (coords[i].y > max.y) max.y = coords[i].y;
if (coords[i].z < min.z) min.z = coords[i].z;
if (coords[i].z > max.z) max.z = coords[i].z;
}
}
// 根据piece中坐标的最小值,标记一个piece进行偏移转换时能偏移的最大位置
void PieceSize(const COORDS &coords, POINT3 &size)
{
POINT3 minCoord;
Bound(coords, minCoord, size);
size.x -= minCoord.x;
size.y -= minCoord.y;
size.z -= minCoord.z;
}
// piece的偏移转换
void Translate(COORDS &coords, const POINT3 &dist)
{
for (size_t i = 0; i < coords.size(); ++i) {
coords[i].x += dist.x;
coords[i].y += dist.y;
coords[i].z += dist.z;
}
}
// 计算一个piece的掩码,根据piece中各个方块的位置坐标计算其在最终的结果序列中出现的位置。
FORMMASK Coords2Mask(COORDS &coords)
{
FORMMASK ulMask = 0;
for (COORDS::iterator j = coords.begin(); j != coords.end(); ++j) {
ulMask |= (1 << (j->x + j->y * 3 + j->z * 9));
}
return ulMask;
}
// 旋转、偏移转换3×3×3方块,forms记录给定piece的所有构型掩码
void ExpandForms(const POINT3 *pPiece, int n, VECFORMMASK &forms)
{
// 从数据指针构造坐标数组,并排序
COORDS coords(pPiece, pPiece + n), rotCoords(n);
POINT3 minCoord, size;
std::sort(coords.begin(), coords.end());
// rots记录给定piece的所有旋转
std::vector<COORDS> rots;
// 求出所有的旋转构型,包括不旋转的原构型(单位阵),每一个旋转构型最多有24个不同构型
for (ROTMATS::iterator i = rotMats.begin(); i != rotMats.end(); ++i) {
for (int j = 0; j < n; ++j) {
MatMul(i->data(), (int*)&coords[j], 3, 1, 3, (int*)&rotCoords[j]);
}
// 规格化每一种旋转构型,使旋转后的方块仍以左下角的小方块为原点
Bound(rotCoords, minCoord, size);
Translate(rotCoords, Inverse(minCoord));
std::sort(rotCoords.begin(), rotCoords.end());
rots.push_back(rotCoords);
}
// 去除重复的旋转构型
std::sort(rots.begin(), rots.end());
rots.erase(std::unique(rots.begin(), rots.end()), rots.end());
size_t nRotCnt = rots.size();
// 将每一种旋转构型偏移,产生新的偏移构型,每一个piece均有6个偏移构型
for (size_t i = 0; i != nRotCnt; ++i) {
PieceSize(rots[i], size);
for (minCoord.x = 0; minCoord.x < 3 - size.x; ++minCoord.x) {
for (minCoord.y = 0; minCoord.y < 3 - size.y; ++minCoord.y) {
for (minCoord.z = 0; minCoord.z < 3 - size.z; ++minCoord.z) {
if (minCoord.x != 0 || minCoord.y != 0 || minCoord.z != 0) {
rots.push_back(rots[i]);
Translate(rots.back(), minCoord);
}
}
}
}
}
// 计算相应构型的掩码
for (std::vector<COORDS>::iterator i = rots.begin(); i != rots.end(); ++i) {
forms.push_back(Coords2Mask(*i));
}
}
// 递归的查找题中的7种piece的组合结果,path中记录每一种组合的所有piece的掩码
void FillCube(ALLPIECEFORMS::const_iterator curForm, FORMMASK nCube, VECFORMMASK &path)
{
// 递归结束条件,每一种组合的掩码完全填充
if (nCube == 0x07ffffff) {
result.push_back(path);
return;
}
const FORMMASK *pForms = curForm->data();
size_t nFormCnt = curForm->size();
for (size_t i = 0; i < nFormCnt; ++i) {
// 判断当前的掩码中是否有某一piece的掩码,若没有,则修改当前掩码,并在path中记录piece
if (((~pForms[i]) & nCube) == nCube) {
unsigned long nTmpCube = nCube | pForms[i];
path.push_back(pForms[i]);
FillCube(curForm + 1, nTmpCube, path);
path.pop_back();
}
}
}
int main(void)
{
// 计算旋转矩阵,共计24种旋转情况,如:绕XY轴旋转90°,绕XZ轴旋转180°等
for (int i = 0; i < 4; ++i) {
for (int j = 0; j < 4; ++j) {
for (int k = 0; k < 4; ++k) {
int tmp1[9];
rotMats.push_back(std::vector<int>(9));
MatMul(rotateMatY[j], rotateMatZ[k], 3, 3, 3, tmp1);
MatMul(rotateMatX[i], tmp1, 3, 3, 3, rotMats.back().data());
}
}
}
std::sort(rotMats.begin(), rotMats.end());
rotMats.erase(std::unique(rotMats.begin(), rotMats.end()), rotMats.end());
// 初始化piece的所有旋转和偏移的构型
allPieceForms.resize(7);
for (int i = 0; i < 7; ++i) {
ExpandForms(pieces[i], 4 - (i / 6), allPieceForms[i]);
}
for (std::string strLine; getline(std::cin, strLine) && !strLine.empty(); )
{
// 计算读入的数据中a的位置
COORDS inputA;
result.clear();
for (std::string::iterator i = strLine.begin(); i != strLine.end(); ++i) {
if (*i == 'a') {
int nIdx = i - strLine.begin();
POINT3 tmp = {nIdx % 3, 2 - (nIdx % 9) / 3, 2 - nIdx / 9};
inputA.push_back(tmp);
}
}
// 将读入的pieceA的坐标规格化为空间直角坐标系并建立相应的掩码
POINT3 minCoord, tmp;
Bound(inputA, minCoord, tmp);
Translate(inputA, Inverse(minCoord));
std::sort(inputA.begin(), inputA.end());
Coords2Mask(inputA);
// 查找读入的pieceA转化到空间直角坐标系后相应的构型
int nRot = std::find(allPieceForms[0].begin(), allPieceForms[0].end(),
Coords2Mask(inputA)) - allPieceForms[0].begin();
// 计算pieceA对应的所有组合
FORMMASK fixedA = allPieceForms[0][nRot];
VECFORMMASK vfm(1, fixedA);
FillCube(allPieceForms.begin() + 1, fixedA, vfm);
// 计算pieceA经过偏移处理后的所有组合
for (int i = nRot * 5 + 24; i < (nRot + 1) * 5 + 24; ++i) {
fixedA = allPieceForms[0][i];
vfm = VECFORMMASK(1, fixedA);
FillCube(allPieceForms.begin() + 1, fixedA, vfm);
}
// 将所有掩码的组合转换为输出形式的字符串
std::vector<std::string> outStrs;
for (ALLPIECEFORMS::iterator i = result.begin(); i != result.end(); ++i) {
std::string str;
str.resize(27);
for (size_t j = 0; j < i->size(); ++j) {
FORMMASK mask = i->at(j);
for (size_t k = 0; k < 27; ++k) {
if (mask & (1 << posMap[k])) {
//判断条件中posMap[k]为将空间直角坐标系对应到题中坐标系的位置,调整输出字符串的顺序,与题中输出要求相符
str[k] = nameMap[j];
}
}
}
outStrs.push_back(str);
}
std::sort(outStrs.begin(), outStrs.end());
for (std::vector<std::string>::iterator i = outStrs.begin(); i != outStrs.end(); ++i) {
std::cout << *i << std::endl;
}
std::cout << std::endl;
}
return 0;
}