[zz] Principal Components Analysis (PCA) 主成分分析
我理解PCA应该分为2个过程:1.求出降维矩阵;2.利用得到的降维矩阵,对数据/特征做降维。
这里分成了两篇博客,来做总结。
http://matlabdatamining.blogspot.com/2010/02/principal-components-analysis.html
英文Principal Components Analysis的博客,这种思路挺好,但是有2处写错了,下面有标注。
http://www.cnblogs.com/denny402/p/4020831.html
这个中文的实现过程,跟上面的差不多。但解释的不够好。
Principal Components Analysis
Real-world data sets usually exhibit relationships among their variables. These relationships are often linear, or at least approximately so, making them amenable to common analysis techniques. One such technique is principal component analysis("PCA"), which rotates the original data to new coordinates, making the data as "flat" as possible.
Given a table of two or more variables, PCA generates a new table with the same number of variables, called the principal components. Each principal component is a linear transformation of the entire original data set. The coefficients of the principal components are calculated so that the first principal component contains the maximum variance (which we may tentatively think of as the "maximum information"). The second principal component is calculated to have the second most variance, and, importantly, is uncorrelated (in a linear sense) with the first principal component. Further principal components, if there are any, exhibit decreasing variance and are uncorrelated with all other principal components.
PCA is completely reversible (the original data may be recovered exactly from the principal components), making it a versatile tool, useful for data reduction, noise rejection, visualization and data compression among other things. This article walks through the specific mechanics of calculating the principal components of a data set in MATLAB, using either the MATLAB Statistics Toolbox, or just the base MATLAB product.
Performing Principal Components Analysis
Performing PCA will be illustrated using the following data set, which consists of 3 measurements taken of a particular subject over time:
>> A = [269.8 38.9 50.5
272.4 39.5 50.0
270.0 38.9 50.5
272.0 39.3 50.2
269.8 38.9 50.5
269.8 38.9 50.5
268.2 38.6 50.2
268.2 38.6 50.8
267.0 38.2 51.1
267.8 38.4 51.0
273.6 39.6 50.0
271.2 39.1 50.4
269.8 38.9 50.5
270.0 38.9 50.5
270.0 38.9 50.5
];
We determine the size of this data set thus:
>> [n m] = size(A)
n =
15
m =
3
To summarize the data, we calculate the sample mean vector and the sample standard deviation vector:
>> AMean = mean(A)
AMean =
269.9733 38.9067 50.4800
>> AStd = std(A)
AStd =
1.7854 0.3751 0.3144
Most often, the first step in PCA is to standardize the data. Here, "standardization" means subtracting the sample mean from each observation, then dividing by the sample standard deviation. This centers and scales the data. Sometimes there are good reasons for modifying or not performing this step, but I will recommend that you standardize unless you have a good reason not to. This is easy to perform, as follows:
>> B = (A - repmat(AMean,[n 1])) ./ repmat(AStd,[n 1])
B =
-0.0971 -0.0178 0.0636
1.3591 1.5820 -1.5266
0.0149 -0.0178 0.0636
1.1351 1.0487 -0.8905
-0.0971 -0.0178 0.0636
-0.0971 -0.0178 0.0636
-0.9932 -0.8177 -0.8905
-0.9932 -0.8177 1.0178
-1.6653 -1.8842 1.9719
-1.2173 -1.3509 1.6539
2.0312 1.8486 -1.5266
0.6870 0.5155 -0.2544
-0.0971 -0.0178 0.0636
0.0149 -0.0178 0.0636
0.0149 -0.0178 0.0636
>> C = A - repmat(AMean,[n 1]
-0.1733 -0.0067 0.0200
2.4267 0.5933 -0.4800
0.0267 -0.0067 0.0200
2.0267 0.3933 -0.2800
-0.1733 -0.0067 0.0200
-0.1733 -0.0067 0.0200
-1.7733 -0.3067 -0.2800
-1.7733 -0.3067 0.3200
-2.9733 -0.7067 0.6200
-2.1733 -0.5067 0.5200
3.6267 0.6933 -0.4800
1.2267 0.1933 -0.0800
-0.1733 -0.0067 0.0200
0.0267 -0.0067 0.0200
0.0267 -0.0067 0.0200
This calculation can also be carried out using the zscore function from the Statistics Toolbox:
>> B = zscore(A)
B =
-0.0971 -0.0178 0.0636
1.3591 1.5820 -1.5266
0.0149 -0.0178 0.0636
1.1351 1.0487 -0.8905
-0.0971 -0.0178 0.0636
-0.0971 -0.0178 0.0636
-0.9932 -0.8177 -0.8905
-0.9932 -0.8177 1.0178
-1.6653 -1.8842 1.9719
-1.2173 -1.3509 1.6539
2.0312 1.8486 -1.5266
0.6870 0.5155 -0.2544
-0.0971 -0.0178 0.0636
0.0149 -0.0178 0.0636
0.0149 -0.0178 0.0636
Calculating the coefficients of the principal components and their respective variances is done by finding the eigenfunctions of the sample covariance matrix:
>> [V D] = eig(cov(B))
V =
0.6505 0.4874 -0.5825
-0.7507 0.2963 -0.5904
-0.1152 0.8213 0.5587
D =
0.0066 0 0
0 0.1809 0
0 0 2.8125
应该是:
[V D] = eig(cov(C))
V =
0.1709 0.1808 -0.9686
-0.9646 -0.1698 -0.2019
-0.2010 0.9687 0.1454
D =
0.0015 0 0
0 0.0287 0
0 0 3.3971
The matrix V contains the coefficients for the principal components. The diagonal elements of D store the variance of the respective principal components. We can extract the diagonal like this:
>> diag(D)
ans =
0.0066
0.1809
2.8125
The coefficients and respective variances of the principal components could also be found using the princomp function from the Statistics Toolbox:
>> [COEFF SCORE LATENT] = princomp(B)
COEFF =
0.5825 -0.4874 0.6505
0.5904 -0.2963 -0.7507
-0.5587 -0.8213 -0.1152
SCORE =
-0.1026 0.0003 -0.0571
2.5786 0.1226 -0.1277
-0.0373 -0.0543 0.0157
1.7779 -0.1326 0.0536
-0.1026 0.0003 -0.0571
-0.1026 0.0003 -0.0571
-0.5637 1.4579 0.0704
-1.6299 -0.1095 -0.1495
-3.1841 -0.2496 0.1041
-2.4306 -0.3647 0.0319
3.1275 -0.2840 0.1093
0.8467 -0.2787 0.0892
-0.1026 0.0003 -0.0571
-0.0373 -0.0543 0.0157
-0.0373 -0.0543 0.0157
LATENT =
2.8125
0.1809
0.0066
应该是:
>> [COEFF SCORE LATENT] = princomp(A)
COEFF =
0.9686 0.1808 -0.1709
0.2019 -0.1698 0.9646
-0.1454 0.9687 0.2010
SCORE =
-0.1721 -0.0108 0.0272
2.5399 -0.1270 0.0612
0.0216 0.0253 -0.0070
2.0831 0.0284 -0.0232
-0.1721 -0.0108 0.0272
-0.1721 -0.0108 0.0272
-1.7388 -0.5398 -0.0491
-1.8260 0.0414 0.0715
-3.1127 0.1830 -0.0490
-2.2829 0.1968 -0.0129
3.7224 0.0730 -0.0473
1.2388 0.1115 -0.0392
-0.1721 -0.0108 0.0272
0.0216 0.0253 -0.0070
0.0216 0.0253 -0.0070
LATENT =
3.3971
0.0287
0.0015
Note three important things about the above:
1. The order of the principal components from princomp is opposite of that from eig(cov(B)). princomp orders the principal components so that the first one appears in column 1, whereas eig(cov(B)) stores it in the last column.
2. Some of the coefficients from each method have the opposite sign. This is fine: There is no "natural" orientation for principal components, so you can expect different software to produce different mixes of signs.
3. SCORE contains the actual principal components, as calculated by princomp.
To calculate the principal components without princomp, simply multiply the standardized data by the principal component coefficients:
>> B * COEFF
ans =
-0.1026 0.0003 -0.0571
2.5786 0.1226 -0.1277
-0.0373 -0.0543 0.0157
1.7779 -0.1326 0.0536
-0.1026 0.0003 -0.0571
-0.1026 0.0003 -0.0571
-0.5637 1.4579 0.0704
-1.6299 -0.1095 -0.1495
-3.1841 -0.2496 0.1041
-2.4306 -0.3647 0.0319
3.1275 -0.2840 0.1093
0.8467 -0.2787 0.0892
-0.1026 0.0003 -0.0571
-0.0373 -0.0543 0.0157
-0.0373 -0.0543 0.0157
To reverse this transformation, simply multiply by the transpose of the coefficent matrix:
>> (B * COEFF) * COEFF'
ans =
-0.0971 -0.0178 0.0636
1.3591 1.5820 -1.5266
0.0149 -0.0178 0.0636
1.1351 1.0487 -0.8905
-0.0971 -0.0178 0.0636
-0.0971 -0.0178 0.0636
-0.9932 -0.8177 -0.8905
-0.9932 -0.8177 1.0178
-1.6653 -1.8842 1.9719
-1.2173 -1.3509 1.6539
2.0312 1.8486 -1.5266
0.6870 0.5155 -0.2544
-0.0971 -0.0178 0.0636
0.0149 -0.0178 0.0636
0.0149 -0.0178 0.0636
Finally, to get back to the original data, multiply each observation by the sample standard deviation vector and add the mean vector:
>> ((B * COEFF) * COEFF') .* repmat(AStd,[n 1]) + repmat(AMean,[n 1])
ans =
269.8000 38.9000 50.5000
272.4000 39.5000 50.0000
270.0000 38.9000 50.5000
272.0000 39.3000 50.2000
269.8000 38.9000 50.5000
269.8000 38.9000 50.5000
268.2000 38.6000 50.2000
268.2000 38.6000 50.8000
267.0000 38.2000 51.1000
267.8000 38.4000 51.0000
273.6000 39.6000 50.0000
271.2000 39.1000 50.4000
269.8000 38.9000 50.5000
270.0000 38.9000 50.5000
270.0000 38.9000 50.5000
This completes the round trip from the original data to the principal components and back to the original data. In some applications, the principal components are modified before the return trip.
Let's consider what we've gained by making the trip to the principal component coordinate system. First, more variance has indeed been squeezed in the first principal component, which we can see by taking the sample variance of principal components:
>> var(SCORE)
ans =
2.8125 0.1809 0.0066
The cumulative variance contained in the first so many principal components can be easily calculated thus:
>> cumsum(var(SCORE)) / sum(var(SCORE))
ans =
0.9375 0.9978 1.0000
Interestingly in this case, the first principal component contains nearly 94% of the variance of the original table. A lossy data compression scheme which discarded the second and third principal components would compress 3 variables into 1, while losing only 6% of the variance.
The other important thing to note about the principal components is that they are completely uncorrelated (as measured by the usual Pearson correlation), which we can test by calculating their correlation matrix:
>> corrcoef(SCORE)
ans =
1.0000 -0.0000 0.0000
-0.0000 1.0000 -0.0000
0.0000 -0.0000 1.0000
Discussion
PCA "squeezes" as much information (as measured by variance) as possible into the first principal components. In some cases the number of principal components needed to store the vast majority of variance is shockingly small: a tremendous feat of data manipulation. This transformation can be performed quickly on contemporary hardware and is invertible, permitting any number of useful applications.
For the most part, PCA really is as wonderful as it seems. There are a few caveats, however:
1. PCA doesn't always work well, in terms of compressing the variance. Sometimes variables just aren't related in a way which is easily exploited by PCA. This means that all or nearly all of the principal components will be needed to capture the multivariate variance in the data, making the use of PCA moot.
2. Variance may not be what we want condensed into a few variables. For example, if we are using PCA to reduce data for predictive model construction, then it is not necessarily the case that the first principal components yield a better model than the last principal components (though it often works out more or less that way).
3. PCA is built from components, such as the sample covariance, which are not statistically robust. This means that PCA may be thrown off by outliers and other data pathologies. How seriously this affects the result is specific to the data and application.
4. Though PCA can cram much of the variance in a data set into fewer variables, it still requires all of the variables to generate the principal components of future observations. Note that this is true, regardless of how many principal components are retained for the application. PCA is not a subset selection procedure, and this may have important logistical implications.
http://blog.pluskid.org/?p=290
这篇博客对pca理解的很深刻。
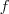 是降维函数,如果是降为 2 维,那么我希望第 2 维去关注第 1 维之外的 variance ,所以要求它在与第一维垂直的情况下也达到 variance 最大化。以此类推。
是降维函数,如果是降为 2 维,那么我希望第 2 维去关注第 1 维之外的 variance ,所以要求它在与第一维垂直的情况下也达到 variance 最大化。以此类推。
然而,当我们把降维函数 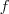 限定维线性的时候,两种途径会得到同样的结果,就是被广泛使用的 Principal Components Analysis(PCA) 。PCA 的降维函数是线性的,可以用一个
限定维线性的时候,两种途径会得到同样的结果,就是被广泛使用的 Principal Components Analysis(PCA) 。PCA 的降维函数是线性的,可以用一个 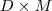 维的矩阵
维的矩阵 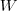 来表示,因此,一个 D 维的向量
来表示,因此,一个 D 维的向量  经过线性变换
经过线性变换 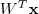 之后得到一个 M 维向量,就是降维的结果。把原始数据按行排列为一个
之后得到一个 M 维向量,就是降维的结果。把原始数据按行排列为一个 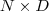 维的矩阵
维的矩阵 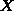 ,则
,则 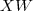 就是降维后的
就是降维后的  维的数据矩阵,目标是使其 covariance 矩阵最大。在数据被规则化(即减去其平均值)过的情况下,协方差矩阵 (covariance)
维的数据矩阵,目标是使其 covariance 矩阵最大。在数据被规则化(即减去其平均值)过的情况下,协方差矩阵 (covariance) 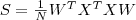 ,当然矩阵不是一个数,不能直接最大化,如果我们采用矩阵的 Trace (亦即其对角线上元素的和)来衡量其大小的话,要对
,当然矩阵不是一个数,不能直接最大化,如果我们采用矩阵的 Trace (亦即其对角线上元素的和)来衡量其大小的话,要对 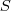 求最大化,只需要求出
求最大化,只需要求出 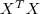 的特征值和特征向量,将 M 个最大的特征值所对应的特征向量按列排列起来组成线性变换矩阵
的特征值和特征向量,将 M 个最大的特征值所对应的特征向量按列排列起来组成线性变换矩阵 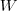 即可。这也就是 PCA 的求解过程,得到的降维矩阵
即可。这也就是 PCA 的求解过程,得到的降维矩阵 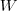 可以直接用到新的数据上。如果熟悉 Latent Semantic Analysis (LSA) 的话,大概已经看出 PCA 和 Singular Value Decomposition (SVD) 以及 LSA 之间的关系了。
可以直接用到新的数据上。如果熟悉 Latent Semantic Analysis (LSA) 的话,大概已经看出 PCA 和 Singular Value Decomposition (SVD) 以及 LSA 之间的关系了。
还有,别忘了wiki。