Prolog学习：数独和八皇后问题

上一篇简单介绍了下Prolog的一些基本概念，今天我们来利用这些基本概念解决两个问题：数独和八皇后问题。

数独

 数独是一个很经典的游戏：

玩家需要根据n×n盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫内的数字均含1-n，不重复。

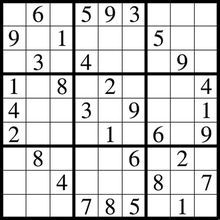
当然数独的阶有很多，9×9是最常见的，我们就以它做例子。在用Prolog解决之前先想想如果我们用C#或Java来做或怎么做？无非就是数据结构加算法，我们先得用一个数据结构表示数独，然后我们要在这个数据结构上“施加”算法进行求解。采用Prolog的第一步是相同的，我们得找一个数据结构表示数独，毫无疑问在Prolog中我们只能选择列表或元组，这里列表是更好的选择，因为列表可以进行[Head|Tail]解析，后面你就知道为什么了。我们像下面这样表示一个数独：

[_, 6, _, 5, 9, 3, _, _, _,

 9, _, 1, _, _, _, 5, _, _,

 _, 3, _, 4, _, _, _, 9, _,

 1, _, 8, _, 2, _, _, _, 4,

 4, _, _, 3, _, 9, _, _, 1,

 2, _, _, _, 1, _, 6, _, 9,

 _, 8, _, _, _, 6, _, 2, _,

 _, _, 4, _, _, _, 8, _, 7,

 _, _, _, 7, 8, 5, _, 1, _] 

“_”代表未知的数字，需要玩家填空的地方。

接下来的步骤跟命令式语言就截然不同了，我们不是描述算法，而是要描述数独这个游戏的规则：

1. 给定玩家一个9×9的盘面，玩家填充完所有的空格后最终的解仍然是这个9×9的盘面；
2. 填充完空格后，每一个空格内的数字均在1~9之内；
3. 填充完空格后，每一行9个数字各不相同；
4. 填充完空格后，每一列9个数字各不相同；
5. 填充完空格后，每一个宫格内的数字各不相同。

Ok，这就是整个游戏的规则。你可能觉得第一条规则没什么用，实际上第一条规则定义了“解”的形式，就像在C#中我们确定了方法的签名一样：

sudoku(Puzzle,Solution):- Solution = Puzzle.

事实上这个规则已经可以工作了：

| ?- sudoku([1,2,3,4,5,6,7,8,9,

             1,2,3,4,5,6,7,8,9, 

             1,2,3,4,5,6,7,8,9, 

             1,2,3,4,5,6,7,8,9,

             1,2,3,4,5,6,7,8,9,

             1,2,3,4,5,6,7,8,9,

             1,2,3,4,5,6,7,8,9,

             1,2,3,4,5,6,7,8,9,

             1,2,3,4,5,6,7,8,9],Solution). 



Solution = [1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9,1,2,3,4,5,6,7,8,9......

当然这只是第一步，这个规则对于输入的数独形式没有任何限制，事实上可以是任意的列表,Prolog都返回yes：

| ?- sudoku([1,2,3],Solution).



Solution = [1,2,3]



yes

我们需要规定下数独的形式：

sudoku(Puzzle,Solution):-

    Solution = Puzzle,

    Puzzle = [S11,S12,S13,S14,S15,S16,S17,S18,S19,

              S21,S22,S23,S24,S25,S26,S27,S28,S29,

              S31,S32,S33,S34,S35,S36,S37,S38,S39,

              S41,S42,S43,S44,S45,S46,S47,S48,S49,

              S51,S52,S53,S54,S55,S56,S57,S58,S59,

              S61,S62,S63,S64,S65,S66,S67,S68,S69,

              S71,S72,S73,S74,S75,S76,S77,S78,S79,

              S81,S82,S83,S84,S85,S86,S87,S88,S89,

              S91,S92,S93,S94,S95,S96,S97,S98,S99].

| ?- sudoku([1,2,3],Solution).



no

我们接着看第二条规则：“填充完空格后，每一个空格内的数字均在1~9之内” 。上一篇文章中我们介绍了Prolog中有一个内置谓词叫fd_domain，这时候就可以派上用场了：

sudoku(Puzzle,Solution):-

    Solution = Puzzle,

    Puzzle = [S11,S12,S13,S14,S15,S16,S17,S18,S19,

              S21,S22,S23,S24,S25,S26,S27,S28,S29,

              S31,S32,S33,S34,S35,S36,S37,S38,S39,

              S41,S42,S43,S44,S45,S46,S47,S48,S49,

              S51,S52,S53,S54,S55,S56,S57,S58,S59,

              S61,S62,S63,S64,S65,S66,S67,S68,S69,

              S71,S72,S73,S74,S75,S76,S77,S78,S79,

              S81,S82,S83,S84,S85,S86,S87,S88,S89,

              S91,S92,S93,S94,S95,S96,S97,S98,S99],

    fd_domain(Puzzle,1,9).

好了现在我们只能输入9×9并且每个每个位置上只能是1~9之间的数的列表了。

好了，现在到整个游戏的关键规则，事实上2,3,4这三个规则才决定了数独的难度，1,2只不过是基础，我们来统一考虑这三个问题。这里其实比想象的简单多了。我们首先要做的就是需要定义出来行、列、宫格：

Row1 = [S11,S12,S13,S14,S15,S16,S17,S18,S19],

Row2 = [S21,S22,S23,S24,S25,S26,S27,S28,S29],

Row3 = [S31,S32,S33,S34,S35,S36,S37,S38,S39],

Row4 = [S41,S42,S43,S44,S45,S46,S47,S48,S49],

Row5 = [S51,S52,S53,S54,S55,S56,S57,S58,S59],

Row6 = [S61,S62,S63,S64,S65,S66,S67,S68,S69],

Row7 = [S71,S72,S73,S74,S75,S76,S77,S78,S79],

Row8 = [S81,S82,S83,S84,S85,S86,S87,S88,S89],

Row9 = [S91,S92,S93,S94,S95,S96,S97,S98,S99],

    

Col1 = [S11,S21,S31,S41,S51,S61,S71,S81,S91],

Col2 = [S12,S22,S32,S42,S52,S62,S72,S82,S92],

Col3 = [S13,S23,S33,S43,S53,S63,S73,S83,S93],

Col4 = [S14,S24,S34,S44,S54,S64,S74,S84,S94],

Col5 = [S15,S25,S35,S45,S55,S65,S75,S85,S95],

Col6 = [S16,S26,S36,S46,S56,S66,S76,S86,S96],

Col7 = [S17,S27,S37,S47,S57,S67,S77,S87,S97],

Col8 = [S18,S28,S38,S48,S58,S68,S78,S88,S98],

Col9 = [S19,S29,S39,S49,S59,S69,S79,S89,S99],

    

Square1 = [S11,S12,S13,S21,S22,S23,S31,S32,S33],

Square2 = [S14,S15,S16,S24,S25,S26,S34,S35,S36],

Square3 = [S17,S18,S19,S27,S28,S29,S37,S38,S39],

Square4 = [S41,S42,S43,S51,S52,S53,S61,S62,S63],

Square5 = [S44,S45,S46,S54,S55,S56,S64,S65,S66],

Square6 = [S47,S48,S49,S57,S58,S59,S67,S68,S69],

Square7 = [S71,S72,S73,S81,S82,S83,S91,S92,S93],

Square8 = [S74,S75,S76,S84,S85,S86,S94,S95,S96],

Square9 = [S77,S78,S79,S87,S88,S89,S97,S98,S99],

上一篇文章中我还提到一个谓词叫fd_all_different:检查列表中是否有重复元素，接下来我们只要证明每一列，每一行，每一个宫格列表内没有重复元素就可以了：

fd_all_different(Row1),

fd_all_different(Row2),

……

fd_all_different(Col1),

fd_all_different(Col2),

……

fd_all_different(Square1),

fd_all_different(Square2),

……

其实到此这个解数独的程序已经结束了，不过最后这几行代码太土了，我们可以采用用递归“优化”下，像下面这样：

valid([]).

valid([Head|Tail]):-

    fd_all_different(Head),

    valid(Tail).

valid([Row1,Row2,Row3,Row4,Row5,Row6,Row7,Row8,Row9,

          Col1,Col2,Col3,Col4,Col5,Col6,Col7,Col8,Col9,

          Square1,Square2,Square3,Square4,Square5,Square6,Square7,Square8,Square9]).

不管你信不信，我们已经搞定了，最终完整的代码如下：

valid([]).

valid([Head|Tail]):-

    fd_all_different(Head),

    valid(Tail).

sudoku(Puzzle,Solution):-

    Solution = Puzzle,

    Puzzle = [S11,S12,S13,S14,S15,S16,S17,S18,S19,

          S21,S22,S23,S24,S25,S26,S27,S28,S29,

          S31,S32,S33,S34,S35,S36,S37,S38,S39,

          S41,S42,S43,S44,S45,S46,S47,S48,S49,

          S51,S52,S53,S54,S55,S56,S57,S58,S59,

          S61,S62,S63,S64,S65,S66,S67,S68,S69,

          S71,S72,S73,S74,S75,S76,S77,S78,S79,

          S81,S82,S83,S84,S85,S86,S87,S88,S89,

          S91,S92,S93,S94,S95,S96,S97,S98,S99],

    fd_domain(Puzzle,1,9),

    

    Row1 = [S11,S12,S13,S14,S15,S16,S17,S18,S19],

    Row2 = [S21,S22,S23,S24,S25,S26,S27,S28,S29],

    Row3 = [S31,S32,S33,S34,S35,S36,S37,S38,S39],

    Row4 = [S41,S42,S43,S44,S45,S46,S47,S48,S49],

    Row5 = [S51,S52,S53,S54,S55,S56,S57,S58,S59],

    Row6 = [S61,S62,S63,S64,S65,S66,S67,S68,S69],

    Row7 = [S71,S72,S73,S74,S75,S76,S77,S78,S79],

    Row8 = [S81,S82,S83,S84,S85,S86,S87,S88,S89],

    Row9 = [S91,S92,S93,S94,S95,S96,S97,S98,S99],

    

    Col1 = [S11,S21,S31,S41,S51,S61,S71,S81,S91],

    Col2 = [S12,S22,S32,S42,S52,S62,S72,S82,S92],

    Col3 = [S13,S23,S33,S43,S53,S63,S73,S83,S93],

    Col4 = [S14,S24,S34,S44,S54,S64,S74,S84,S94],

    Col5 = [S15,S25,S35,S45,S55,S65,S75,S85,S95],

    Col6 = [S16,S26,S36,S46,S56,S66,S76,S86,S96],

    Col7 = [S17,S27,S37,S47,S57,S67,S77,S87,S97],

    Col8 = [S18,S28,S38,S48,S58,S68,S78,S88,S98],

    Col9 = [S19,S29,S39,S49,S59,S69,S79,S89,S99],

    

    Square1 = [S11,S12,S13,S21,S22,S23,S31,S32,S33],

    Square2 = [S14,S15,S16,S24,S25,S26,S34,S35,S36],

    Square3 = [S17,S18,S19,S27,S28,S29,S37,S38,S39],

    Square4 = [S41,S42,S43,S51,S52,S53,S61,S62,S63],

    Square5 = [S44,S45,S46,S54,S55,S56,S64,S65,S66],

    Square6 = [S47,S48,S49,S57,S58,S59,S67,S68,S69],

    Square7 = [S71,S72,S73,S81,S82,S83,S91,S92,S93],

    Square8 = [S74,S75,S76,S84,S85,S86,S94,S95,S96],

    Square9 = [S77,S78,S79,S87,S88,S89,S97,S98,S99],

    

    valid(Row1,Row2,Row3,Row4,Row5,Row6,Row7,Row8,Row9,

          Col1,Col2,Col3,Col4,Col5,Col6,Col7,Col8,Col9,

          Square1,Square2,Square3,Square4,Square5,Square6,Square7,Square8,Square9).

反正我信了，我们来试试吧，就以上面我从百度上找到的那个图为例：

| ?- sudoku([_, 6, _, 5, 9, 3, _, _, _,

 9, _, 1, _, _, _, 5, _, _,

 _, 3, _, 4, _, _, _, 9, _,

 1, _, 8, _, 2, _, _, _, 4,

 4, _, _, 3, _, 9, _, _, 1,

 2, _, _, _, 1, _, 6, _, 9,

 _, 8, _, _, _, 6, _, 2, _,

 _, _, 4, _, _, _, 8, _, 7,

 _, _, _, 7, 8, 5, _, 1, _],Solution).



Solution = [7,6,2,5,9,3,1,4,8,9,4,1,2,7,8,5,3,6,8,3,5,4,6,1,7,9,2,1,9,8,6,2,7,3,5,4,4,7,6,3,5,9,2,8,1,2,5,3,8,1,4,6,7,9,3,8,7,1,4,6,9,2,5,5,1,4,9,3,2,8,6,7,6,2,9,7,8,5,4,1,3]

美化后的结果是这样的：

[7,6,2,5,9,3,1,4,8,

 9,4,1,2,7,8,5,3,6,

 8,3,5,4,6,1,7,9,2,

 1,9,8,6,2,7,3,5,4,

 4,7,6,3,5,9,2,8,1,

 2,5,3,8,1,4,6,7,9,

 3,8,7,1,4,6,9,2,5,

 5,1,4,9,3,2,8,6,7,

 6,2,9,7,8,5,4,1,3]

Perfect!

 

八皇后问题

Ok，有了数独问题作为铺垫，下面看八皇后问题应该就应该没那么难了，请保持用Prolog思考问题的方式，解决后你会发现Prolog真是这方面的“专家”，Let's Go!

八皇后问题也是一个非常经典的问题：

八皇后问题是一个以国际象棋为背景的问题：如何能够在 8×8 的国际象棋棋盘上放置八个皇后，使得任何一个皇后都无法直接吃掉其他的皇后？为了达到此目的，任两个皇后都不能处于同一条横行、纵行或斜线上。

老套路我们先描述游戏规则。

1. 每个皇后有一个行号和列号，行号和列号的取值范围在1~8之间；
2. 一个棋盘上有八个皇后；
3. 任意两个皇后不可以共享一行；
4. 任意两个皇后不可以共享一列；
5. 任意两个皇后不可以在同一个对角线上（左下角->右上角）；
6. 任意两个皇后不可以在同一个对角线上（右下角->左上角）。

在了解规则之后我们梳理一下这个问题，对照上面这个图：

我们给棋盘上每一个位置设定一个坐标(x,y)，八个皇后的坐标分别为(x1,y1)，(x2,y2)……我们以回溯的角度看问题，假设如图已经得到了最后解，那么这8个坐标满足：x1，x2……各不相同，y1，y2……个不相同，找出(x1,y1)，(x2,y2)……中属于对角线1上的和对角线2上的位置，它们坐标应该个不相同。

(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(1,7),(1,8)

(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),(2,7),(2,8)

(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(3,7),(3,8)

(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(4,7),(4,8)

(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),(5,7),(5,8)

(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),(6,7),(6,8)

(7,1),(7,2),(7,3),(7,4),(7,5),(7,6),(7,7),(7,8)

(8,1),(8,2),(8,3),(8,4),(8,5),(8,6),(8,7),(8,8)

所以整个问题的难点在于给定类似下面这样一个列表，我们需要找出其中的所有的行号，列号，和在对角线上的坐标：

[(1,1),(1,5),(2,5),(2,2),(8,8),(4,4),(4,5),(5,4)]

找出行号和列号稍微简单点，这里直接给出答案，大家也可以自己思考下：

rows([],[]).

rows([(Row,_)|QueensTail],[Row|RowsTail]):-

    rows(QueensTail,RowsTail).

cols([],[]).

cols([(_,Col)|QueensTail],[Col|ColsTail]):-

	cols(QueensTail,ColsTail).

把上面的列表代进去简单验证下：

| ?- rows([(1,1),(1,5),(2,5),(2,2),(8,8),(4,4),(4,5),(5,4)],Rows).



Rows = [1,1,2,2,8,4,4,5]



yes

| ?- cols([(1,1),(1,5),(2,5),(2,2),(8,8),(4,4),(4,5),(5,4)],Cols).



Cols = [1,5,5,2,8,4,5,4]



yes

关键是如何验证对角线上的元素，而且两条对角线是不一样的，提醒下因为我们最后会还是会利用fd_all_different这个谓词。

 

好吧，我们回过头观察下上面那个棋盘的坐标图（注意我标红的地方），有没有发现什么规则呢？

• 左上角到右下角的对角线上的元素：所有坐标的横坐标-纵坐标都相同，等于0；
• 左下角到右上角的对角线上的元素：所有坐标的横坐标+纵坐标都相同，等于9；

OK，我们可以定义下面这样两个谓词diags1和diags2：

diags1([],[]).

diags1([(Row,Col)|QueensTail],[Diagonal|DiagonalsTail]):-

    Diagonal is Col - Row,

    diags1(QueensTail,DiagonalsTail).

diags2([],[]).

diags2([(Row,Col)|QueensTail],[Diagonal|DiagonalsTail]):-

    Diagonal is Col + Row,

    diags2(QueensTail,DiagonalsTail).

我们可以简单验证下：

| ?- diags1([(2,2),(8,8)],Diags1).



Diags1 = [0,0]



yes

 | ?- diags2([(4,5),(5,4)],Diags2).

 Diags2 = [9,9]

 yes

如果坐标在对角线上，那么抓取到的列表元素都是相等的。

好了，到目前为止我们已经完成了最难的部分，剩下的都是一些验证性工作。我们最终的“程序入口”应该是这样的：

eight_queens([(X1,Y1),(X2,Y2),(X3,Y3),(X4,Y4),(X5,Y5),(X6,Y6),(X7,Y7),(X8,Y8)])

我们还需要一些验证性工作：

1.给定列表里的皇后是不是合法的，即横纵坐标都在1~8之内，这用到了我上一篇中提到的member谓词：

valid_queen((Row,Col)):-

    Range = [1,2,3,4,5,6,7,8],

    member(Row,Range),member(Col,Range).

2.验证给定的列表是不是八个皇后，这里用到一个length谓词，顾名思义：

length(Board,8).

3.需要递归的验证给定的列表中的每个元素是不是“皇后”：

valid_board([]).

valid_board([Head|Tail]):- valid_queen(Head),valid_board(Tail).

Ok，下面就是八皇后问题的答案的完整代码：

valid_queen((Row,Col)):-

    Range = [1,2,3,4,5,6,7,8],

    member(Row,Range),member(Col,Range).



valid_board([]).

valid_board([Head|Tail]):- valid_queen(Head),valid_board(Tail).



rows([],[]).

rows([(Row,_)|QueensTail],[Row|RowsTail]):-

    rows(QueensTail,RowsTail).



cols([],[]).

cols([(_,Col)|QueensTail],[Col|ColsTail]):-

    cols(QueensTail,ColsTail).

    

diags1([],[]).

diags1([(Row,Col)|QueensTail],[Diagonal|DiagonalsTail]):-

    Diagonal is Col - Row,

    diags1(QueensTail,DiagonalsTail).

    

diags2([],[]).

diags2([(Row,Col)|QueensTail],[Diagonal|DiagonalsTail]):-

    Diagonal is Col + Row,

    diags2(QueensTail,DiagonalsTail).



eight_queens(Board) :-

    length(Board,8),

    valid_board(Board),

    

    rows(Board,Rows),

    cols(Board,Cols),

    diags1(Board,Diags1),

    diags2(Board,Diags2),

    

    fd_all_different(Rows),

    fd_all_different(Cols),

    fd_all_different(Diags1),

    fd_all_different(Diags2).   

没错，答案已经出来，但事实上上面这个程序运行的非常慢，我在我i7的笔记本上的GNU Prolog中执行下面这个问题，半天没有响应：

| ?- eight_queens([(X1,Y1),(X2,Y2),(X3,Y3),(X4,Y4),(X5,Y5),(X6,Y6),(X7,Y7),(X8,Y8)]).

其实我们可以对这个问题进行一个简化。我们可以肯定棋盘上八行每行肯定有一个皇后，又因为互不能在一行，因此我们假设八皇后的坐标分别为：(1,A),(2,B),(3,C),(4,D),(5,E),(6,F),(7,G),(8,H)。那么我们可以对上面的代码进行优化，去掉所有对行的操作，优化后代码如下：

valid_queen((Row,Col)):- member(Col,[1,2,3,4,5,6,7,8]).



valid_board([]).

valid_board([Head|Tail]):- valid_queen(Head),valid_board(Tail).



cols([],[]).

cols([(_,Col)|QueensTail],[Col|ColsTail]):-

    cols(QueensTail,ColsTail).

    

diags1([],[]).

diags1([(Row,Col)|QueensTail],[Diagonal|DiagonalsTail]):-

    Diagonal is Col - Row,

    diags1(QueensTail,DiagonalsTail).

    

diags2([],[]).

diags2([(Row,Col)|QueensTail],[Diagonal|DiagonalsTail]):-

    Diagonal is Col + Row,

    diags2(QueensTail,DiagonalsTail).



eight_queens(Board) :-

    Board = [(1,_),(2,_),(3,_),(4,_),(5,_),(6,_),(7,_),(8,_)],

    length(Board,8),

    valid_board(Board),

    

    cols(Board,Cols),

    diags1(Board,Diags1),

    diags2(Board,Diags2),

    

    fd_all_different(Cols),

    fd_all_different(Diags1),

    fd_all_different(Diags2).

    

然后这样问问题：

eight_queens([(1,Y1),(2,Y2),(3,Y3),(4,Y4),(5,Y5),(6,Y6),(7,Y7),(8,Y8)]).

| ?- eight_queens([(1,Y1),(2,Y2),(3,Y3),(4,Y4),(5,Y5),(6,Y6),(7,Y7),(8,Y8)]).



Y1 = 1

Y2 = 5

Y3 = 8

Y4 = 6

Y5 = 3

Y6 = 7

Y7 = 2

Y8 = 4 ? a



Y1 = 1

Y2 = 6



Y1 = 2

Y2 = 7

Y3 = 3

Y4 = 6

Y5 = 8

Y7 = 6

Y8 = 3



Y1 = 2

Y2 = 8

Y3 = 6

Y4 = 1

Y5 = 3

Y6 = 5

Y7 = 7

Y8 = 4



Y1 = 3

Y2 = 1

Y3 = 7

Y4 = 5

Y5 = 8

Y6 = 2

Y7 = 4

Y8 = 6

……

Y1 = 8

Y2 = 3

Y3 = 1

Y4 = 6

Y5 = 2

Y6 = 5

Y7 = 7

Y8 = 4



Y1 = 8

Y2 = 4

Y3 = 1

Y4 = 3

Y5 = 6

Y6 = 2

Y7 = 7

Y8 = 5



(81860 ms) no

?后跟a可以一次性询问所有答案，可以看到还是相当的慢，这也算是声明式语言的一个劣势吧。

 

好了，今天介绍的两个问题就到此结束了。问题本身并不是重点，重点是我们思考问题的方式。 

最后提供：源代码下载，希望大家可以喜欢Prolog这门小巧简单，功能强大的语言。