用Path来绘制一些图形
Path是android中用来封装几何学路径的一个类,因为Path在图形绘制上占的比重还是相当大的。你可以用它来绘制各种样式的几何图形,做图表什么的都可以。
一、画线段
1.1 lineT(float x, float y)
先来看一段代码:
@Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); mPaint.setColor(Color.RED); mPaint.setStyle(Paint.Style.STROKE); mPaint.setStrokeWidth(5); // 实例化路径 mPath = new Path(); // 连接路径到点[100,100] mPath.lineTo(100, 100); // 绘制路径 canvas.drawPath(mPath, mPaint); }
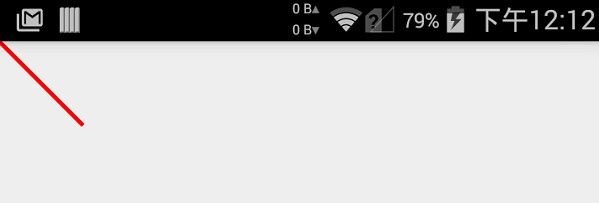
效果就是将起始点和(100,100)进行连接。这里因为没有设置起始点,所以默认是canvas的左上角,而这里默认的canvas和屏幕重合,所以就成了这个样子。
当然我们可以考虑多次调用lineTo方法来绘制更复杂的图形:
@Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); mPaint.setColor(Color.RED); mPaint.setStyle(Paint.Style.STROKE); mPaint.setStrokeWidth(5); // 实例化路径 mPath = new Path(); mPath.moveTo(100, 100); // 连接路径到点 mPath.lineTo(300, 100); mPath.lineTo(400, 200); mPath.lineTo(200, 200); // 绘制路径 canvas.drawPath(mPath, mPaint); }
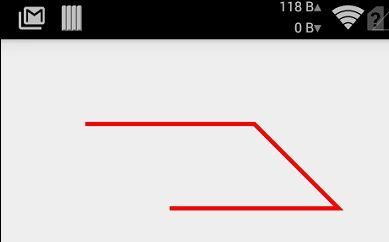
1.2 moveTo(float x, float y)
我们可以通过moveTo(float x, float y) 来移动起始的坐标点,比如:
@Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); mPaint.setColor(Color.RED); mPaint.setStyle(Paint.Style.STROKE); mPaint.setStrokeWidth(5); // 实例化路径 mPath = new Path(); //移动点至[300,300] mPath.moveTo(300, 300); // 连接路径到点[100,100] mPath.lineTo(100, 100); // 绘制路径 canvas.drawPath(mPath, mPaint); }
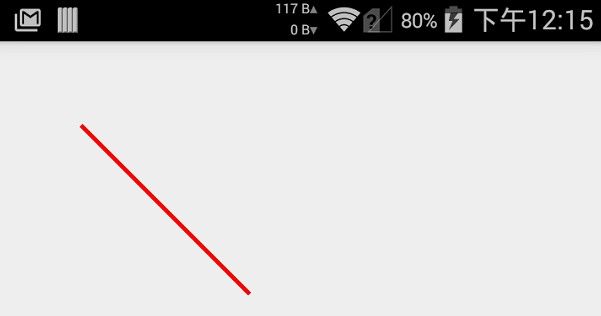
1.3 close()

上面的例子我们构建了一个类似平行四边形的图像,如果此时我们想闭合该曲线让它变成一个形状该怎么做呢?聪明的你一定想到:
mPath.lineTo(100, 100)
然而Path给我提供了更便捷的方法:
close()
在上面的例子添加close()后就会自动构建一条末点和起始点的线段:
@Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); mPaint.setColor(Color.RED); mPaint.setStyle(Paint.Style.STROKE); mPaint.setStrokeWidth(5); // 实例化路径 mPath = new Path(); mPath.moveTo(100, 100); // 连接路径到点 mPath.lineTo(300, 100); mPath.lineTo(400, 200); mPath.lineTo(200, 200); // 闭合曲线 mPath.close(); // 绘制路径 canvas.drawPath(mPath, mPaint); }
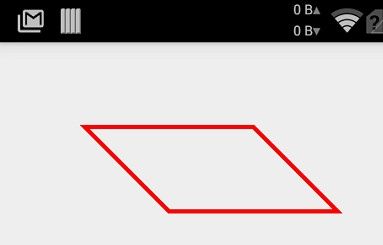
二、画贝赛尔曲线
2.1 贝赛尔曲线
什么叫贝赛尔曲线?其实很简单,使用三个或多个点来确定的一条曲线,贝塞尔曲线在图形图像学中有相当重要的地位,Path中也提供了一些方法来给我们模拟低阶贝赛尔曲线。
贝塞尔曲线的定义也比较简单,你只需要一个起点、一个终点和至少零个控制点则可定义一个贝赛尔曲线,当控制点为零时,只有起点和终点,此时的曲线说白了就是一条线段,我们称之为一阶贝赛尔曲线。
PS:以下图片和公式均来自维基百科和互联网
一阶贝赛尔曲线:
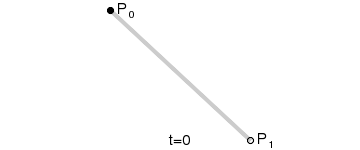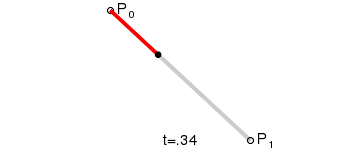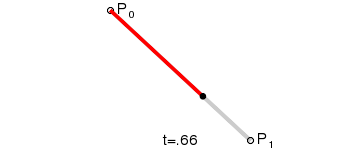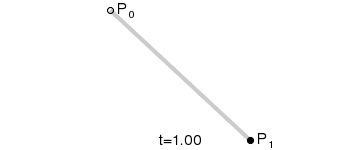
其公式可概括为:
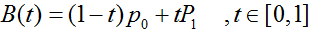
其中B(t)为时间为t时点的坐标,P0为起点、Pn为终点
贝塞尔曲线于1962年由法国数学家Pierre Bézier第一次研究使用并给出了详细的计算公式,So该曲线也是由其名字命名。Path中给出的quadTo方法属于
二阶贝赛尔曲线:
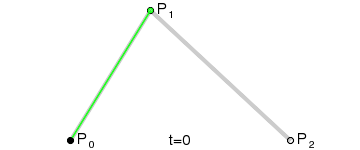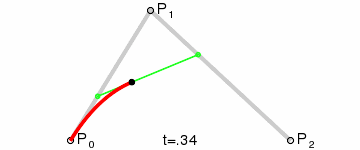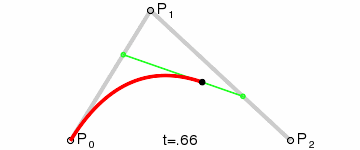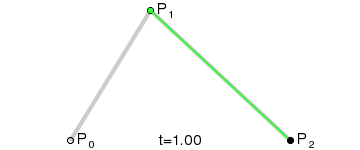
二阶贝赛尔曲线的一个明显特征是其拥有一个控制点,大家可以这样想想贝赛尔曲线,在一根两端固定橡皮筋上有一块磁铁,现在我们拿另一块磁铁去吸引橡皮筋上的磁铁,因为引力,橡皮筋会随着我们手上磁铁的移动而改变形状,又因为橡皮筋的张力让束缚在橡皮筋上的磁铁不会轻易吸附到我们手上的磁铁,这时橡皮筋的状态就可以看成是一条贝塞尔曲线,而我们手中的磁铁就是一个控制点,通过这个控制点我们“拉扯”橡皮筋的曲度。
二阶贝赛尔曲线的公式为:
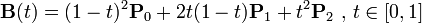
同样的,Path中也提供了三阶贝塞尔曲线的方法cubicTo,按照上面我们的推论,三阶应该是有两个控制点才对对吧
三阶贝赛尔曲线:
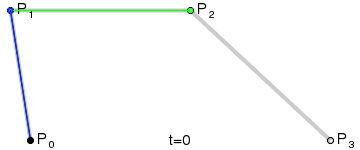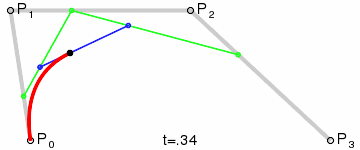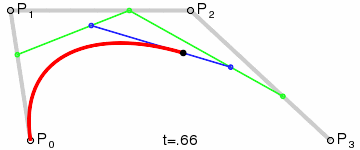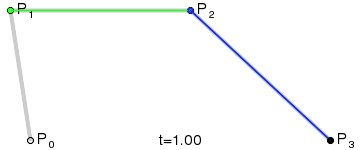
公式:
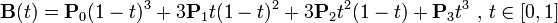
高阶贝赛尔曲线在Path中没有对应的方法,对我们来说三阶也足够了,不过大家可以了解下,难得我在墙外找到如此动感的贝赛尔曲线高清无码动图
高阶贝塞尔曲线:
四阶:
五阶:
贝塞尔曲线通用公式:
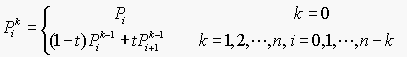
2.2 quadTo(float x1, float y1, float x2, float y2)
上面说了一阶的就是一条线段,所以直接来看二阶。下面的方法可以让我们绘制“二阶”贝赛尔曲线。
quadTo(float x1, float y1, float x2, float y2)

解释:其中quadTo的前两个参数为控制点的坐标,后两个参数为终点坐标,至于起点默认是画布的左上角。这里的p0就是起点,(x1,y1)就是中点P1,(x2,y2)就是末端点P2。
现在,我们使用它来绘制一条曲线:
@Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); mPaint.setColor(Color.RED); mPaint.setStyle(Paint.Style.STROKE); mPaint.setStrokeWidth(5); // 实例化路径 mPath = new Path(); // 移动起点至[100,100] mPath.moveTo(100, 100); // 连接路径到点 mPath.quadTo(200, 200, 300, 100); canvas.drawPath(mPath, mPaint); }
效果:
 示意图:
示意图: 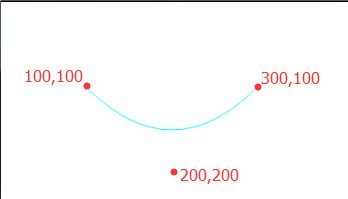
2.3 cubicTo(float x1, float y1, float x2, float y2, float x3, float y3)
它可以绘制三阶贝赛尔曲线。

与quadTo类似,前四个参数表示两个控制点,最后两个参数表示终点。其实,(x1,y1)就是P1,(x2,y2)是P2,(x3,y3)是P3。
下面用代码来绘制一下:
@Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); mPaint.setColor(Color.RED); mPaint.setStyle(Paint.Style.STROKE); mPaint.setStrokeWidth(5); // 实例化路径 mPath = new Path(); // 移动起点至[100,100] mPath.moveTo(100, 100); // 连接路径到点 mPath.cubicTo(200, 200, 300, 0, 400, 100); canvas.drawPath(mPath, mPaint); }
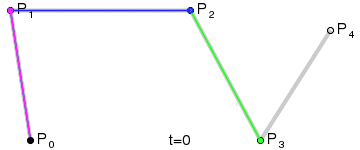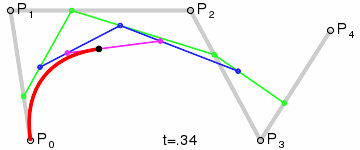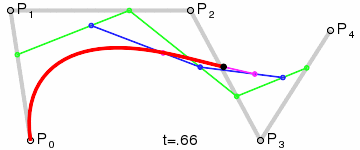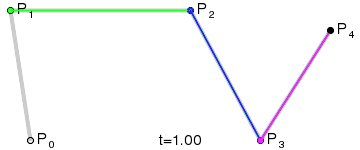
 示意图:
示意图: 
三、画弧线
arcTo (RectF oval, float startAngle, float sweepAngle)
是一个画弧线的方法,其实说白了就是从圆或椭圆上截取一部分而已。
@Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); mPaint.setColor(Color.RED); mPaint.setStyle(Paint.Style.STROKE); mPaint.setStrokeWidth(5); // 实例化路径 mPath = new Path(); // 移动起点至[100,100] mPath.moveTo(100, 100); // 连接路径到点 RectF oval = new RectF(100, 100, 200, 200); mPath.arcTo(oval, 0, 90); canvas.drawPath(mPath, mPaint); }
上面的代码首先构建出一个矩形区域,这个区域内就是椭圆和园的区域,椭圆或园会内切于这个矩形区域。然后我们设置圆弧的其实角度和最终角度来截取圆弧。

注意:使用Path生成的路径必定都是连贯的,虽然我们使用arcTo绘制的是一段弧但其最终都会与我们的起始点[100,100]连接。
如果你不想连怎么办?Path也提供了另一个重载方法:
arcTo (RectF oval, float startAngle, float sweepAngle, boolean forceMoveTo)
它会强制起点为绘制的起始点,而不是画布的左上角。我们来看看效果:
@Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); mPaint.setColor(Color.RED); mPaint.setStyle(Paint.Style.STROKE); mPaint.setStrokeWidth(5); // 实例化路径 mPath = new Path(); // 移动起点至[100,100] mPath.moveTo(100, 100); // 连接路径到点 RectF oval = new RectF(100, 100, 200, 200); mPath.arcTo(oval, 0, 90,true); canvas.drawPath(mPath, mPaint); }

四、rXXXTo方法
Path中除了上面介绍的几个XXXTo方法外还有一套rXXXTo方法:
rCubicTo(float x1, float y1, float x2, float y2, float x3, float y3) rLineTo(float dx, float dy) rMoveTo(float dx, float dy) rQuadTo(float dx1, float dy1, float dx2, float dy2)
这一系列rXXXTo方法其实跟上面的那些XXXTo差不多的,唯一的不同是rXXXTo方法的参考坐标是相对的而XXXTo方法的参考坐标始终是参照画布原点坐标,什么意思呢?举个简单的例子:
@Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); mPaint.setColor(Color.RED); mPaint.setStyle(Paint.Style.STROKE); mPaint.setStrokeWidth(5); // 实例化路径 mPath = new Path(); // 移动点至[100,100] mPath.moveTo(100, 100); // 连接路径到点 mPath.lineTo(200, 200); canvas.drawPath(mPath, mPaint); }
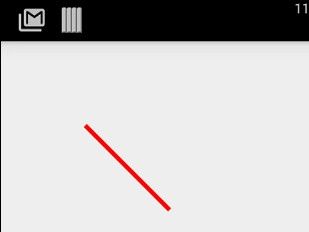
这里的move和lineTo的坐标都是对于画布左上角(0,0)来说的,是一个绝对坐标。而我们换为mPath.rLineTo(200, 200); 后呢?
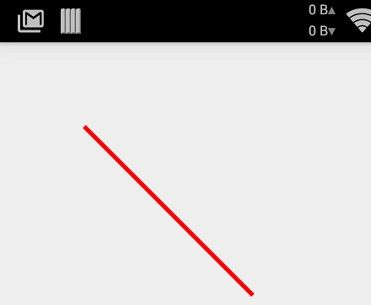
是不是感觉线段长了很多,因为这里的(200,200)是相对于开始点(100,100)来说的,是相对坐标。如果换算成绝对坐标就是绘制一条(100,100)到(300,300)之间的线段。其实,这个前缀“r”也就是relative(相对)的简写!
五、addXXX方法
XXXTo方法可以连接Path中的曲线而Path提供的另一系列addXXX方法则可以让我们直接往Path中添加一些曲线,比如
addArc(RectF oval, float startAngle, float sweepAngle)
它允许我们将一段弧形添加至Path,注意这里我用到了“添加”这个词汇,也就是说,通过addXXX方法添加到Path中的曲线是不会和上一次的曲线进行连接的:
@Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); mPaint.setColor(Color.RED); mPaint.setStyle(Paint.Style.STROKE); mPaint.setStrokeWidth(5); // 实例化路径 mPath = new Path(); // 移动点至[100,100] mPath.moveTo(100, 100); // 连接路径到点 mPath.lineTo(200, 200); // 添加一条弧线到Path中 RectF oval = new RectF(100, 100, 300, 400); mPath.addArc(oval, 0, 90); canvas.drawPath(mPath, mPaint); }

如图和代码所示,虽然我们先绘制了由[100,100]到[200,200]的线段,但是在我们往Path中添加了一条弧线后该弧线并没与线段连接。
除了addArc,Path还提供了一系列的add方法:
addCircle(float x, float y, float radius, Path.Direction dir) addOval(float left, float top, float right, float bottom, Path.Direction dir) addRect(float left, float top, float right, float bottom, Path.Direction dir) addRoundRect(float left, float top, float right, float bottom, float rx, float ry, Path.Direction dir)
这些方法和addArc有很明显的区别,就是多了一个Path.Direction参数,其他呢都大同小异,除此之外不知道大家还发现没有,addArc是往Path中添加一段弧,说白了就是一条开放的曲线,而上述几种方法都是一个具体的图形,或者说是一条闭合的曲线,Path.Direction的意思就是标识这些闭合曲线的闭合方向。Path.Direction只有两个常量值CCW和CW分别表示逆时针方向闭合和顺时针方向闭合。
那什么叫闭合方向呢?光说大家一定会蒙,有学习激情的童鞋看到后肯定会马上敲代码试验一下两者的区别,可是不管你如何改,单独地在一条闭合曲线上你是看不出所谓闭合方向的区别的。为了弄懂它,我们在path上绘制一些文字来说明最后参数的意义:
@Override protected void onDraw(Canvas canvas) { super.onDraw(canvas); mPaint.setColor(Color.RED); mPaint.setStyle(Paint.Style.STROKE); // 实例化路径 mPath = new Path(); // 移动起点至[100,100] mPath.moveTo(100, 100); // 添加一条弧线到Path中 RectF oval = new RectF(100, 100, 300, 400); mPath.addOval(oval, Path.Direction.CW); canvas.drawPath(mPath, mPaint); mPaint.setTextSize(50); // 绘制路径上的文字 canvas.drawTextOnPath("123456789", mPath, 0, 0, mPaint); }

如果我们换作:
mPath.addOval(oval, Path.Direction.CCW);

绘制的文字全都沿着Path跑到闭合曲线的“内部”了。
文章中大部分内容参考自:http://blog.csdn.net/aigestudio/article/details/41960507,本人对原文有少量的删减。本文记录在此,仅供学习之用,感谢原作者分享。
From AigeStudio(http://blog.csdn.net/aigestudio)Power by Aige ,感谢原作者。