背包九讲-01背包

tianyi cui 的背包九讲老版本：http://love-oriented.com/pack/，

更新后的版本PDF下载：http://cuitianyi.com/blog/%E3%80%8A%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E4%B9%9D%E8%AE%B2%E3%80%8B2-0-alpha1/

新版pdf下载地址2：http://download.csdn.net/detail/tangzhangpeng/5591321

本文实现了新版本第一章 “01背包问题”，代码中的注释也是针对新版本。

pdf 1.5 小节中的小错误，常数优化应该是

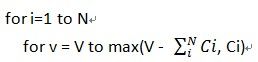，对Ci求和而不是对Wi求和

对1.5常数优化的解释：前 i  个物品获得的空间最小值是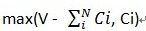：，即后面i~N个物品装满后剩余的空间，若剩余空间小于Ci，则为Ci

算法测试数据来自：http://www.cnblogs.com/jisi5789/archive/2013/04/11/3015745.html

相关代码如下：

  1 #include<iostream>

  2 #include<string>

  3 #include<vector>

  4 using namespace std;

  5 

  6 inline int max(int a, int b)

  7 {

  8     return a>b?a:b;

  9 }

 10 

 11 int ZeroOnePack1(int n, int v, int c[], int w[], bool needFull)

 12 {

 13     //根据tianyi cui背包九讲1.2的最原始的解法

 14     //时间空间复杂度均为O(nv)

 15     // n 物品数量

 16     // v 背包容量

 17     // c[] 物品耗费的空间,从c[1]开始

 18     // w[] 物品的价值，从w[1]开始

 19     // needFull 背包是否需要完全装满

 20     const int MIN = numeric_limits<int>::min(); //表示负无穷

 21     int **f = new int*[n+1];

 22     for(int i = 0; i < n+1; i++)

 23         f[i] = new int[v+1];

 24     if(needFull)  //初始化细节详见 背包九讲1.4

 25     {

 26         for(int i = 0; i <= n; i++)

 27             for(int j = 0; j <= v; j++)

 28                 f[i][j] = MIN;

 29         f[0][0] = 0;

 30     }

 31     else 

 32     {

 33         for(int i = 0; i <= n; i++)

 34             for(int j = 0; j <= v; j++)

 35                 f[i][j] = 0;

 36     }

 37     

 38     for(int i = 1; i <= n; i++)

 39         for(int j = c[i]; j <= v; j++)

 40         { 

 41             f[i][j] = max(f[i - 1][j], f[i - 1][j - c[i]] + w[i]);

 42         }

 43     if(f[n][v] < 0)return -1;  //针对背包装满的情况，没有满足的答案

 44     return f[n][v];

 45 }

 46 

 47 int ZeroOnePack2(int n, int v, int c[], int w[], bool needFull)

 48 {

 49     //根据tianyi cui背包九讲1.3在1.2的基础上优化空间复杂度后的解法

 50     //时间复杂度均为O(nv),空间复杂度为O(v)

 51     // n 物品数量

 52     // v 背包容量

 53     // c[] 物品耗费的空间,从c[1]开始

 54     // w[] 物品的价值，从w[1]开始

 55     // needFull 背包是否需要完全装满

 56     const int MIN = numeric_limits<int>::min(); //表示负无穷

 57     int *f = new int[v+1];

 58     if(needFull)  //初始化细节详见 背包九讲1.4

 59     {

 60         for(int i = 0; i <= v; i++)

 61             f[i] = MIN;

 62         f[0] = 0;

 63     }

 64     else 

 65     {

 66         for(int i = 0; i <= v; i++)

 67             f[i] = 0;

 68     }

 69     

 70     for(int i = 1; i <= n; i++)

 71         for(int j = v; j >= c[i]; j--)

 72         { 

 73             f[j] = max(f[j], f[j - c[i]] + w[i]);

 74         }

 75     if(f[v] < 0)return -1;  //针对背包装满的情况，没有满足的答案

 76     return f[v];

 77 }

 78 

 79 int ZeroOnePack3(int n, int v, int c[], int w[], bool needFull)

 80 {

 81     //根据tianyi cui背包九讲1.5,在1.3的基础上有个常数的优化，在v较大时，有明显优势

 82     //时间复杂度均为O(nv),空间复杂度为O(v)

 83     // n 物品数量

 84     // v 背包容量

 85     // c[] 物品耗费的空间,从c[1]开始

 86     // w[] 物品的价值，从w[1]开始

 87     // needFull 背包是否需要完全装满

 88     const int MIN = numeric_limits<int>::min(); //表示负无穷

 89     int *f = new int[v+1];

 90     if(needFull)  //初始化细节详见 背包九讲1.4

 91     {

 92         for(int i = 0; i <= v; i++)

 93             f[i] = MIN;

 94         f[0] = 0;

 95     }

 96     else 

 97     {

 98         for(int i = 0; i <= v; i++)

 99             f[i] = 0;

100     }

101     

102     int csum = 0;

103     c[0] = 0;

104     for(int i = 1; i <= n; i++)csum += c[i];

105     for(int i = 1; i <= n; i++)

106     {

107         csum -= c[i-1];

108         for(int j = v; j >= max(c[i], v - csum); j--)

109         { 

110             f[j] = max(f[j], f[j - c[i]] + w[i]);

111         }

112     }

113     if(f[v] < 0)return -1;  //针对背包装满的情况，没有满足的答案

114     return f[v];

115 }

116 

117 int main()

118 {

119     //87

120     int c[] = {0,2,7,3,4,8,5,8,6,4,16};

121     int w[] = {0,15,25,8,9,15,9,13,9,6,14};

122     int result = ZeroOnePack3(10, 34, c, w, true);

123     cout<< result <<endl;

124     

125     //82

126     int c1[] = {0,4,5,7,2,8,3,6,1,10,9};

127     int w1[] = {0,25,14,15,4,14,5,8,1,10,2};

128     int result1 = ZeroOnePack3(10, 34, c1, w1, true);

129     cout<< result1 <<endl;

130     

131     //-1

132     int c2[] = {0,2,3,6};

133     int w2[] = {0,15,10,16};

134     int result2 = ZeroOnePack3(3, 10, c2, w2, true);

135     cout<< result2 <<endl;

136     

137     //85

138     int c3[] = {0,2,8,4,4,8,7,8,5,16,16};

139     int w3[] = {0,15,25,9,9,15,12,12,6,14,9};

140     int result3 = ZeroOnePack3(10, 34, c3, w3, true);

141     cout<< result3 <<endl;

142     

143     //83

144     int c4[] = {0,4,5,7,2,8,3,9,6,1,10};

145     int w4[] = {0,25,14,15,4,14,5,14,8,1,10};

146     int result4 = ZeroOnePack3(10, 34, c4, w4, true);

147     cout<< result4 <<endl;

148 }

View Code

 【版权声明】转载请注明出处 http://www.cnblogs.com/TenosDoIt/p/3139092.html