算法实践——改良的求解数独的暴力搜索法
先回顾之前的三篇文章
“算法实践——数独的基本解法”,介绍求解数独的基本的暴力搜索法
“跳跃的舞者,舞蹈链(Dancing Links)算法——求解精确覆盖问题”,网友huangfeidian介绍的求解数独的舞蹈链(Dancing Links)算法,这篇文章是介绍舞蹈链(Dancing Links)算法的。
“算法实践——舞蹈链(Dancing Links)算法求解数独”,该文介绍了用舞蹈链(Dancing Links)算法求解数独,并给出了暴力破解法和舞蹈链(Dancing Links)算法之间的时间和空间占用效率的对比。
撇开空间占用的效率不谈,在前文中有下面的时间效率的数据对比
暴力破解法的效率
数独一:0.114毫秒
数独二:0.238毫秒
数独三:15.706毫秒
数独的舞蹈链(Sudoku Dancing Links)算法的效率
数独一:1.31毫秒
数独二:2.81毫秒
数独三:5.56毫秒
数独的舞蹈链(Sudoku Dancing Links)算法在数独一和数独二上不占优势,但是在数独三上的时间效率领先不止一点点
那是为何呢?通过分析三个数独可知,在暴力破解法中,数独一没有缓存数据,一路唯一数单元格到底;数独二缓存了12步数据;数独三缓存了21步数据;
于是做了推测,数独的舞蹈链(Sudoku Dancing Links)算法在缓存上优势,但是在构造数独矩阵的时候耗费了大量的时间。数独的缓存越多,该算法就越有优势,直到时间效率完全超越暴力破解法
在前文中也提到,数独的舞蹈链(Sudoku Dancing Links)算法本质上也是暴力破解法,只是采用了独特的数据结构,使得效率提升。于是针对数独三,把暴力破解法和数独的舞蹈链(Sudoku Dancing Links)算法的求解的前十步贴出来比较一下
先把数独三贴出来
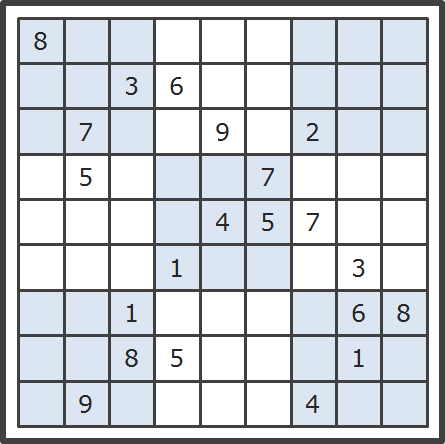
暴力破解法的前十步
1、缓存1,在(8,7)填数,2种可能(3或9)。先填3
2、缓存2,在(7,7)填数,2种可能(5或9)。先填5
3、缓存3,在(9,8)填数,2种可能(2或7)。先填2
4、在(9,9)填数,1种可能。填7
5、在(8,9)填数,1种可能。填9
6、缓存4,在(9,3)填数,2种可能(5或6)。先填6
7、缓存5,在(3,3)填数,2种可能(4或6)。先填6
8、缓存6,在(2,2)填数,2种可能(1或2)。先填1
9、缓存7,在(1,2)填数,2种可能(2或6)。先填2
10、缓存8,在(1,3)填数,2种可能(6或9)。先填6
可以看出暴力破解法的前十步中,有八步是缓存数据(每一步都有2种可能)。
数独的舞蹈链(Sudoku Dancing Links)算法的前十步
1、缓存1,在(8,7)填数,2种可能(3或9)。先填3
2、缓存2,在(7,7)填数,2种可能(5或9)。先填5
3、第6行填5,1种可能(在第9列),在(6,9)填5
4、第9宫填9,1种可能(在第8行、第9列),在(8,9)填9
5、缓存3,在(9,8)填数,2种可能(2或7)。先填2
6、在(9,9)填数,1种可能。填7
7、第3列填7,1种可能(在第6行),在(6,3)填7
8、缓存4,在(2,9)填数,2种可能(1或4)。先填1
9、第7列填1,1种可能(在第4行),在(4,7)填1
10、缓存5,在(1,7)填数,2种可能(6或9)。先填6
和暴力破解法的前十步相比,缓存数据的步数减少(有五步),增加了对行、列、宫填数的唯一性的判断。
例如:第3步中,当时第6行中能填5的格子,只有(6,9),虽然(6,9)中能填的数是2、4、5、6、9这5个数。那么只能在(6,9)中填5。减少了后续的计算可能。同理,第4步、第7步、第9步也是同样的道理
从这点看,由于数独的舞蹈链(Sudoku Dancing Links)算法增加了对行、列、宫填数的唯一性的判断,使得总步数大大减少,从而提高了时间效率。
那为何数独一和数独二不占时间优势呢?数独一一路唯一数单元格到底,不需要对行、列、宫填数的唯一性的判断。数独二,缓存的步数比较少,对行、列、宫填数的唯一性的判断虽然能减少步数,但可能不明显,加上其在构造数独矩阵上耗费了时间,所以总的时间损耗比较大,也就不占优势了。
那如果在暴力破解法中,增加对行、列、宫填数的唯一性的判断。是不是能提高求解的效率呢?
先增加下面的一个函数,对行、列、宫填数的唯一性的判断,如果有满足条件的唯一数,则返回坐标和数(组合,坐标*10+数),否则返回-1,其中P(K) = IIf(P(K) = -1, I * 9 + J, -2)是个条件判断,当P(K)=-1时,说明之前没有满足的条件,把P(K)设置成坐标值;当P(K)=-1时,说明之前有满足的条件,把P(K)设置成-2。然后一个循环判断P(K)值有没有大于-1(大于等于0)的,有说明有唯一数,返回坐标和数
Private Function GetOnly() As Integer
Dim I As Integer, J As Integer, K As Integer
Dim P(8) As Integer
'row
For I = 0 To 8
For K = 0 To 8
P(K) = -1
Next
For J = 0 To 8
If _Num(I * 9 + J) > 0 Then
For K = 0 To 8
If (_Num(I * 9 + J) And _V(K)) = _V(K) Then
P(K) = IIf(P(K) = -1, I * 9 + J, -2)
End If
Next
End If
Next
For K = 0 To 8
If P(K) >= 0 Then Return P(K) * 10 + K
Next
Next
'col
For I = 0 To 8
For K = 0 To 8
P(K) = -1
Next
For J = 0 To 8
If _Num(J * 9 + I) > 0 Then
For K = 0 To 8
If (_Num(J * 9 + I) And _V(K)) = _V(K) Then
P(K) = IIf(P(K) = -1, J * 9 + I, -2)
End If
Next
End If
Next
For K = 0 To 8
If P(K) >= 0 Then Return P(K) * 10 + K
Next
Next
'mat
Dim S As Integer
For I = 0 To 8
For K = 0 To 8
P(K) = -1
Next
For J = 0 To 8
S = (Int(I / 3) * 3 + Int(J / 3)) * 9 + (I Mod 3) * 3 + (J Mod 3)
If _Num(S) > 0 Then
For K = 0 To 8
If (_Num(S) And _V(K)) = _V(K) Then
P(K) = IIf(P(K) = -1, S, -2)
End If
Next
End If
Next
For K = 0 To 8
If P(K) >= 0 Then Return P(K) * 10 + K
Next
Next
Return -1
End Function
然后在FindMinCell函数中增加对行、列、宫填数的唯一性的判断,下面代码中红色的部分。但tP不等于-1时,说明此时没有唯一数单元格,那么判断有没有行、列、宫的唯一数。若有,则填数,并继续找寻唯一数单元格等;若没有,返回可选数最少的单元格
Private Function FindMinCell() As Integer
Dim I As Integer, C As Integer
Dim tP As Integer = -1, tMin As Integer = 20
I = 0
Dim S As Integer
Do
Do
If _Num(I) > 0 Then
C = Get1Count(_Num(I))
If C = 1 Then
If SetNumPri(I, _Num(I)) = False Then Return -2
If I = tP Then
tP = -1
tMin = 20
End If
I = -1
Else
If C < tMin Then
tP = I
tMin = C
End If
End If
End If
I += 1
Loop Until I > 80
If tP = -1 Then Return -1
S = GetOnly()
If S > 0 Then
Dim S2 As Integer = Int(S / 10)
Dim S3 As Integer = S Mod 10
If SetNumPri(S2, _V(S3)) = False Then Return -2
I = 0
tP = -1
tMin = 20
End If
Loop Until I > 80
Return tP
End Function
我把它称之为改良的暴力破解法,下面看看三个算法对求解数独的时间效率的对比(从新测定,数据和之前的有偏差,和电脑运行时状态有关)
暴力破解法
数独一:0.113毫秒
数独二:0.240毫秒
数独三:15.555毫秒
数独的舞蹈链(Sudoku Dancing Links)算法
数独一:6.323毫秒
数独二:8.484毫秒
数独三:11.239毫秒
改良的暴力破解法
数独一:0.113毫秒
数独二:0.837毫秒
数独三:11.324毫秒
从上面的数据可以看出,改良的暴力破解法在数独一和数独三上基本上都到了三者最优的状态。在数独二上没有体现优势,推测问题出在数独二上行、列、宫的唯一数可能性比较少,但为此耗费了不少的计算时间。
把改良的暴力破解法和暴力破解法的求解数独三过程保存到文件分析了一下,改良的暴力破解法的文件的大小是暴力破解法的20%左右,说明改良的暴力破解法大大缩小了求解的步数,也就是提高了求解的时间效率。
还能不能改良?在本文中,在没有唯一数单元格时,再求解行、列、宫的唯一数的过程,那么这里面有很多的重复计算。能不能在每次填数的时候,都把行、列、宫的可填性更新,这样在求解行、列、宫的唯一数的过程中就不需要重新计算了。我试了一下,一是空间占用成本高,需要额外的243字节存储行、列、宫的可填性,每次缓存的时候,这243字节也要缓存,增加缓存的负担。二是每次填数的时候,更新行、列、宫的可填性的计算比较复杂,需要耗费比较多的计算时间。三是在数独一和数独二的情况下,对行、列、宫的可填性依赖不大,更新行、列、宫的可填性的计算反而是做了很多的无用功(尤其是数独一,根本不需要对行、列、宫的可填性的判断),耗费计算时间,降低时间效率。
如果网友中还有什么其他比较好的数独的求解方法,望不吝赐教,大家互相交流,共同提高。