机器学习浅析之最优解问题（二）

本文主要讨论了机器学习中的最大似然估计MLE，贝叶斯估计和最大后验估计MAP，以及它们的关系，是上一篇《机器学习浅析之最优解问题》的深入。

最大似然估计MLE

Frequentist Learning假定存在模型M，其中未知参数为.该参数的估计值为. 给定样本观察数据X，通过选择合适的θ值，可以使产生该样本数据X的概率最大。

首先介绍逆概率公式：

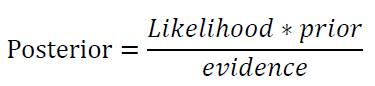
即

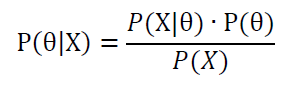
它可以将后验概率转化为给予先验概率和似然函数的表达式，所以最大似然估计MLE就是要用似然函数取得最大值时的参数值作为估计值。

MLE的过程如下：

首先，写出样本观察数据的联合分布的表达式：

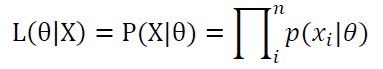
其次，取对数可得：

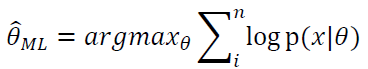
最后，这是一个关于θ的函数，求导可得极值点，取最大值时对应的θ取值就是合适的模型参数。

以抛硬币为例，单次试验服从伯努利分布，N次试验服从二项分布，模型参数为θ，即每次得到正面的概率为θ。为了估计该参数，采用最大似然估计：

似然函数的对数为：

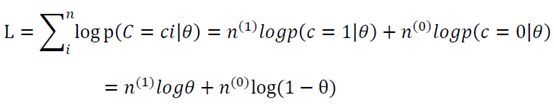
求导可得

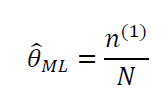
最大似然估计中，参数θ是一个固定的值，只要能够拟合样本数据就可以了。但是当样本过少的时候就容易出现过拟合现象，会得到诸如只要没见过飞机相撞，飞机就一定不会相撞的扭曲事实。

 

最大后验估计MAP

最大后验估计与最大似然估计相似，不同点在于需要考虑先验概率p(θ)。也就是说，此时不是要去求似然函数取得最大值，而是要去求贝叶斯公式计算出的整个后验概率最大值时的θ。

即

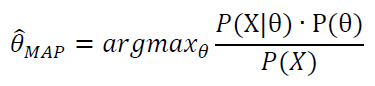
这里的P(X)与θ无关，因此等价于使分子最大即可。

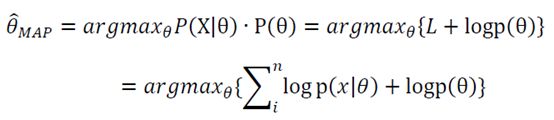
此处的先验概率p(θ)可以用来描述人们已知的普遍规律，例如在扔硬币试验中，每次抛出正面的概率θ应该服从一个概率分布，且在θ=0.5时取得最大值。该分布就是先验分布，其参数称为超参数。即p(θ)=p(θ|α)

同理，上述后验概率取得最大值时，可得MAP估计出的参数值。

仍以抛硬币为例，假设硬币均匀，先验概率分布在θ=0.5时取得最大值。选用beta分布作为θ的分布，即θ~Beta(α,β)，当α,β=5时，p(θ=0.5)，由上面公式推导可得：

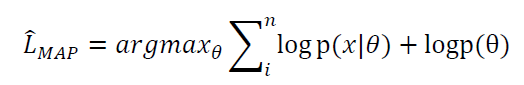
其中

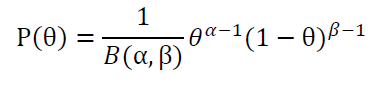
求导可得参数θ的最大估计值

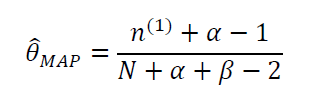
从中我们可以看出先验概率的作用为

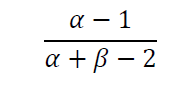
例如，当我们做商品个性化推荐的时候，当无法获得用户个人喜好的时候，只好根据先验概率推荐大众热门的商品给他。

贝叶斯估计Bayesian learning

贝叶斯估计是在MAP上的进一步扩展，此时不再是直接估计参数值，而是允许参数服从一定的分布。所以现在不是要求后验概率最大时的参数值。

根据

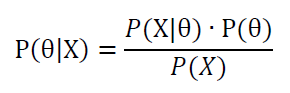
其中,根据全概率公式：

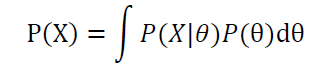
当新的数据被观察到时，后验概率可以随之调整。

预测方法如下：

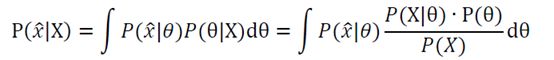
以抛硬币为例，和MAP中一样，假设先验分布为beta分布，但是在构造贝叶斯估计的时候，不是要用最大后验概率时的参数来近似作为参数值，而是求满足beta分布的参数的期望。

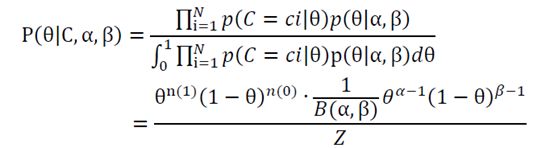
因为在Beta分布中

所以

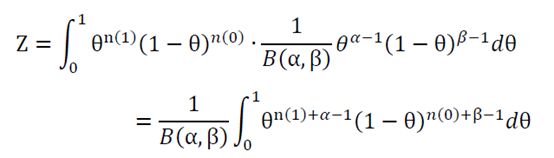
于是可得

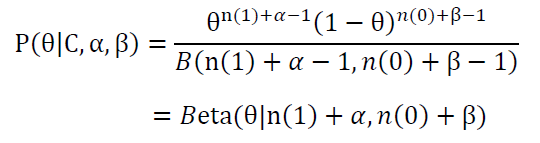
根据结果可知，根据贝叶斯估计，参数θ服从一个新的beta分布。

在MAP中，我们为θ选取的先验分布为beta分布，后来以θ参数的二项分布用贝叶斯估计得到的θ的后验概率仍服从beta分布，由此可知二项分布与beta分布为共轭分布。

当随机变量取值为二维时，可以使用beta分布来处理，而多维时可以使用狄利克雷分布。在概率语言模型中，通常选取共轭分布为先验分布，从而带来计算的方便性。LDA中每个文档的topic服从多项式分布，其先验分布选取狄利克雷分布。

由于在贝叶斯估计中，参数的后验概率是比较难以计算的，因为要对所有的参数进行积分，而且，这个积分其实就是所有θ的后验概率的汇总，其实它是与最优θ是无关的，而我们只关心最优θ（p(x)相同）。在这种情况下，我们采用了一种近似的方法求后验概率，这就是最大后验估计：

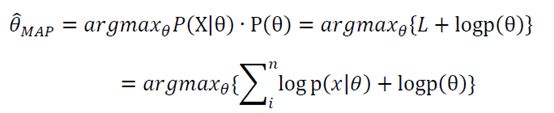
最大后验估计相比最大似然估计，只是多了一项先验概率，它正好体现了贝叶斯认为参数也是随机变量的观点，在实际运算中通常通过超参数给出先验分布。最大似然估计其实是经验风险最小化的一个例子，而最大后验估计是结构风险最小化的一个例子。如果样本数据足够大，最大后验概率和最大似然估计趋向于一致，如果样本数据为0，最大后验就仅由先验概率决定。尽管最大后验估计看着要比最大似然估计完善，但是由于最大似然估计简单，很多方法还是使用最大似然估计。