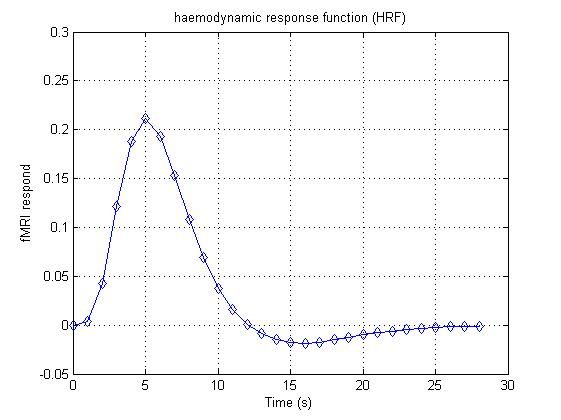
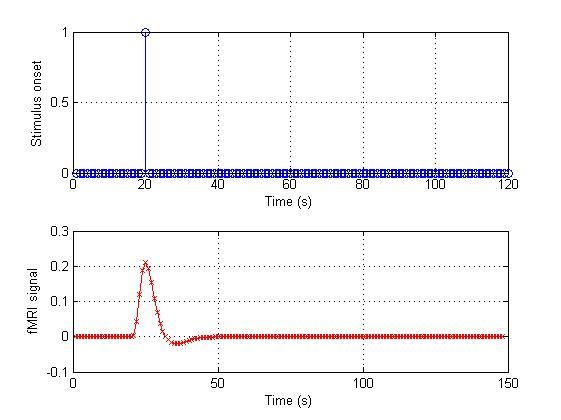
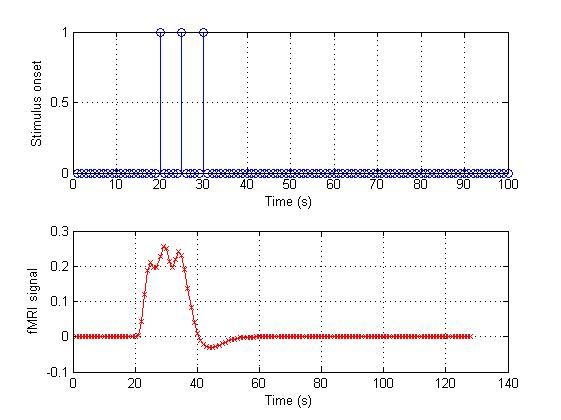
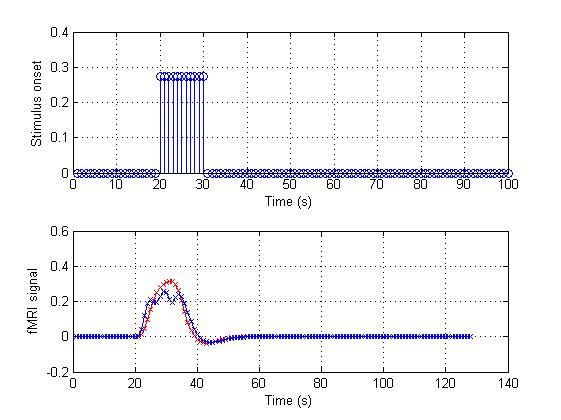
一、什么是宏函数?通过宏定义的函数是宏函数。如下,编译器在预处理阶段会将Add(x,y)替换为((x)*(y))#defineAdd(x,y)((x)*(y))#defineAdd(x,y)((x)*(y))intmain(){inta=10;intb=20;intd=10;intc=Add(a+d,b)*2;cout<
C语言如何定义宏函数?
小九格物
c语言
在C语言中,宏函数是通过预处理器定义的,它在编译之前替换代码中的宏调用。宏函数可以模拟函数的行为,但它们不是真正的函数,因为它们在编译时不会进行类型检查,也不会分配存储空间。宏函数的定义通常使用#define指令,后面跟着宏的名称和参数列表,以及宏展开后的代码。宏函数的定义方式:1.基本宏函数:这是最简单的宏函数形式,它直接定义一个表达式。#defineSQUARE(x)((x)*(x))2.带参
【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数
广龙宇
一起学Rust#Rust设计模式rust设计模式开发语言
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言,它的所有特性,使其独一无二。因此,学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此,本系列文章的结构也与此书的结构相同(后续可能会调成结构),基本上分为三个部分
每日一题——第八十四题
互联网打工人no1
C语言程序设计每日一练c语言
题目:编写函数1、输入10个职工的姓名和职工号2、按照职工由大到小顺序排列,姓名顺序也随之调整3、要求输入一个职工号,用折半查找法找出该职工的姓名#define_CRT_SECURE_NO_WARNINGS#include#include#defineMAX_EMPLOYEES10typedefstruct{intid;charname[50];}Empolyee;voidinputEmploye
Python教程:一文了解使用Python处理XPath
旦莫
Python进阶python开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath?2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
Day17笔记-高阶函数
~在杰难逃~
Python笔记python开发语言pycharm数据分析
高阶函数【重点掌握】函数的本质:函数是一个变量,函数名是一个变量名,一个函数可以作为另一个函数的参数或返回值使用如果A函数作为B函数的参数,B函数调用完成之后,会得到一个结果,则B函数被称为高阶函数常用的高阶函数:map(),reduce(),filter(),sorted()1.map()map(func,iterable),返回值是一个iterator【容器,迭代器】func:函数iterab
Python快速入门 —— 第三节:类与对象
孤华暗香
Python快速入门python开发语言
第三节:类与对象目标:了解面向对象编程的基础概念,并学会如何定义类和创建对象。内容:类与对象:定义类:class关键字。类的构造函数:__init__()。类的属性和方法。对象的创建与使用。示例:classStudent:def__init__(self,name,age,major):self.name&#
Python爬虫解析工具之xpath使用详解
eqa11
python爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中,数据提取是一个至关重要的环节。xpath作为一门
ARM驱动学习之5 LEDS驱动
JT灬新一
嵌入式C底层arm开发学习单片机
ARM驱动学习之5LEDS驱动知识点:•linuxGPIO申请函数和赋值函数–gpio_request–gpio_set_value•三星平台配置GPIO函数–s3c_gpio_cfgpin•GPIO配置输出模式的宏变量–S3C_GPIO_OUTPUT注意点:DRIVER_NAME和DEVICE_NAME匹配。实现步骤:1.加入需要的头文件://Linux平台的gpio头文件#include//三
Rust基础知识
GRKF15
rust开发语言后端
1.Rust语言简介1.1基础语法变量声明:let关键字用于声明变量,可以指定或不指定类型,如leta=10;和letmutc=30i32;。函数定义:使用fn关键字定义函数,并指定参数类型及返回类型,如fnadd(i:i32,j:i32)->i32{i+j}。控制流:包括if、else等,控制语句后需要使用;来结束语句。1.2数据类型整数类型:i8、i16、i32、i64、i128,以及无符号的
STM32中的计时与延时
lupinjia
STM32stm32单片机
前言在裸机开发中,延时作为一种规定循环周期的方式经常被使用,其中尤以HAL库官方提供的HAL_Delay为甚。刚入门的小白可能会觉得既然有官方提供的延时函数,而且精度也还挺好,为什么不用呢?实际上HAL_Delay中有不少坑,而这些也只是HAL库中无数坑的其中一些。想从坑里跳出来还是得加强外设原理的学习和理解,切不可只依赖HAL库。除了延时之外,我们在开发中有时也会想要确定某段程序的耗时,这就需要
python多线程程序设计 之一
IT_Beijing_BIT
#Python程序设计语言python
python多线程程序设计之一全局解释器锁线程APIsthreading.active_count()threading.current_thread()threading.excepthook(args,/)threading.get_native_id()threading.main_thread()threading.stack_size([size])线程对象成员函数构造器start/ru
Android应用性能优化
轻口味
Android
Android手机由于其本身的后台机制和硬件特点,性能上一直被诟病,所以软件开发者对软件本身的性能优化就显得尤为重要;本文将对Android开发过程中性能优化的各个方面做一个回顾与总结。Cache优化ListView缓存:ListView中有一个回收器,Item滑出界面的时候View会回收到这里,需要显示新的Item的时候,就尽量重用回收器里面的View;每次在getView函数中inflate新
C++ lambda闭包消除类成员变量
barbyQAQ
c++c++java算法
原文链接:https://blog.csdn.net/qq_51470638/article/details/142151502一、背景在面向对象编程时,常常要添加类成员变量。然而类成员一旦多了之后,也会带来干扰。拿到一个类,一看成员变量好几十个,就问你怕不怕?二、解决思路可以借助函数式编程思想,来消除一些不必要的类成员变量。三、实例举个例子:classClassA{public:...intfu
C++八股
Petrichorzncu
八股总结c++开发语言
这里写目录标题C++内存管理C++的构造函数,复制构造函数,和析构函数深复制与浅复制:构造函数和析构函数哪个能写成虚函数,为什么?C++数据结构内存排列结构体和类占用的内存:==虚函数和虚表的原理==虚函数虚表(Vtable)虚函数和虚表的实现细节==内存泄漏==指针的工作原理函数的传值和传址new和delete与malloc和freeC++内存区域划分C++11新特性C++常见新特性==智能指针
【Python搞定车载自动化测试】——Python实现车载以太网DoIP刷写(含Python源码)
疯狂的机器人
Python搞定车载自动化pythonDoIPUDSISO142291SO13400Bootloadertcp/ip
系列文章目录【Python搞定车载自动化测试】系列文章目录汇总文章目录系列文章目录前言一、环境搭建1.软件环境2.硬件环境二、目录结构三、源码展示1.DoIP诊断基础函数方法2.DoIP诊断业务函数方法3.27服务安全解锁4.DoIP自动化刷写四、测试日志1.测试日志五、完整源码链接前言随着智能电动汽车行业的发展,汽车=智能终端+四个轮子,各家车企都推出了各自的OTA升级方案,本章节主要介绍如何使
【2022 CCF 非专业级别软件能力认证第一轮(CSP-J1)入门级 C++语言试题及解析】
汉子萌萌哒
CCFnoi算法数据结构c++
一、单项选择题(共15题,每题2分,共计30分;每题有且仅有一个正确选项)1.以下哪种功能没有涉及C++语言的面向对象特性支持:()。A.C++中调用printf函数B.C++中调用用户定义的类成员函数C.C++中构造一个class或structD.C++中构造来源于同一基类的多个派生类题目解析【解析】正确答案:AC++基础知识,面向对象和类有关,类又涉及父类、子类、继承、派生等关系,printf
matlab delsat = setdiff(1:69,unique(Eph(30,:))); 语句含义
黄卷青灯77
matlab开发语言setdiff
这行MATLAB代码用于计算在范围1:69中不包含在Eph矩阵第30行的唯一值集合中的所有元素。具体解释如下:delsat=setdiff(1:69,unique(Eph(30,:)));解释Eph(30,:)Eph(30,:)提取矩阵Eph的第30行的所有列元素。这是一个行向量,包含了第30行的所有值。unique(Eph(30,:))unique函数返回Eph(30,:)中的唯一元素。这意味着
【RabbitMQ 项目】服务端:数据管理模块之绑定管理
月夜星辉雪
rabbitmq分布式
文章目录一.编写思路二.代码实践一.编写思路定义绑定信息类交换机名称队列名称绑定关键字:交换机的路由交换算法中会用到没有是否持久化的标志,因为绑定是否持久化取决于交换机和队列是否持久化,只有它们都持久化时绑定才需要持久化。绑定就好像一根绳子,两端连接着交换机和队列,当一方不存在,它就没有存在的必要了定义绑定持久化类构造函数:如果数据库文件不存在则创建,打开数据库,创建binding_table插入
粒子群优化 (PSO) 在三维正弦波函数中的应用
subject625Ruben
机器学习人工智能matlab算法
在这篇博客中,我们将展示如何使用粒子群优化(PSO)算法求解三维正弦波函数,并通过增加正弦波扰动,使优化过程更加复杂和有趣。本文将介绍目标函数的定义、PSO参数设置以及算法执行的详细过程,并展示搜索空间中的动态过程和收敛曲线。1.目标函数定义我们使用的目标函数是一个三维正弦波函数,定义如下:objectiveFunc=@(x)sin(sqrt(x(1).^2+x(2).^2))+0.5*sin(5
c++ 内存处理函数
heeheeai
c++开发语言
在C语言的头文件中,memcpy和memmove函数都用于复制内存块,但它们在处理内存重叠方面存在关键区别:内存重叠:memcpy函数不保证在源内存和目标内存区域重叠时能够正确复制数据。如果内存区域重叠,memcpy的行为是未定义的,可能会导致数据损坏或程序崩溃。memmove函数能够安全地处理源内存和目标内存区域重叠的情况。它会确保在复制过程中不会覆盖尚未复制的数据,从而保证数据的完整性。效率:
Python编程 - 函数进阶
易辰君
Python核心编程python开发语言
目录前言一、函数参数的高级用法(一)缺省参数(二)命名参数(三)不定长参数二、拆包(一)函数返回值拆包(二)通过星号拆包(三)总结三、匿名函数(一)函数定义(二)使用匿名函数四、递归函数(一)简介(二)基本结构(三)简单示例(四)优缺点总结前言上篇文章主要了解了函数基础,如何定义函数,函数种类以及局部变量和全局变量的差异等,接下来就讲解python函数较为进阶的知识点,若有任何想法欢迎一起沟通讨论
Python编程 - 初识面向对象
易辰君
Python核心编程python开发语言
目录前言一、面向对象二、类和对象(一)类简介定义类(二)对象简介创建对象(三)总结三、实例属性和实例方法(一)实例属性创建的基本语法使用示例(二)实例方法定义实例方法的基本语法调用示例方法的示例(三)总结四、类中的self(一)基本概念(二)作用访问实例属性调用其他实例方法在构造函数中初始化对象(三)总结五、__init__方法(一)__init__方法的特点(二)基本语法(三)示例(四)总结前言
[实践应用] 深度学习之优化器
YuanDaima2048
深度学习工具使用pytorch深度学习人工智能机器学习python优化器
文章总览:YuanDaiMa2048博客文章总览深度学习之优化器1.随机梯度下降(SGD)2.动量优化(Momentum)3.自适应梯度(Adagrad)4.自适应矩估计(Adam)5.RMSprop总结其他介绍在深度学习中,优化器用于更新模型的参数,以最小化损失函数。常见的优化函数有很多种,下面是几种主流的优化器及其特点、原理和PyTorch实现:1.随机梯度下降(SGD)原理:随机梯度下降通过
Go语言基础总结
Alice_小哪吒
Go学习笔记golang开发语言后端
一、Go语言结构包声明引入包函数变量语句&表达式注释下面简单给出hello.go文件。packagesrc/*定义包名*/import"fmt"/*引入包*/funchello(){/*函数*/fmt.Println("Hello,World!")/*语句&表达式*/fmt.Println("菜鸟教程:runoob.com")}二、Go语言基础语法Go程序可以由多个标记构成。可以是关键字、标识符、
TC27x启动过程(2)-TC277
赞哥哥s
TC277学习笔记gnu单片机
接上文,继续学习TC277的启动过程。分析启动函数有关用的寄存器说明,参考文章TC27x寄存器学习目录TC27x寄存器学习start函数分析isync汇编指令(同步指令)dsync汇编指令(同步数据),1清除endinit2设置中断堆栈3启用对系统全局寄存器的写访问4初始化SDA基指针5关闭对系统全局寄存器的写访问6关闭看门狗,恢复Endinit位7初始化CSA8初始化ram,拷贝rom数据到ra
vue render 函数详解 (配参数详解)
你的眼睛會笑
vue2vue.jsjavascript前端
vuerender函数详解(配参数详解)在Vue3中,`render`函数被用来代替Vue2中的模板语法。它接收一个h函数(或者是`createElement`函数的别名),并且返回一个虚拟DOM。render函数的语法结构如下:render(h){returnh('div',{class:'container'},'Hello,World!')}在上面的示例中,我们使用h函数创建了一个div元素
python老是报参数未定义_Python函数默认参数常见问题及解决方案
weixin_39935571
python老是报参数未定义
一、默认参数python为了简化函数的调用,提供了默认参数机制:这样在调用pow函数时,就可以省略最后一个参数不写:在定义有默认参数的函数时,需要注意以下:必选参数必须在前面,默认参数在后;设置何种参数为默认参数?一般来说,将参数值变化小的设置为默认参数。python标准库实践python内建函数:函数签名可以看出,使用print('hellopython')这样的简单调用的打印语句,实际上传入了
3.1 损失函数和优化:损失函数
做只小考拉
用一个函数把W当做输入,然后看一下得分,定量地估计W的好坏,这个函数被称为“损失函数”。损失函数用于度量W的好坏。有了损失函数的概念后,就可以定量的衡量W到底是好还是坏,要找到一种有效的方法来从W的可行域里,找到W取何值时情况最不坏,,这个过程将会是一个优化过程。损失函数L_i定义:通过函数f给出预测的分数和真实的目标(或者说是标签y),可以定量的描述训练样本预测的好不好,最终的损失函数是在整个数
详解“c:/work/src/components/a/b.vue“‘ has no default export报错原因
hw_happy
开发语言前端vue.jsjavascript
前情提要在一个vue文件中需要引入定义的b.vue文件,但是提示b文件没有默认导出,对于vue2文件来说有exportdefault,在中,所有定义的变量、函数和组件都会自动被视为默认导出的组件内容。因此,不需要显式地使用exportdefault来导出组件。但是在我引用这个文件的时候还是提示了这个错误,原来是我的项目使用了ts和vite\webpack,因为TypeScript和Vue的默认导出
Linux的Initrd机制
被触发
linux
Linux 的 initrd 技术是一个非常普遍使用的机制,linux2.6 内核的 initrd 的文件格式由原来的文件系统镜像文件转变成了 cpio 格式,变化不仅反映在文件格式上, linux 内核对这两种格式的 initrd 的处理有着截然的不同。本文首先介绍了什么是 initrd 技术,然后分别介绍了 Linux2.4 内核和 2.6 内核的 initrd 的处理流程。最后通过对 Lin
maven本地仓库路径修改
bitcarter
maven
默认maven本地仓库路径:C:\Users\Administrator\.m2
修改maven本地仓库路径方法:
1.打开E:\maven\apache-maven-2.2.1\conf\settings.xml
2.找到
XSD和XML中的命名空间
darrenzhu
xmlxsdschemanamespace命名空间
http://www.360doc.com/content/12/0418/10/9437165_204585479.shtml
http://blog.csdn.net/wanghuan203/article/details/9203621
http://blog.csdn.net/wanghuan203/article/details/9204337
http://www.cn
Java 求素数运算
周凡杨
java算法素数
网络上对求素数之解数不胜数,我在此总结归纳一下,同时对一些编码,加以改进,效率有成倍热提高。
第一种:
原理: 6N(+-)1法 任何一个自然数,总可以表示成为如下的形式之一: 6N,6N+1,6N+2,6N+3,6N+4,6N+5 (N=0,1,2,…)
java 单例模式
g21121
java
想必单例模式大家都不会陌生,有如下两种方式来实现单例模式:
class Singleton {
private static Singleton instance=new Singleton();
private Singleton(){}
static Singleton getInstance() {
return instance;
}
Linux下Mysql源码安装
510888780
mysql
1.假设已经有mysql-5.6.23-linux-glibc2.5-x86_64.tar.gz
(1)创建mysql的安装目录及数据库存放目录
解压缩下载的源码包,目录结构,特殊指定的目录除外:
32位和64位操作系统
墙头上一根草
32位和64位操作系统
32位和64位操作系统是指:CPU一次处理数据的能力是32位还是64位。现在市场上的CPU一般都是64位的,但是这些CPU并不是真正意义上的64 位CPU,里面依然保留了大部分32位的技术,只是进行了部分64位的改进。32位和64位的区别还涉及了内存的寻址方面,32位系统的最大寻址空间是2 的32次方= 4294967296(bit)= 4(GB)左右,而64位系统的最大寻址空间的寻址空间则达到了
我的spring学习笔记10-轻量级_Spring框架
aijuans
Spring 3
一、问题提问:
→ 请简单介绍一下什么是轻量级?
轻量级(Leightweight)是相对于一些重量级的容器来说的,比如Spring的核心是一个轻量级的容器,Spring的核心包在文件容量上只有不到1M大小,使用Spring核心包所需要的资源也是很少的,您甚至可以在小型设备中使用Spring。
mongodb 环境搭建及简单CURD
antlove
WebInstallcurdNoSQLmongo
一 搭建mongodb环境
1. 在mongo官网下载mongodb
2. 在本地创建目录 "D:\Program Files\mongodb-win32-i386-2.6.4\data\db"
3. 运行mongodb服务 [mongod.exe --dbpath "D:\Program Files\mongodb-win32-i386-2.6.4\data\
数据字典和动态视图
百合不是茶
oracle数据字典动态视图系统和对象权限
数据字典(data dictionary)是 Oracle 数据库的一个重要组成部分,这是一组用于记录数据库信息的只读(read-only)表。随着数据库的启动而启动,数据库关闭时数据字典也关闭 数据字典中包含
数据库中所有方案对象(schema object)的定义(包括表,视图,索引,簇,同义词,序列,过程,函数,包,触发器等等)
数据库为一
多线程编程一般规则
bijian1013
javathread多线程java多线程
如果两个工两个以上的线程都修改一个对象,那么把执行修改的方法定义为被同步的,如果对象更新影响到只读方法,那么只读方法也要定义成同步的。
不要滥用同步。如果在一个对象内的不同的方法访问的不是同一个数据,就不要将方法设置为synchronized的。
将文件或目录拷贝到另一个Linux系统的命令scp
bijian1013
linuxunixscp
一.功能说明 scp就是security copy,用于将文件或者目录从一个Linux系统拷贝到另一个Linux系统下。scp传输数据用的是SSH协议,保证了数据传输的安全,其格式如下: scp 远程用户名@IP地址:文件的绝对路径
【持久化框架MyBatis3五】MyBatis3一对多关联查询
bit1129
Mybatis3
以教员和课程为例介绍一对多关联关系,在这里认为一个教员可以叫多门课程,而一门课程只有1个教员教,这种关系在实际中不太常见,通过教员和课程是多对多的关系。
示例数据:
地址表:
CREATE TABLE ADDRESSES
(
ADDR_ID INT(11) NOT NULL AUTO_INCREMENT,
STREET VAR
cookie状态判断引发的查找问题
bitcarter
formcgi
先说一下我们的业务背景:
1.前台将图片和文本通过form表单提交到后台,图片我们都做了base64的编码,并且前台图片进行了压缩
2.form中action是一个cgi服务
3.后台cgi服务同时供PC,H5,APP
4.后台cgi中调用公共的cookie状态判断方法(公共的,大家都用,几年了没有问题)
问题:(折腾两天。。。。)
1.PC端cgi服务正常调用,cookie判断没
通过Nginx,Tomcat访问日志(access log)记录请求耗时
ronin47
一、Nginx通过$upstream_response_time $request_time统计请求和后台服务响应时间
nginx.conf使用配置方式:
log_format main '$remote_addr - $remote_user [$time_local] "$request" ''$status $body_bytes_sent "$http_r
java-67- n个骰子的点数。 把n个骰子扔在地上,所有骰子朝上一面的点数之和为S。输入n,打印出S的所有可能的值出现的概率。
bylijinnan
java
public class ProbabilityOfDice {
/**
* Q67 n个骰子的点数
* 把n个骰子扔在地上,所有骰子朝上一面的点数之和为S。输入n,打印出S的所有可能的值出现的概率。
* 在以下求解过程中,我们把骰子看作是有序的。
* 例如当n=2时,我们认为(1,2)和(2,1)是两种不同的情况
*/
private stati
看别人的博客,觉得心情很好
Cb123456
博客心情
以为写博客,就是总结,就和日记一样吧,同时也在督促自己。今天看了好长时间博客:
职业规划:
http://www.iteye.com/blogs/subjects/zhiyeguihua
android学习:
1.http://byandby.i
[JWFD开源工作流]尝试用原生代码引擎实现循环反馈拓扑分析
comsci
工作流
我们已经不满足于仅仅跳跃一次,通过对引擎的升级,今天我测试了一下循环反馈模式,大概跑了200圈,引擎报一个溢出错误
在一个流程图的结束节点中嵌入一段方程,每次引擎运行到这个节点的时候,通过实时编译器GM模块,计算这个方程,计算结果与预设值进行比较,符合条件则跳跃到开始节点,继续新一轮拓扑分析,直到遇到
JS常用的事件及方法
cwqcwqmax9
js
事件 描述
onactivate 当对象设置为活动元素时触发。
onafterupdate 当成功更新数据源对象中的关联对象后在数据绑定对象上触发。
onbeforeactivate 对象要被设置为当前元素前立即触发。
onbeforecut 当选中区从文档中删除之前在源对象触发。
onbeforedeactivate 在 activeElement 从当前对象变为父文档其它对象之前立即
正则表达式验证日期格式
dashuaifu
正则表达式IT其它java其它
正则表达式验证日期格式
function isDate(d){
var v = d.match(/^(\d{4})-(\d{1,2})-(\d{1,2})$/i);
if(!v) {
this.focus();
return false;
}
}
<input value="2000-8-8" onblu
Yii CModel.rules() 方法 、validate预定义完整列表、以及说说验证
dcj3sjt126com
yii
public array rules () {return} array 要调用 validate() 时应用的有效性规则。 返回属性的有效性规则。声明验证规则,应重写此方法。 每个规则是数组具有以下结构:array('attribute list', 'validator name', 'on'=>'scenario name', ...validation
UITextAttributeTextColor = deprecated in iOS 7.0
dcj3sjt126com
ios
In this lesson we used the key "UITextAttributeTextColor" to change the color of the UINavigationBar appearance to white. This prompts a warning "first deprecated in iOS 7.0."
Ins
判断一个数是质数的几种方法
EmmaZhao
Mathpython
质数也叫素数,是只能被1和它本身整除的正整数,最小的质数是2,目前发现的最大的质数是p=2^57885161-1【注1】。
判断一个数是质数的最简单的方法如下:
def isPrime1(n):
for i in range(2, n):
if n % i == 0:
return False
return True
但是在上面的方法中有一些冗余的计算,所以
SpringSecurity工作原理小解读
坏我一锅粥
SpringSecurity
SecurityContextPersistenceFilter
ConcurrentSessionFilter
WebAsyncManagerIntegrationFilter
HeaderWriterFilter
CsrfFilter
LogoutFilter
Use
JS实现自适应宽度的Tag切换
ini
JavaScripthtmlWebcsshtml5
效果体验:http://hovertree.com/texiao/js/3.htm
该效果使用纯JavaScript代码,实现TAB页切换效果,TAB标签根据内容自适应宽度,点击TAB标签切换内容页。
HTML文件代码:
<!DOCTYPE html>
<html xmlns="http://www.w3.org/1999/xhtml"
Hbase Rest API : 数据查询
kane_xie
RESThbase
hbase(hadoop)是用java编写的,有些语言(例如python)能够对它提供良好的支持,但也有很多语言使用起来并不是那么方便,比如c#只能通过thrift访问。Rest就能很好的解决这个问题。Hbase的org.apache.hadoop.hbase.rest包提供了rest接口,它内嵌了jetty作为servlet容器。
启动命令:./bin/hbase rest s
JQuery实现鼠标拖动元素移动位置(源码+注释)
明子健
jqueryjs源码拖动鼠标
欢迎讨论指正!
print.html代码:
<!DOCTYPE html>
<html>
<head>
<meta http-equiv=Content-Type content="text/html;charset=utf-8">
<title>发票打印</title>
&l
Postgresql 连表更新字段语法 update
qifeifei
PostgreSQL
下面这段sql本来目的是想更新条件下的数据,可是这段sql却更新了整个表的数据。sql如下:
UPDATE tops_visa.visa_order
SET op_audit_abort_pass_date = now()
FROM
tops_visa.visa_order as t1
INNER JOIN tops_visa.visa_visitor as t2
ON t1.
将redis,memcache结合使用的方案?
tcrct
rediscache
公司架构上使用了阿里云的服务,由于阿里的kvstore收费相当高,打算自建,自建后就需要自己维护,所以就有了一个想法,针对kvstore(redis)及ocs(memcache)的特点,想自己开发一个cache层,将需要用到list,set,map等redis方法的继续使用redis来完成,将整条记录放在memcache下,即findbyid,save等时就memcache,其它就对应使用redi
开发中遇到的诡异的bug
wudixiaotie
bug
今天我们服务器组遇到个问题:
我们的服务是从Kafka里面取出数据,然后把offset存储到ssdb中,每个topic和partition都对应ssdb中不同的key,服务启动之后,每次kafka数据更新我们这边收到消息,然后存储之后就发现ssdb的值偶尔是-2,这就奇怪了,最开始我们是在代码中打印存储的日志,发现没什么问题,后来去查看ssdb的日志,才发现里面每次set的时候都会对同一个key