斯坦福机器学习实现与分析之五（高斯判别分析）

高斯判别分析（GDA）简介

---

　　首先，高斯判别分析的作用也是用于分类。对于两类样本，其服从伯努利分布，而对每个类中的样本，假定都服从高斯分布，则有:

\( y\;\sim\;Bernouli(\phi) \)

\( x|y=0\;\sim\;N(\mu_0, \Sigma) \)

\( x|y=1\;\sim\;N(\mu_1, \Sigma) \)

　　这样，根据训练样本，估计出先验概率以及高斯分布的均值和协方差矩阵（注意这里两类内部高斯分布的协方差矩阵相同），即可通过如下贝叶斯公式求出一个新样本分别属于两类的概率，进而可实现对该样本的分类。

　\(\begin{aligned} p(y|x)=\frac{p(x|y)p(y)}{p(x)} \end{aligned}\)

\( \begin{aligned} y=\underset{y}{argmax}\;{p(y|x)} =  \underset{y}{argmax}{ \;{\frac{p(x|y)p(y)}{p(x)}}}= \underset{y}{argmax}{\;p(x|y)p(y)} \end{aligned}\) 

 

GDA详细推导

---

　　那么高斯判别分析的核心工作就是估计上述未知量\( \phi, \mu_0, \mu_1, \Sigma \)。如何来估计这些参数？又该最大似然估计上场了。其对数似然函数为：

\( \begin{aligned} l(\phi,\mu_0,\mu_1,\Sigma) &=log{\prod_{i=1}^m{p(x^{(i)},y^{(i)})}}=log{\prod_{i=1}^m{p(x^{(i)}|y^{(i)})p(y^{(i)})}} \\  &=\sum_{i=1}^m{log\;p(x^{(i)}|y^{(i)})}+\sum_{i=1}^m{log\;p(y^{(i)})} \\ &=\sum_{i=1}^m{log\;(\;p(x^{(i)}|y^{(i)}=0)^{1-y^{(i)}}+p(x^{(i)}|y^{(i)}=1)^{y^{(i)}}\;)}+\sum_{i=1}^m{log\;p(y^{(i)})} \\ &=\sum_{i=1}^m{(1-y^{(i)})log\;p(x^{(i)}|y^{(i)}=0)}+\sum_{i=1}^m{{y^{(i)}}log\;p(x^{(i)}|y^{(i)}=1)}+\sum_{i=1}^m{log\;p(y^{(i)})} \end{aligned}\)

　　注意此函数第一部分只和\(\mu_0,\Sigma\)有关，第二部分只和\(\mu_1,\Sigma\)有关，最后一部分只和\(\phi\)有关。最大化该函数，首先求\(\phi\),先对其求偏导数：

\(\begin{aligned} \frac{\partial\;l(\phi,\mu_0,\mu_1,\Sigma)}{\partial\phi}&=\frac{\sum_{i=1}^m{log\;p(y^{(i)})}}{\partial\phi} \\&= \frac{\partial\sum_{i=1}^m{log\;\phi^{y^{(i)}}(1-\phi)^{1-y^{(i)}})}}{\partial\phi} \\&=\frac{\partial\sum_{i=1}^m{y^{(i)}\;log\;\phi+(1-y^{(i)})log(1-\phi)}}{\partial\phi} \\&=\sum_{i=1}^m{(y^{(i)}\frac{1}{\phi}-(1-y^{(i)})\frac{1}{1-\phi})} \\&=\sum_{i=1}^m{(I(y^{(i)}=1)\frac{1}{\phi}-I(y^{(i)}=0)\frac{1}{1-\phi})} \end{aligned} \)

　　此处\(I\)为指示函数。令其为0，可求解出：

\(\begin{aligned} \phi=\frac{I(y^{(i)}=1)}{I(y^{(i)}=0)+I(y^{(i)}=1)}=\frac{I(y^{(i)}=1)}{m}\end{aligned}\) 

　　同样地，对\(\mu_0\)求偏导数：

\(\begin{aligned} \frac{\partial\;l(\phi,\mu_0,\mu_1,\Sigma)}{\partial\mu_0}&=\frac{\partial\sum_{i=1}^m{(1-y^{(i)})log\;p(x^{(i)}|y^{(i)}=0)}}{\partial\mu_0} \\&=\frac{\partial\sum_{i=1}^m{(1-y^{(i)})(log\frac{1}{\sqrt{(2\pi)^n|\Sigma|}}-\frac{1}{2}(x^{(i)}-\mu_0)^T\Sigma^{-1}(x^{(i)}-\mu_0))}}{\partial\mu_0} \\&=\sum_{i=1}^m{(1-y^{(i)})(-\Sigma^{-1}(x^{(i)}-\mu_0))} \\&=\sum_{i=1}^m{-I(y^{(i)}=0)\Sigma^{-1}(x^{(i)}-\mu_0)}
\end{aligned}\) 

　　令其为0，可求解得：

\(\begin{aligned} \mu_0=\frac{\sum_{i=1}^m{I(y^{(i)}=0)x^{(i)}}}{I(y^{(i)}=0)} \end{aligned}\) 

　　根据对称性可直接得出：

\(\begin{aligned} \mu_1=\frac{\sum_{i=1}^m{I(y^{(i)}=1)x^{(i)}}}{I(y^{(i)}=1)} \end{aligned}\) 

　　下面对\( \Sigma \)求偏导数，由于似然函数只有前面两部分与\( \Sigma \)有关，则将前两部分改写如下：

\( \begin{aligned} &\sum_{i=1}^m{(1-y^{(i)})log\;p(x^{(i)}|y^{(i)}=0)}+\sum_{i=1}^m{{y^{(i)}}log\;p(x^{(i)}|y^{(i)}=1)}\\&=\sum_{i=1}^m{(1-y^{(i)})(log\frac{1}{\sqrt{(2\pi)^n|\Sigma|}}-\frac{1}{2}(x^{(i)}-\mu_0)^T\Sigma^{-1}(x^{(i)}-\mu_0))}+\sum_{i=1}^m{{y^{(i)}}(log\frac{1}{\sqrt{(2\pi)^n|\Sigma|}}-\frac{1}{2}(x^{(i)}-\mu_1)^T\Sigma^{-1}(x^{(i)}-\mu_1))}\\&=\sum_{i=1}^m{log\frac{1}{\sqrt{(2\pi)^n|\Sigma|}}}-\frac{1}{2}\sum_{i=1}^m{(x^{(i)}-\mu_{y^{(i)}})^T\Sigma^{-1}(x^{(i)}-\mu_{y^{(i)}})}\\&=\sum_{i=1}^m{(-\frac{n}{2}log(2\pi)-\frac{1}{2}log(|\Sigma|))}-\frac{1}{2}\sum_{i=1}^m{(x^{(i)}-\mu_{y^{(i)}})^T\Sigma^{-1}(x^{(i)}-\mu_{y^{(i)}})}   \end{aligned}\)

　　进而有：

\( \begin{aligned} \frac{\partial\;l(\phi,\mu_0,\mu_1,\Sigma))}{\partial\Sigma}&=-\frac{1}{2}\sum_{i=1}^m(\frac{1}{|\Sigma|}|\Sigma|\Sigma^{-1})-\frac{1}{2}\sum_{i=1}^m(x^{(i)}-\mu_{y^{(i)}})^T(x^{(i)}-\mu_{y^{(i)}})\frac{\partial\Sigma^{-1}}{\partial\Sigma}\\&=-\frac{m}{2}\Sigma^{-1}-\frac{1}{2}\sum_{i=1}^m(x^{(i)}-\mu_{y^{(i)}})^T(x^{(i)}-\mu_{y^{(i)}})(-\Sigma^{-2}))   \end{aligned}\)

　　这里推导用到了：

\( \begin{aligned} \frac{\partial|\Sigma|}{\partial\Sigma}=|\Sigma|\Sigma^{-1}\end{aligned}\)

\( \begin{aligned} \frac{\partial\Sigma^{-1}}{\partial\Sigma}=-\Sigma^{-2}\end{aligned}\) 

　　令其为0，从而求得：

\( \begin{aligned} \Sigma=\frac{1}{m}\sum_{i=1}^m(x^{(i)}-\mu_{y^{(i)}})^T(x^{(i)}-\mu_{y^{(i)}})\end{aligned}\) 

　　上面的推导似乎很复杂，但其结果却是非常简洁。通过上述公式，所有的参数都已经估计出来，需要判断一个新样本x时，可分别使用贝叶斯求出p(y=0|x)和p(y=1|x)，取概率更大的那个类。

　　实际计算时，我们只需要比大小，那么贝叶斯公式中分母项可以不计算，由于2个高斯函数协方差矩阵相同，则高斯分布前面那相同部分也可以忽略。实际上，GDA算法也是一个线性分类器，根据上面推导可以知道，GDA的分界线(面)的方程为：

        \( \begin{aligned} (1-\phi)exp((x-\mu_0)^T\Sigma^{-1}(x-\mu_0)={\phi}exp((x-\mu_1)^T\Sigma^{-1}(x-\mu_1)\end{aligned}\)

　　取对数展开后化解，可得：

 \( \begin{aligned} 2x^T\Sigma^{-1}(\mu_1-\mu_0)=\mu_1^T\Sigma^{-1}\mu_1-\mu_0^T\Sigma^{-1}\mu_0+log\;\phi-log(1-\phi)\end{aligned}\)

　　若\( \begin{aligned} A=2\Sigma^{-1}(\mu_1-\mu_0)=(a_1,a_2,...,a_n)\quad b=\mu_1^T\Sigma^{-1}\mu_1-\mu_0^T\Sigma^{-1}\mu_0+log\;\phi-log(1-\phi)\end{aligned}\)，则

 \( \begin{aligned} a_1x_1+a_2x_2+...+a_nx_n=b\end{aligned}\)

　　这就是GDA算法的线性分界面。

 

GDA实现

---

　　这里也采用前面讲逻辑回归生成的数据来进行实验，直接load进来进行处理，详见逻辑回归。GDA训练代码如下： 

 1 %mu=[mu0 mu1]

 2 function [mu sigma phi]=GDA_train(Sample)

 3     [m, n] = size(Sample); %m个样本，每个n维

 4     Y = Sample(:, end);

 5     X = [Sample(:,1:end-1)];

 6     

 7     idx = find(Y==0);

 8     mu(:,1)=mean(X(idx,:));

 9     

10     idx2 = find(Y==1);    

11     mu(:,2)=mean(X(idx2,:));

12     

13     phi = size(idx2,1)/m;

14     

15     sigma = zeros(n-1);

16     for i = 1:m

17         x = X(i, :)';

18         muc = mu(:, Y(i) + 1);

19         sigma = sigma + (x - muc) * (x - muc)';

20     end

21     sigma = sigma / m;    

22 end

View Code

 　　测试代码： 

 1 function GDA_test

 2     clear

 3     close all

 4     clc

 5     load('log_data.mat');

 6     [mu sigma phi]=GDA_train(Sample);

 7     

 8     %显示结果，以下代码不通用，样本维数增加时显示不可用

 9     figure,

10     idx = find(Sample(:,3)==1);

11     plot(Sample(idx,1), Sample(idx,2), 'g*');hold on

12     idx = find(Sample(:,3)==0);

13     plot(Sample(idx,1), Sample(idx,2), 'ro');hold on

14     

15     [t1 t2]=meshgrid(min(Sample(:,1)):.1:max(Sample(:,1)), min(Sample(:,2)):.1:max(Sample(:,2)));

16     G1=Gaussian(mu(:,1),sigma,t1,t2,1-phi);

17     G2=Gaussian(mu(:,2),sigma,t1,t2,phi);

18     contour(t1,t2,G1);hold on

19     contour(t1,t2,G2);hold on

20     

21     A=2*inv(sigma)*(mu(:,2)-mu(:,1));

22     b=mu(:,2)'*inv(sigma)*mu(:,2) - mu(:,1)'*inv(sigma)*mu(:,1) + log(phi) - log(1-phi);

23     x1=min(Sample(:,1)):.1:max(Sample(:,1));

24     x2=(b-A(1)*x1)/A(2);

25     plot(x1,x2,'m')

26 end

27 

28 function G = Gaussian(mu,sigma,t1,t2,phi)

29     for i=1:size(t1,1)

30         for j=1:size(t1,2)

31             x=[t1(i,j);t2(i,j)];

32             z=(x-mu)'*inv(sigma)*(x-mu);

33             G(i,j)=phi*exp(-z)/0.001;

34         end

35     end    

36 end

View Code

　　训练结果如下，训练样本中，正负样本均为100个，故\(\phi=0.5\)：

 

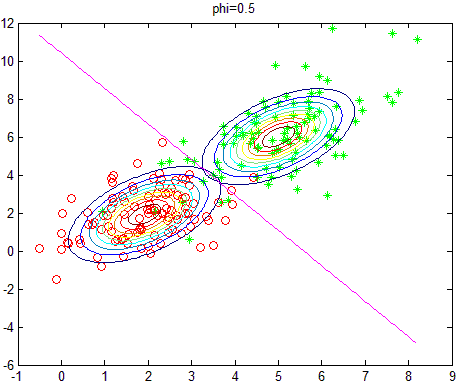
　　改变正负样本数量，即相当于改变先验概率，则实验结果如下(相应的\(\phi\)的值显示在图像标题)：

       

 

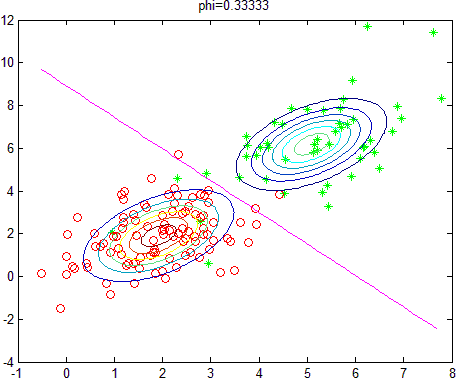
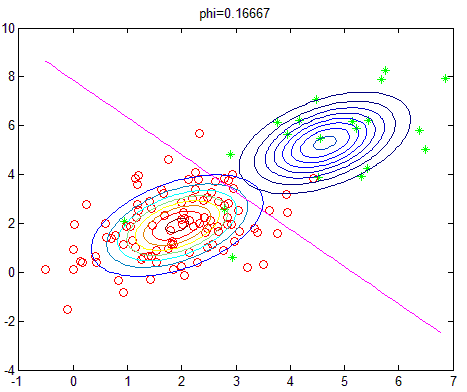
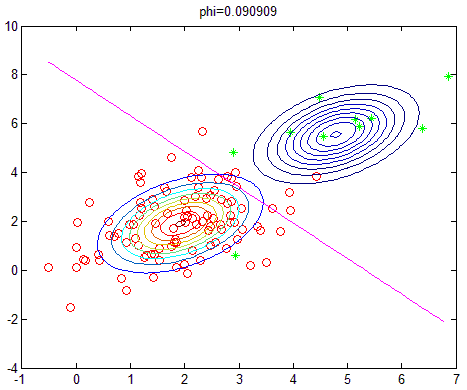
算法分析

---

　　1.与逻辑回归的关系

　　　　根据上面的结果以及贝叶斯公式，可有

 \( \begin{aligned} p(y=1|x)&=\frac{p(x|y=1)p(y=1)}{p(x)} \\&=\frac{N(\mu_1,\Sigma)\phi}{N(\mu_0,\Sigma)(1-\phi)+N(\mu_1,\Sigma)\phi}\\&=1/{(1+\frac{N(\mu_0,\Sigma))}{N(\mu_1,\Sigma)}\frac{1-\phi}{\phi})} \end{aligned}\)

　　　　而

\( \begin{aligned} \frac{N(\mu_0,\Sigma)}{N(\mu_1,\Sigma)}&= exp\{(x-\mu_0)^T\Sigma^{-1}(x-\mu_0)-(x-\mu_1)^T\Sigma^{-1}(x-\mu_1)\}\\&=exp\{ 2(\mu_1-\mu_0)^T\Sigma^{-1}x+(\mu_0^T\Sigma\mu_0-\mu_1^T\Sigma\mu_1)\}\end{aligned}\)

　　　　那么,令

\( \begin{aligned}
2\Sigma^{-1}(\mu_1-\mu_0) =(\theta_1,\theta_2,...,\theta_n)^T\\
\theta_0=\mu_0^T\Sigma\mu_0-\mu_1^T\Sigma\mu_1+log\frac{1-\phi}{\phi}\\
\end{aligned}\)

　　　　则

\( \begin{aligned}
p(y=1|x)=\frac{1}{1+exp(\theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n)}
\end{aligned}\)

　　　　这不就是逻辑回归的形式么？

　　　　在推导逻辑回归的时候，我们并没有假设类内样本是服从高斯分布的，因而GDA只是逻辑回归的一个特例，其建立在更强的假设条。故两者效果比较：

　　　　a.逻辑回归是基于弱假设推导的，则其效果更稳定，适用范围更广

　　　　b.数据服从高斯分布时，GDA效果更好

　　　　c.当训练样本数很大时，根据中心极限定理，数据将无限逼近于高斯分布，则此时GDA的表现效果会非常好

 

　　2.为何要假设两类内部高斯分布的协方差矩阵相同？

　　　　从直观上讲，假设两个类的高斯分布协方差矩阵不同，会更加合理（在混合高斯模型中就是如此假设的），而且可推导出类似上面简洁的结果。

　　　　假定两个类有相同协方差矩阵，分析具有以下几点影响：

　　　　A．当样本不充分时，使用不同协方差矩阵会导致算法稳定性不够；过少的样本甚至导致协方差矩阵不可逆，那么GDA算法就没法进行

　　　　B．使用不同协方差矩阵，最终GDA的分界面不是线性的，同样也推导不出GDA的逻辑回归形式

 

　　3.使用GDA时对训练样本有何要求？

　　　　首先，正负样本数的比例需要符合其先验概率。若是预先明确知道两类的先验概率，那么可使用此概率来代替GDA计算的先验概率；若是完全不知道，则可以公平地认为先验概率为　　50%。

　　　　其次，样本数必须不小于样本特征维数，否则会导致协方差矩阵不可逆，按照前面分析应该是多多益善。