图形学理论 光照模型
光照模型
1. Lambert模型
理想漫反射模型，各个方向一样。
2.Phong（1975）[1]
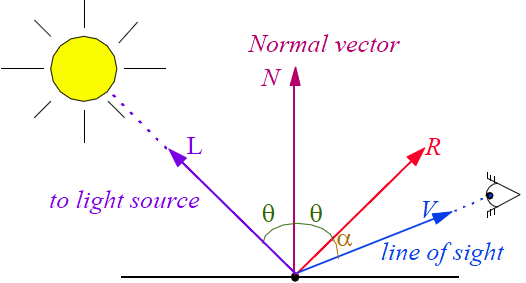
经验模型，R和V的夹角决定镜面高光的强度。
3.Blinn-Phong（1977）[2]
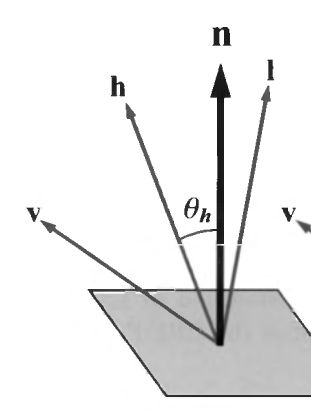
引入了半角向量的概念，对Phong模型进行了改进，镜面高光由n和h的夹角决定。
4. Cook-Torrance 模型（1982）[3]
用模型模拟了金属和塑料材质，考虑到了入射角变化时发生的颜色偏移。
基本反射模型：
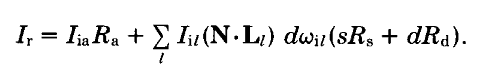
其中环境光和漫反射分量不依赖于观察者的位置。
假设表面是由微面元组成的，镜面分量写为：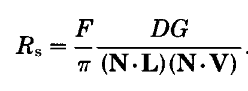
加入了：几何项G、Fresnel项、粗糙度项D.
粗糙度项D：代表了可以有效反射光的那一部分微面元所占的比例。
有多种分布函数：
高斯分布模型：
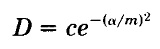
Beckmann分布函数：
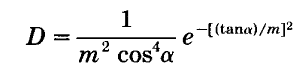
几何项G：几何衰减项，表现了微小面元之间的互相遮挡（shadowing and masking）所造成的影响。
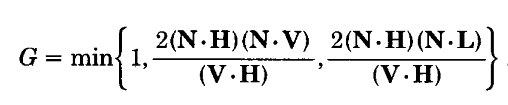
Fresnel项F:描述了在每一个微面元上光是如何反射。与入射角和波长相关。
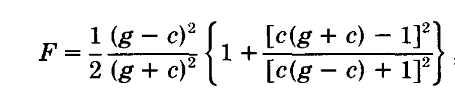
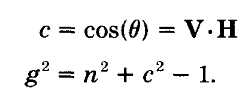
通过垂直入射时的公式，可以解出折射率n，然后再将得到的n代入原来的公式即可得到其他各个角度下的F。
这个过程可以对不同的波长重复多次，以获得反射的方向和光谱分布。
几点理论：当入射角接近90°的时候，F接近于1，反射光的颜色接近于光源的颜色。颜色偏移在入射角接近90°变得很重要。可以用查找表简化计算。
镜面反射的颜色通常是材料的颜色而不是光源的颜色。
塑料使用白色的镜面高光，漫反射成分大而镜面反射成分小。这种物体的漫反射颜色和镜面反射颜色通常不同。
金属的反射一般发生在表面，漫反射分量很小，有时甚至可以忽略。粗糙度的值m也很小。
5．Kajiya各向异性反射模型（1985） [4]
根据电磁波理论推导出来的模型，反映了各向异性表面的反射和折射。
6.Oren-Nayar 模型（1994）[5]
提出对于体反射来说，lambertian的模型不能正确体现其效果。
本模型主要对粗糙表面的物体建模，比如石膏、沙土、陶瓷还有布。
用了一系列的lambert微面元，考虑了微小面元之间的相互遮挡（shadowing and masking）和互相反射照明。
7.Minnaert 漫反射模型（Marcel Minnaert 1941）
丝绒 反射公式
8.Ward 反射模型
各向同性。
各项异性。
9.Schlick反射模型
简化了Phong模型的指数运算。
10. Xiao D. He模型（1991）[6]
一个非常复杂的综合物理模型。
但仍然是一个反射模型。
基于物理光学，描述了表面的镜面反射、有方向的漫反射、均匀漫反射。
反射光依赖于波长、入射角、两个表面粗糙度系数、表面折射率。
可以应用到金属、非金属、塑料（光滑、粗糙）。
1. Phong, B.T., Illumination for computer generated pictures 1975.
2. Blinn, J.F., Models of light reflection for computer synthesized pictures 1977.
3. Cook, R.L. and K.E. Torrance, A Reflectance Model for Computer Graphics 1982.
4. Kajiya, J.T., Anisotropic reflection models 1985: p. 15 - 21
5. Oren, P. and P.K. Nayar, Generalization of Lambert’s Reflectance Model. 1994: p. 239 - 246
6. He, X.D., et al., A comprehensive physical model for light reflection 1991: p. 175 - 186