决策树算法--ID3算法

决策树（Decision Tree)是一类常见的机器学习方法，是一种非常常用的分类方法，它是一种监督学习。常见的决策树算法有ID3，C4.5、C5.0和CART（classification and regression tree），CART的分类效果一般要优于其他决策树。

决策树是基于树状结构来进行决策的，一般地，一棵决策树包含一个根节点、若干个内部节点和若干个叶节点。

• 每个内部节点表示一个属性上的判断
• 每个分支代表一个判断结果的输出
• 每个叶节点代表一种分类结果。
• 根节点包含样本全集

决策树学习的目的是为了产生一棵泛化能力强，即处理未见示例能力强的决策树，其基本流程遵循简单且直管的“分而治之”（divide-and-conquer）策略。

本文主要介绍ID3算法，ID3算法的核心是根据信息增益来选择进行划分的特征，然后递归地构建决策树。

特征选择

特征选择也即选择最优划分属性，从当前数据的特征中选择一个特征作为当前节点的划分标准。 随着划分过程不断进行，希望决策树的分支节点所包含的样本尽可能属于同一类别，即节点的“纯度”越来越高。

熵（entropy）

熵表示事务不确定性的程度，也就是信息量的大小（一般说信息量大，就是指这个时候背后的不确定因素太多），熵的公式如下：
$$Entropy=-\sum _{i=1}^{n}p(x_i)\ast lo{g}_{2}p(x_i)$$
其中，$p(x_i)$是分类$x_i$出现的概率，n是分类的数目。可以看出，熵的大小只和变量的概率分布有关。

对于在X的条件下Y的条件熵，是指在X的信息之后，Y这个变量的信息量（不确定性）的大小，计算公式如下：
$$Entropy(Y|X)=\sum _{i=1}^{n}p(x_i)\ast Entropy(Y|x_i)$$
例如，当只有A类和B类的时候，$p(A)=p(B)=0.5$，熵的大小为：
$$Entropy=-(0.5\ast lo{g}_2(0.5)+0.5\ast lo{g}_2(0.5))=1$$
当只有A类或只有B类时，
$$Entropy=-(1\ast lo{g}_2(1))=0$$
所以当Entropy最大为1的时候，是分类效果最差的状态，当它最小为0的时候，是完全分类的状态。因为熵等于零是理想状态，一般实际情况下，熵介于0和1之间 。

熵的不断最小化，实际上就是提高分类正确率的过程。

信息增益（information gain）

信息增益：在划分数据集之前之后信息发生的变化，计算每个特征值划分数据集获得的信息增益，获得信息增益最高的特征就是最好的选择。

定义属性A对数据集D的信息增益为infoGain(D|A)，它等于D本身的熵，减去 给定A的条件下D的条件熵，即：
$$infoGain(D|A)=Entropy(D)-Entropy(D|A)$$
其中$A=[a_1,a_2,...,a_k]$，K个值。

信息增益的意义：引入属性A后，原来数据集D的不确定性减少了多少。

计算每个属性引入后的信息增益，选择给D带来的信息增益最大的属性，即为最优划分属性。一般，信息增益越大，则意味着使用属性A来进行划分所得到的的“纯度提升”越大。

步骤

1. 从根节点开始，计算所有可能的特征的信息增益，选择信息增益最大的特征作为节点的划分特征；
2. 由该特征的不同取值建立子节点；
3. 再对子节点递归1-2步，构建决策树；
4. 直到没有特征可以选择或类别完全相同为止，得到最终的决策树。

Python实现

使用ID3算法来预测隐形眼镜类型，判断患者需要佩戴的镜片类型。

数据集来源点这里下载，下载下图这两个文件

需要注意的是，lenses.data文件中的数据都是数值型，为了画出决策树，所以我这里根据lenses.name文件中的内容，将lenses.data文件中的数值都转换为对应的字符串了。转换后的数据如下

具体代码如下

from math import log
import operator
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['font.sans-serif'] = [u'SimHei']
matplotlib.rcParams['axes.unicode_minus'] = False

def calcShannonEnt(dataSet):
    """
    计算给定数据集的香农熵
    :param dataSet:给定的数据集
    :return:返回香农熵
    """
    numEntries = len(dataSet)
    labelCounts ={}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] =0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for label in labelCounts.keys():
        prob = float(labelCounts[label])/numEntries
        shannonEnt -= prob*log(prob,2)
    return shannonEnt

def splitDataSet(dataSet,axis,value):
    """按照给定特征划分数据集"""
    retDataSet = []  # 创建新的list对象，作为返回的数据
    for featVec in dataSet:
        if featVec[axis]==value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])  # 抽取
            retDataSet.append(reducedFeatVec)
    return retDataSet

def chooseBestFeatureToSplit(dataSet):
    """选择最好的数据集划分方式"""
    numFeatures = len(dataSet[0])-1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0
    bestFeature = -1
    for i in range(numFeatures):
        # 获取第i个特征值，不重复的值
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        # 计算每种划分方式的信息熵newEntropy
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet,i,value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob*calcShannonEnt(subDataSet)
        # 信息增益是熵的减少或数据无序度的减少
        # 比较所有特征中的信息增益，返回最好特征划分的索引值
        infoGain = baseEntropy-newEntropy
        if infoGain > bestInfoGain:
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

def majorityCnt(classList):
    """获取出现次数最好的分类名称"""
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
    sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
    return sortedClassCount[0][0]

def createTree(dataSet,labels):
    """创建树"""
    classList = [example[-1] for example in dataSet]
    # 如果类别完全相同，则停止继续划分
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    # 遍历完所有特征时返回出现次数最多的类别
    if len(dataSet) ==1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del labels[bestFeat]
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
    return myTree

# 使用文本注解绘制树节点
def plotNode(nodeTxt,centerPt,parentPt,nodeType):
    """绘制带箭头的节点"""
    createPlot.ax1.annotate(nodeTxt,xy=parentPt,xycoords='axes fraction',xytext= centerPt,textcoords='axes fraction',va='center',ha='center',bbox=nodeType,arrowprops=arrow_args)

def createPlot():
    """绘制树节点"""
    fig = plt.figure(1,facecolor='white')
    fig.clf()
    createPlot.ax1 = plt.subplot(111,frameon=False)
    plotNode('决策节点',(0.5,0.1),(0.1,0.5),decisionNode)
    plotNode('叶节点',(0.8,0.1),(0.3,0.8),leafNode)
    plt.show()

def getNumLeafs(myTree):
    """获取叶节点的数目"""
    numLeafs = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':
            numLeafs += getNumLeafs(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs

def getTreeDepth(myTree):
    """获取树的层数"""
    maxDepth = 0
    firstStr =list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ =='dict':
            thisDepth = 1+getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth:
            maxDepth = thisDepth
    return maxDepth

def plotMidText(cntPt,parentPt,txtString):
    """在父子节点间填充文本信息"""
    xMid = (parentPt[0]-cntPt[0])/2+cntPt[0]
    yMid = (parentPt[1]-cntPt[1])/2+cntPt[1]
    createPlot.ax1.text(xMid,yMid,txtString)

def plotTree(myTree,parentPt,nodeTxt):
    """绘制树形图"""
    numLeafs = getNumLeafs(myTree)
    depth = getTreeDepth(myTree)
    firstStr = list(myTree.keys())[0]
    cntrPt = (plotTree.xOff + (1 + float(numLeafs))/2/plotTree.totalW,plotTree.yOff)
    plotMidText(cntrPt,parentPt,nodeTxt)
    plotNode(firstStr,cntrPt,parentPt,decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff-1/plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':
            plotTree(secondDict[key],cntrPt,str(key))
        else:
            plotTree.xOff = plotTree.xOff + 1/plotTree.totalW
            plotNode(secondDict[key],(plotTree.xOff,plotTree.yOff),cntrPt,leafNode)
            plotMidText((plotTree.xOff,plotTree.yOff),cntrPt,str(key))
    plotTree.yOff = plotTree.yOff + 1 / plotTree.totalD

def createPlot(inTree):
    """创建绘图区"""
    fig = plt.figure(1,facecolor='white')
    fig.clf()
    axprops = dict(xticks=[],yticks=[])
    createPlot.ax1 = plt.subplot(111,frameon=False,**axprops)
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5/plotTree.totalW
    plotTree.yOff = 1.0
    plotTree(inTree,(0.5,1.0),'')
    plt.show()

def classify(inputTree,featLabels,testVec):
    """使用决策树的分类函数"""
    firstStr = list(inputTree.keys())[0]
    secondDict = inputTree[firstStr]
    featIndex = featLabels.index(firstStr)
    for key in secondDict.keys():
        if testVec[featIndex]==key:
            if type(secondDict[key]).__name__ == 'dict':
                classLabel = classify(secondDict[key],featLabels,testVec)
            else:
                classLabel = secondDict[key]
    return classLabel
def lenses_test():
    """使用决策树预测隐形眼镜类型"""
    fr = open('lenses.txt')
    lenses = [inst.strip().split('  ') for inst in fr.readlines()]
    lensesLabel = ['age','prescript','astigmatic','tearRate']
    lensesTree = createTree(lenses,lensesLabel)  # 创建树
    print(lensesTree)
    createPlot(lensesTree)  # 绘制树
   
if __name__ == '__main__':
    decisionNode = dict(boxstyle='sawtooth',fc='0.8')
    leafNode = dict(boxstyle='round4',fc='0.8')
    arrow_args = dict(arrowstyle='<-')
    lenses_test()

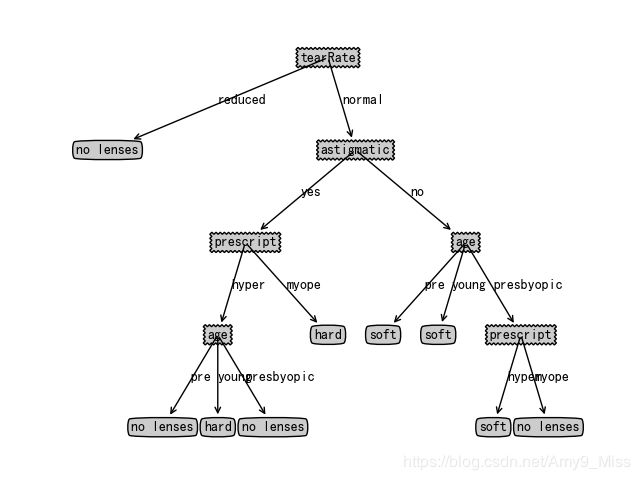
运行结果如下

总结

ID3算法适用离散型数据，主要是根据信息增益来选择进行划分的特征，然后递归地构建决策树。它的主要优缺点如下：

优点：

• 计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据

缺点：

• 没有剪枝，可能会产生过度匹配问题，需要进行剪枝
• 采用信息增益作为选择最优划分特征的标准，然而信息增益会偏向那些取值较多的特征

相关链接

书籍：《机器学习实战》、周志华的西瓜书《机器学习》

隐形眼镜数据集