图像处理常见滤波器--均值滤波、方框滤波、高斯滤波(上)
图像处理常见滤波器–均值滤波、方框滤波、高斯滤波(上)
滤波,是用来将信号中特定波段频率踢出的操作,而用在图像的处理之中,则便是将图像之中的像素点进行一系列的基本运算的结果,用来提取,或者说是展现隐藏在图像之中的数学信息的手段。
什么是线性滤波?
一个二维的滤波器矩阵(或者叫卷积核),一个需要处理的二维图像,对于二维图像的每一个像素点,计算它的邻域像素和滤波器矩阵的对应元素的乘积,然后加起来,作为该像素位置的值,就这样,完成了一次滤波过程。
滤波器的数学表达形式:
在 M × N M \times N M×N 的图像 f f f 上,使用 m × n m \times n m×n 的滤波器
g ( x , y ) = ∑ s = − a a ∑ t = − b b w ( s , t ) f ( x + s , y + t ) {\rm{g}}(x,y) = \sum\limits_{s = - a}^a {\sum\limits_{t = - b}^b {w(s,t)f(x + s,y + t)} } g(x,y)=s=−a∑at=−b∑bw(s,t)f(x+s,y+t)
其中, m = 2 a + 1 m=2a+1 m=2a+1, n = 2 b + 1 n=2b+1 n=2b+1, w ( s , t ) w(s,t) w(s,t) 是滤波器系数, f ( x , y ) f(x,y) f(x,y) 是图像值;
空间滤波器也可以写成简化的形式:
R = w 1 z 1 + w 1 z 1 + . . . + w m n z m n = ∑ i = 1 m n w i z i R = w_1z_1 + w_1z_1 + ... + w_{mn}z_{mn} = \sum\limits_{i = 1}^{mn} w_iz_i R=w1z1+w1z1+...+wmnzmn=i=1∑mnwizi
其中, w w w 是滤波器系统, z z z 是与该系数对应图像灰度值, m n mn mn 为滤波器中包含的像素点总数
均值滤波
均值滤波是典型的线性滤波算法,它是指在图像上对目标像素给一个模板,该模板包括了其周围的临近像素(以目标象素为中心的周围8个像素,构成一个滤波模板,即去掉目标像素本身),再用模板中的全体像素的平均值来代替原来像素值。均值滤波其实就是对目标像素及周边像素取平均值后再填会目标像素来实现滤波目的的方法。
不足之处:均值滤波本身存在着固有的缺陷,即它不能很好地保护图像细节,在图像去噪的同时也破坏了图像的细节部分,从而使图像变得模糊,不能很好地去除噪声点。
均值滤波的权重系数模板:
K = 1 K w × K h [ 1 1 ⋯ 1 1 1 ⋯ 1 ⋮ ⋮ ⋮ ⋮ 1 1 ⋯ 1 ] K = \frac{1}{{{K_w} \times {K_h}}}\left[ {\begin{array}{ccc} 1&1& \cdots &1\\ 1&1& \cdots &1\\ \vdots & \vdots & \vdots & \vdots \\ 1&1& \cdots &1 \end{array}} \right] K=Kw×Kh1⎣⎢⎢⎢⎡11⋮111⋮1⋯⋯⋮⋯11⋮1⎦⎥⎥⎥⎤
因为模板的权值都是1,所以整个图像的滤波也可以表示成下面式子的样子:
g ( x , y ) = 1 M ∑ f ( x , y ) ( x , y ) ∈ N g(x,y) = \frac{1}{M}\sum {{\rm{f}}(x,y)\begin{array}{ccc} {}&{(x,y) \in N} \end{array}} g(x,y)=M1∑f(x,y)(x,y)∈N
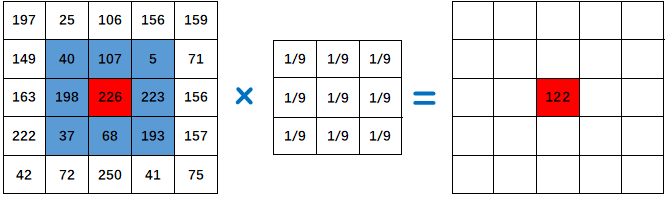
式子中 g ( x , y ) g(x,y) g(x,y)为均值滤波后的图像, f ( x , y ) f(x,y) f(x,y)为原始图像, M M M为模板中包括当前像素在内的像素个数, N N N 为模板领域像素点集合。下图也更好的解释了滤波的过程(其实就是卷积),即 40 + 107 + 5 + 198 + 226 + 223 + 37 + 68 + 193 9 \frac {40+107+5+198+226+223+37+68+193}{9} 940+107+5+198+226+223+37+68+193
话不多说,用代码实现以下,这个在opencv里面有相应的库函数,直接调用就可以了,但是为了更好的理解什么事平滑滤波,这里先使用自己写的代码实现以下,然后和opencv里的库函数做对比,以验证实现的是否正确。
代码
# -*- coding: utf-8 -*-
"""
Created on Wed Aug 14 11:05:54 2019
@author: shengzhanhe
@e-mail: [email protected]
"""
import cv2
import numpy as np
def mean_filter(img_path, kernel_size):
k_w, k_h = kernel_size
img = cv2.imread(img_path)
img_w, img_h, channel = img.shape
# 这里为了可以提取到边框的信息,并且保持和原图大小想到,采用边界补零的操作
res_b = np.zeros([img_w+k_w-1, img_h+k_h-1])
res_g = np.zeros([img_w+k_w-1, img_h+k_h-1])
res_r = np.zeros([img_w+k_w-1, img_h+k_h-1])
# 把图像中每一个通道分离出来,放在相应的地方
res_b[(k_w-1)//2:(1-k_w)//2, (k_h-1)//2:(1-k_h)//2] = cv2.split(img)[0]
res_g[(k_w-1)//2:(1-k_w)//2, (k_h-1)//2:(1-k_h)//2] = cv2.split(img)[1]
res_r[(k_w-1)//2:(1-k_w)//2, (k_h-1)//2:(1-k_h)//2] = cv2.split(img)[2]
# 对每一个通道滤波
b = fileter(res_b, kernel_size)
g = fileter(res_g, kernel_size)
r = fileter(res_r, kernel_size)
# 通道融合
res_img = cv2.merge([b, g, r])
return res_img
def fileter(img_mat, kernel_size):
k_w, k_h = kernel_size
# 定义均值滤波器的权值
kernel = np.ones([k_w, k_h])/(k_w*k_h)
w, h = img_mat.shape
fileter_res = np.zeros([w-k_w+1, h-k_h+1])
# 对图像中的每一个像素值进行滤波
for i in range(h-k_h):
for j in range(w-k_w):
pix = np.sum(img_mat[j:j+k_w,i:i+k_h]*kernel)
fileter_res[j,i] = int(pix)
return fileter_res.astype(np.uint8)
# opencv实现均值滤波
def opencv_blur(img_path):
img = cv2.imread(img_path)
result = cv2.blur(img, (3, 3))
return result
if __name__ == "__main__":
path = './lenaNoise.png'
image = cv2.imread(path)
# 手动实现,使用3*3的卷积核
my_img = mean_filter(path, (3,3))
# 使用opencv里的库函数
opencv_img = opencv_blur(path)
cv2.imshow("original", image)
cv2.imshow('my_img', my_img)
cv2.imshow('opencv', opencv_img)
cv2.imwrite('my_img.png', my_img)
cv2.imwrite('opencv.png', opencv_img)
cv2.waitKey(0)
3 * 3滤波器的效果
5 * 5滤波器的效果
7 * 7滤波器
可以看出自己实现的结果和opencv库函数是一样的,从滤波器的大小上也可以得出,滤波器(卷积核)越大,图像越平滑,但也显得更模糊。
方框滤波
方框滤波和均值滤波核基本上是一致的,主要的区别是要不要归一化处理,如果使用归一化处理,方框滤波就是均值滤波。
方框滤波的权重系数模板
K = 1 α [ 1 1 ⋯ 1 1 1 ⋯ 1 ⋮ ⋮ ⋮ ⋮ 1 1 ⋯ 1 ] , α = { 1 K w × K h , n o r m a l i z e = t r u e 1 , n o r m a l i z e = f a l s e K = \frac{1}{\alpha }\left[ {\begin{array}{ccc} 1&1& \cdots &1\\ 1&1& \cdots &1\\ \vdots & \vdots & \vdots & \vdots \\ 1&1& \cdots &1 \end{array}} \right],\begin{array}{ccc} {}&{\alpha = \left\{ {\begin{array}{ccc} {\frac{1}{{{K_w} \times {K_h}}},\begin{array}{ccc} {}&{normalize = true} \end{array}}\\ {1,\begin{array}{ccc} {\begin{array}{ccc} {\begin{array}{ccc} {}&{} \end{array}}&{} \end{array}}&{normalize = false} \end{array}} \end{array}} \right.} \end{array} K=α1⎣⎢⎢⎢⎡11⋮111⋮1⋯⋯⋮⋯11⋮1⎦⎥⎥⎥⎤,α={Kw×Kh1,normalize=true1,normalize=false
可以看出让方框滤波不采用归一化的时候,使用卷积核操作很容易使得像素值溢出,即对应的像素值为255。
这里就直接使用opencv里面的库函数,然后要是自己需要写代码的话,把上面的代码里添加一个 α \alpha α的判定条件就可以啦
代码如下
# -*- coding: utf-8 -*-
"""
Created on Wed Aug 14 11:05:54 2019
@author: shengzhanhe
@e-mail: [email protected]
"""
import cv2
# 方框滤波进行归一化处理就和均值滤波一样
image = cv2.imread('./lenaNoise.png')
# -1表示与原始图像深度一致
# 归一化处理
res1 = cv2.boxFilter(image, -1, (5,5), normalize=1)
# 不进行归一化处理
res2 = cv2.boxFilter(image, -1, (5,5), normalize=0)
res3 = cv2.boxFilter(image, -1, (3,3), normalize=0)
cv2.imshow('res1', res1)
cv2.imshow('res2', res2)
cv2.imshow('res3', res3)
cv2.waitKey()
cv2.destroyAllWindows()
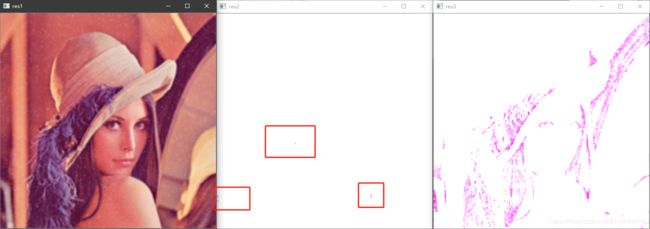
从图上可以看出来,做了归一化处理的方框滤波就是均值滤波,然后没有做归一化处理的,图上好多都变成了白色,特别是 5 × 5 5 \times 5 5×5 大小的卷积核,基本上都是白的,最右侧是 3 × 3 3 \times 3 3×3 的卷积核的效果。
高斯滤波
高斯滤波是一种线性滤波。就是对整幅图像进行加权平均的过程,每个像素点的值都由其本身和邻域内的其它像素值经过加权平均后得到。它是图像平滑的一种重要的方式,能有效地消除和抑制噪声,达到图像平滑的效果。同时,相比于平均模板而言,效果更加自然。更加自然的意思,实际上说相对于就是适当地降低平滑后的模糊程度。
一维高斯函数
g ( x ) = 1 σ 2 π e − ( x − μ ) 2 2 σ 2 {\rm{g}}(x) = \frac{1}{{\sigma \sqrt {2\pi } }}{e^{\frac{{ - {{(x - \mu )}^2}}}{{2{\sigma ^2}}}}} g(x)=σ2π1e2σ2−(x−μ)2
二维高斯函数
g ( x , y ) = 1 σ 2 π e − ( x − μ ) 2 + ( y − v ) 2 2 σ 2 {\rm{g}}(x,y) = \frac{1}{{\sigma \sqrt {2\pi } }}{e^{ - \frac{{{{(x - \mu )}^2} + {{(y - v)}^2}}}{{2{\sigma ^2}}}}} g(x,y)=σ2π1e−2σ2(x−μ)2+(y−v)2
这里把 μ = 0 , v = 0 , σ = 0.5 \mu=0, v=0, \sigma = 0.5 μ=0,v=0,σ=0.5,画出高斯函数的一维和二维图像
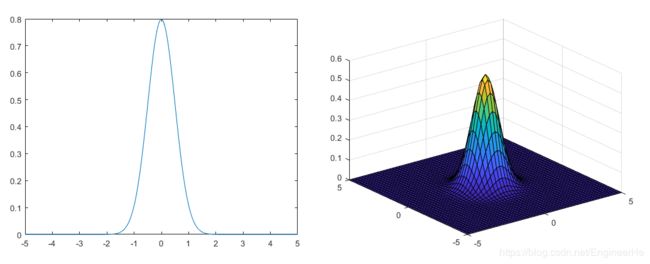
有了公式以后高斯滤波器的核要怎么计算呢?一般是以核的中心为原点建立坐标系,在图像计算中,以中心坐标为基准,所以$\mu=0, v=0 $; 以一个3*3的滤波核为例,分三步:1.画出坐标模板,2.计算每一个位置的值,3.归一化,然后以 σ = 1.5 \sigma = 1.5 σ=1.5 为例

上图操作中,归一化的目的是让权重的和等于1,如果大于1的话,滤镜会使得图像偏亮,小于1的话会使得图像偏暗。还有这样解释的12:归一化之后,通过卷积计算出来的模板中心像素被限制到了0-255的灰度区间中。假若某一邻域内所有像素的灰度值为255,利用该模板进行卷积之后,求得的模板中心像素灰度值仍然为255;假若计算出来的高斯模板参数之和小于1,那么通过该模板进行卷积之后,模板中心像素的灰度值将小于255,偏离了实际的灰度值,产生了误差。
如果对精度没有要求的话,常用的 σ = 1 \sigma=1 σ=1 的模板有下面两个
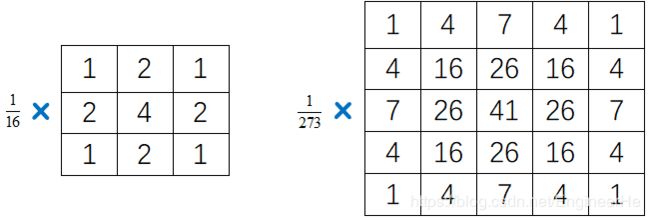
对于上述模板,你如果更加上述的公式计算的话,可能会发现有所偏差,这里我搜到的一种解释是这样的12:高斯模板实际上也就是模拟高斯函数的特征,具有对称性并且数值由中心向四周不断减小,这个模板刚好符合这样的特性,并且非常简单,容易被大家接受,于是就比较经典!
下面是具体代码的实现,包括使用自己手动实现,和opencv库函数(库函数就一句话,很简单),实现的过程中,主要是当 σ < = 0 \sigma<=0 σ<=0 的情况,这里我参考的opencv库函数的处理方法,公式如下:
σ = ( σ 2 − 1 ) × 0.3 + 0.8 \sigma {\rm{ = (}}\frac{\sigma }{2}{\rm{ - }}1) \times 0.3 + 0.8 σ=(2σ−1)×0.3+0.8
代码
# -*- coding: utf-8 -*-
"""
Created on Wed Aug 14 11:05:54 2019
@author: shengzhanhe
@e-mail: [email protected]
"""
import math
import numpy as np
import cv2
def gauss_func(x, y, sigma=0):
res = 0
# 高斯函数
res = 1.0/(2*math.pi*sigma**2)*math.exp(-(x**2+y**2)/(2*sigma**2))
return res
def create_gauss_kernel(kernel_size, sigma):
w,h = kernel_size
center_x, center_y = w//2, h//2
# sigma是否是正数,不是正数的话,需要单独处理
if sigma > 0:
sigma = sigma
else:
sigma = 0.3*((w-1)*0.5-1) + 0.8
# 计算高斯核中的每一个权值
kernel = np.zeros((w,h))
for i in range(h):
for j in range(w):
x = j - center_x
y = center_y - i
kernel[i, j] = gauss_func(x, y, sigma)
# normalize
kernel = kernel/np.sum(kernel)
return kernel
def fileter(img_mat, kernel_size, sigma):
k_w, k_h = kernel_size
# 高斯滤波器
kernel = create_gauss_kernel(kernel_size, sigma)
w, h = img_mat.shape
fileter_res = np.zeros([w-k_w+1, h-k_h+1])
# 对图像中的每一个像素值进行滤波
for i in range(h-k_h):
for j in range(w-k_w):
pix = np.sum(img_mat[j:j+k_w,i:i+k_h]*kernel)
fileter_res[j,i] = int(pix)
return fileter_res.astype(np.uint8)
def gauss_filter(img_path, kernel_size, sigma):
k_w, k_h = kernel_size
img = cv2.imread(img_path)
img_w, img_h, channel = img.shape
# 这里为了可以提取到边框的信息,并且保持和原图大小想到,采用边界补零的操作
res_b = np.zeros([img_w+k_w-1, img_h+k_h-1])
res_g = np.zeros([img_w+k_w-1, img_h+k_h-1])
res_r = np.zeros([img_w+k_w-1, img_h+k_h-1])
# 把图像中每一个通道分离出来,放在相应的地方
res_b[(k_w-1)//2:(1-k_w)//2, (k_h-1)//2:(1-k_h)//2] = cv2.split(img)[0]
res_g[(k_w-1)//2:(1-k_w)//2, (k_h-1)//2:(1-k_h)//2] = cv2.split(img)[1]
res_r[(k_w-1)//2:(1-k_w)//2, (k_h-1)//2:(1-k_h)//2] = cv2.split(img)[2]
# 对每一个通道滤波
b = fileter(res_b, kernel_size, sigma)
g = fileter(res_g, kernel_size, sigma)
r = fileter(res_r, kernel_size, sigma)
# 通道融合
res_img = cv2.merge([b, g, r])
return res_img
if __name__ == '__main__':
path = './lenaNoise.png'
image = cv2.imread(path)
# 调用opencv库函数
opencv_img = cv2.GaussianBlur(image, (3,3), 0)
# 手动实现高斯滤波
my_img = gauss_filter(path, (3,3), 0)
cv2.imshow("original", image)
cv2.imshow('my_img', my_img)
cv2.imshow('opencv_img', opencv_img)
cv2.imwrite('opencv_gauss3.png', opencv_img)
cv2.imwrite('gauss3.png', my_img)
cv2.waitKey(0)
3 * 3 滤波器
5 * 5 滤波器
7 * 7的滤波器
从图上可以看出,高斯滤波不同卷积核去燥的效果不一样,卷积核越大图像越模糊,但是相对相对于均值滤波而言,高斯滤波去燥的同时,也尽可能的保存了边缘信息(可以理解为模糊程度没有那么大,但是也达到了去噪的效果)!
欢迎大家关注我的个人公众号,同样的也是和该博客账号一样,专注分享技术问题,我们一起学习进步

https://blog.csdn.net/lz0499/article/details/54015150 ↩︎ ↩︎
https://lps-683.iteye.com/blog/2251180 ↩︎ ↩︎