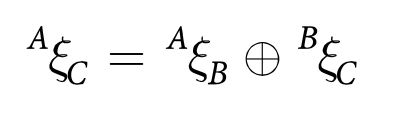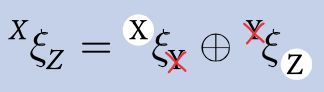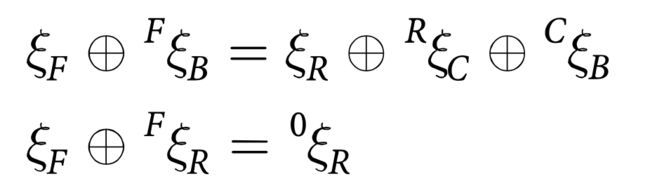Chapter 2 Representing Position and Orientation
A fundamental requirement in robotics and computer vision is to represent the position and orientation of objects in an environment. Such objects include robots, cameras, work pieces, obstacles and paths.
A point in space is a familiar concept from mathematics and can be described by a coordinate vector, also known as a bound vector, as shown in Fig. 2.1a. The vector represents the displacement of the point with respect to some reference coordinate frame. A coordinate frame, or Cartesian coordinate system, is a set of orthogonal axes which intersect at a point known as the origin.
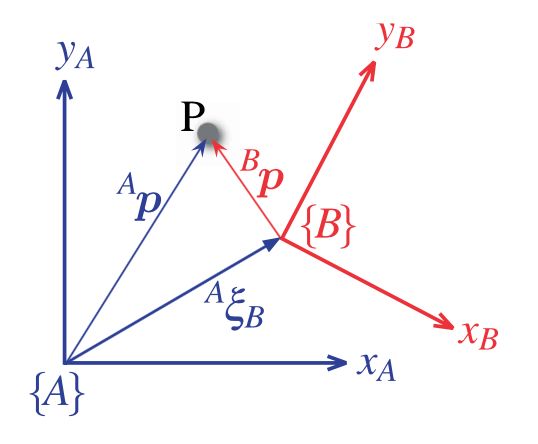
More frequently we need to consider a set of points that comprise some object. We assume that the object is rigid and that its constituent points maintain a constant relative position with respect to the object’s coordinate frame as shown in Fig. 2.1b. Instead of describing the individual points we describe the position and orientation of the object by the position and orientation of its coordinate frame. A coordinate frame is labelled, {B} in this case, and its axis labels xB and yB adopt the frame’s label as their subscript.
a The point P is described by a coordinate vector with respect to an absolute coordinate frame. b The points are described with respect to the object’s coordinate frame {B} which in turn is described by a relative pose ξB. Axes are denoted by thick lines with an open arrow, vectors by thin lines with a swept arrow head and a pose by a thick line with a solid head
The point P can be described by coordinate vectors relative to either frame {A} or {B}. The pose of {B} relative to {A} is AξB
The position and orientation of a coordinate frame is known as its pose and is shown graphically as a set of coordinate axes. The relative pose of a frame with respect to a reference coordinate frame is denoted by the symbol ξ – pronounced ksi. Figure 2.2 shows two frames {A} and {B} and the relative pose AξB which describes {B} with respect to {A}. The leading superscript denotes the reference coordinate frame and the subscript denotes the frame being described. We could also think of AξB as describing some motion – imagine picking up {A} and applying a displacement and a rotation so that it is transformed to {B}. If the initial superscript is missing we assume that the change in pose is relative to the world coordinate frame denoted O.
The point P in Fig. 2.2 can be described with respect to either coordinate frame.Formally we express this as
where the right-hand side expresses the motion from {A} to {B} and then to P. The operator · transforms the vector, resulting in a new vector that describes the same point but with respect to a different coordinate frame.
An important characteristic of relative poses is that they can be composed or compounded. Consider the case shown in Fig. 2.3. If one frame can be described in terms of another by a relative pose then they can be applied sequentially
which says, in words, that the pose of {C} relative to {A} can be obtained by compounding the relative poses from {A} to {B} and {B} to {C}. We use the operator ⊕ to indicate composition of relative poses.
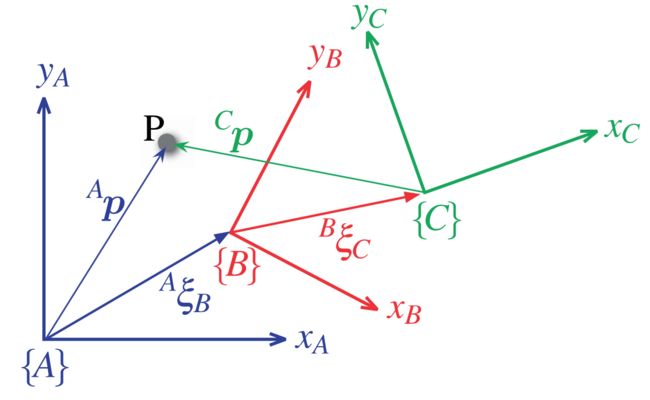
For this case the point P can be described
Later in this chapter we will convert these abstract notions of ξ, · and ⊕ into standard mathematical objects and operators that we can implement in MATLAB®.
In the examples so far we have shown 2-dimensional coordinate frames. This is appropriate for a large class of robotics problems, particularly for mobile robots which operate in a planar world. For other problems we require 3-dimensional coordinate frames to describe objects in our 3-dimensional world such as the pose of a flying or underwater robot or the end of a tool carried by a robot arm.
The point P can be described by coordinate vectors relative to either frame {A}, {B} or {C}. The frames are described by relative poses
In relative pose composition we can check that we have our reference frames correct by ensuring that the subscript and superscript on each side of the ⊕ operator are matched. We can then cancel out the intermediate subscripts and superscripts
leaving just the end most subscript and superscript which are shown highlighted.
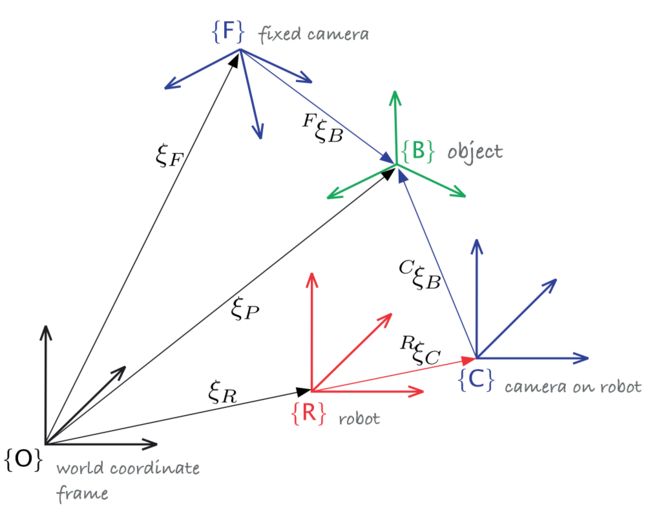
Figure 2.4 shows a more complex 3-dimensional example in a graphical form where we have attached 3D coordinate frames to the various entities and indicated some relative poses. The fixed camera observes the object from its fixed viewpoint and estimates the object’s pose relative to itself. The other camera is not fixed, it is attached to the robot at some constant relative pose and estimates the object’s pose relative to itself.
An alternative representation of the spatial relationships is a directed graph (see Appendix J) which is shown in Fig. 2.5. Each node in the graph represents a pose and each edge represents a relative pose. An arrow from X to Y is denoted XξY and describes the pose of Y relative to X. Recalling that we can compose relative poses using the ⊕ operator we can write some spatial relationships
and each equation represents a loop in the graph. Each side of the equation represents a path through the network, a sequence of edges (arrows) that are written in head to tail order. Both sides of the equation start and end at the same node.
A very useful property of poses is the ability to perform algebra.
In mathematical objects terms poses constitute a group – a set of objects that supports an associative binary operator (composition) whose result belongs to the group, an inverse operation and an identity element. In this case the group is the special Euclidean group in either 2 or 3 dimensions which are commonly referred to as SE(2) or SE(3) respectively.
The second loop equation says, in words, that the pose of the robot is the same as composing two relative poses: from the world frame to the fixed camera and from the fixed camera to the
René Descartes (1596–1650) was a French philosopher, mathematician and part-time mercenary. He is famous for the philosophical statement “Cogito, ergo sum” or “I am thinking, therefore I exist” or “I think, therefore I am”. He was a sickly child and developed a life-long habit of lying in bed and thinking until late morning. A possibly apocryphal story is that during one such morn- ing he was watching a fly walk across the ceiling and realized that he could describe its position in terms of its distance from the two edges of the ceiling. This coordinate system, the Cartesian system, forms the basis of modern (analytic) geometry and influenced the development of mod- ern calculus. In Sweden at the invitation of Queen Christine he was obliged to rise at 5 a.m., breaking his lifetime habit – he caught pneumonia and died. His remains were later moved to Paris, and then moved several times, and there is now some debate about where his remains are. After his death, the Roman Catholic Church placed his works on the Index of Prohibited Books.