Python高级--scipy图片处理+积分
导包
import numpy as np
import matplotlib.pyplot as plt
import scipy.misc as misc # 图片处理库 miscellaneous 乱七八糟一、黑白图片和彩色图片的区别
RGB图片
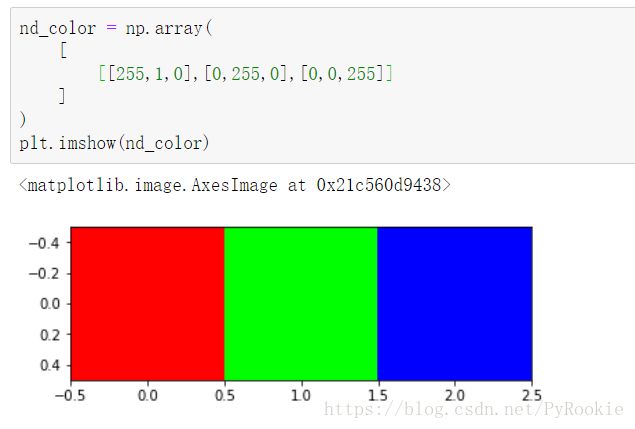
一般彩色图片由 plt.imread() 加载出来后是一个三维数组,一般最外维度是图片像素的行,中间维度是图片像素的列,最内层维度是图片的像素点(RGB)
nd_color = np.array(
[
[[255,1,0],[0,255,0],[0,0,255]] #最内层的RGB可以控制颜色
]
)
plt.imshow(nd_color)黑白图片
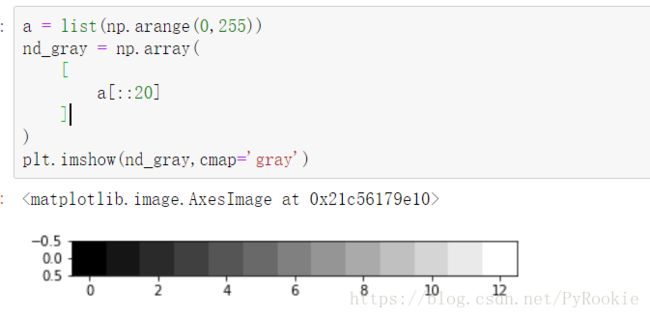
黑白图片由 plt.imread() 加载出来后是一个二维数组,没有最内层的像素点(RGB),只有从色到灰色。
a = list(np.arange(0,255))
#这里a为 [1,2,3,....,253,254,255]
nd_gray = np.array(
[
a[::20]
]
)
plt.imshow(nd_gray,cmap='gray')导入图片
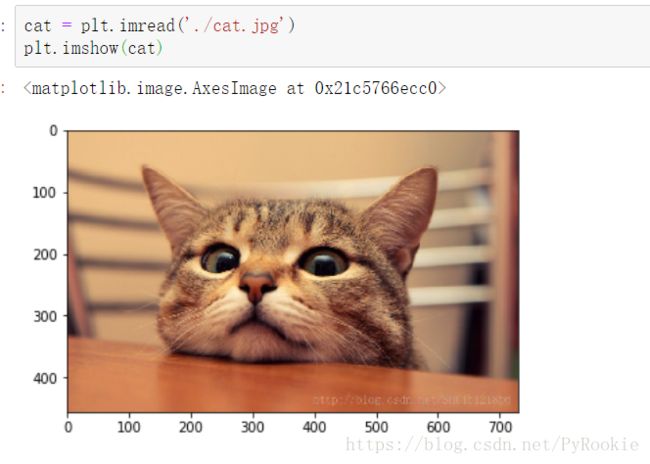
彩色图
cat = plt.imread('./cat.jpg')
cat.shape
(456, 730, 3) #可以看出彩色图片是三维数组黑白图
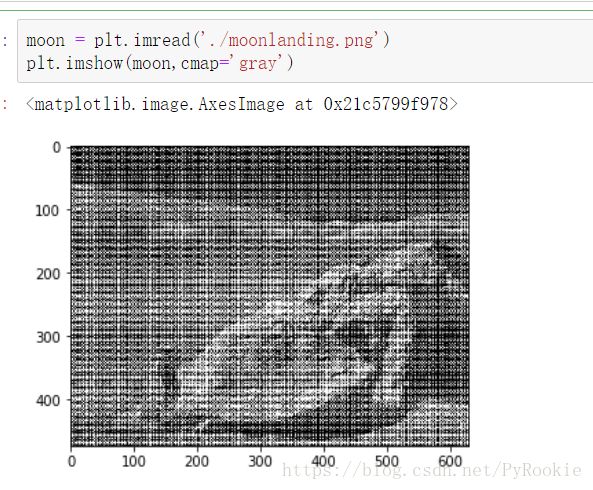
moon = plt.imread('./moonlanding.png')
moon.shape
(474, 630) #可以看出黑白图片是二维数组由此可见,彩色图片与黑白图片的差异是因为少一维度数据
图片的灰度处理
将彩色图片通过算法处理将最内层维度的[R,G,B]转换为一个值图片就成为了黑白图。
导入图片
cat = plt.imread('./cat.jpg') #将彩色图片加载为多维数组
cat
array([[[231, 186, 131], #此时是一个三维数组
[232, 187, 132],
...,
[188, 95, 62],
[188, 95, 62]]], dtype=uint8)
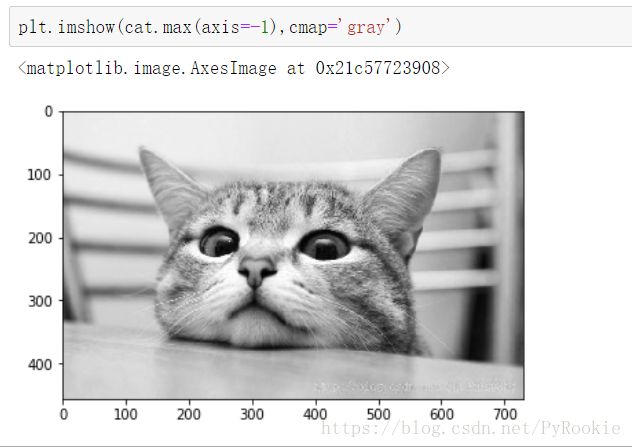
plt.imshow(cat) #将小猫的多维数组渲染展示1.取[R,G,B]的最大值
取小猫原始数据的最内层维度的最大值
cat.max(axis=-1)
array([[231, 232, 233, ..., 100, 92, 85], #转换后的数组是一个二维数组
[232, 232, 233, ..., 100, 92, 84],
...,
[199, 199, 199, ..., 188, 186, 188],
[199, 199, 199, ..., 188, 188, 188]], dtype=uint8)
plt.imshow(cat.max(axis=-1),cmap='gray') #将转换后的数组渲染出来cmap
cmap #colormap 颜色映射 matplotlib会自动将黑白图片作渲染,cmap=“gray”可以将默认的彩色渲染屏蔽掉,还原真实的黑白图片
cmap 还可以设置其他值,可以按Shift+Tab在map的参数里查看
2.取[R,G,B]的平均值
cat.mean(axis=-1)
array([[182.66666667, 183.66666667, 184.66666667, ..., 69.33333333,
62.33333333, 57.33333333],
...,
114.66666667, 115. ],
[133.33333333, 133.33333333, 133.33333333, ..., 116.66666667,
115. , 115. ]])
plt.imshow(cat.mean(axis=-1),cmap='gray') #将转换后的数组渲染出来3.取[R,G,B]的加权平均值(32:16:1)
根据人眼对光谱的敏锐程度来设置权重 [r:g:b] [0.64:0.35:0.01]
weight = np.array([0.64,0.35,0.01])
cat2 = np.dot(cat,weight) #对两个数组进行乘积就可以进行计算
plt.imshow(cat2,cmap="gray") #将转换好的数组渲染出来二、通过傅里叶变换实现图片降噪
1、傅里叶变换
傅里叶变换简单解释:把描述值的值 变成描述变化的值
导包
from scipy.fftpack import fft2,ifft2
'''
fft:first transform 快速傅里叶变换
fft2:把描述值的值 变成描述变化的值
ifft2:反傅里叶变化,将转换后的傅里叶变换指比较大的处理之后再变为描述值的值
'''数据:很久以前的月球表面照片
图片上的噪点是因为噪点的值与周围值变化太大展现出来的
moon = plt.imread('./moonlanding.png')
plt.imshow(moon,cmap='gray') # 傅里叶变换 把描述值的值 变成描述变化的值
fft2(moon) #j 复数我们只关注实数部分就行 # 值越大,说明变化越大
array([[126598.45 +0.j , -4608.5796 -1892.4688j ,
-322.093 -20.27744j , ..., -906.1585 +1539.3081j ,
-322.093 +20.27744j , -4608.5796 +1892.4688j ],
[ -9421.1 -5242.1133j , 1965.366 +2188.0593j ,
354.6247 +1003.8348j , ..., 1190.5856 -1431.9937j ,
1607.9927 -1269.4243j , 5224.016 +3171.7434j ]],
dtype=complex64)傅里叶变化处理噪声:
这里将变化(绝对值)大于2000的取出来让其归零
这里的2000的值可以依此来试进而得到最好的效果
fft_moon = fft2(moon) # 把描述值的值变成 描述变化的值
fft_moon[np.abs(fft_moon) > 2000] = 0 # 把变化大的 找出来 然后让变化归零
fft_moon
array([[ 0. +0.j , 0. +0.j ,
-322.093 -20.27744j , ..., -906.1585 +1539.3081j ,
-322.093 +20.27744j , 0. +0.j ],
[ 0. +0.j , 0. +0.j ,
0. +0.j , ..., -677.34503 -936.16174j ,
354.6247 -1003.8348j , 0. +0.j ],
,,,
[ 0. +0.j , 0. +0.j ,
354.6247 +1003.8348j , ..., 1190.5856 -1431.9937j ,
0. +0.j , 0. +0.j ]],
dtype=complex64)我们要将拿到的图片数据渲染出来
1)np.real(val)
功能:将数据中的复数过滤掉,只返回实数
2)plt.figure(num=None, figsize=None,)
功能:改变图片大小
figsize:(12,9)
设置渲染出来图片的尺寸3)plt.imsave(*args, **kwargs)
功能:保存渲染出来的图片
默认保存到当前目录
ifft_moon = np.real(ifft2(fft_moon)) # 处理之后 把描述变化的值 再恢复成描述值的值 #np.real取实数部分
plt.figure(figsize=(12,9)) #改变图片大小
plt.imshow(ifft_moon,cmap='gray') #渲染图片
plt.imsave('after.png',ifft_moon,cmap='gray') #保存图片 三、添加噪声
导入scipy.misc的自带图片
import matplotlib.pyplot as plt
import scipy.misc as misc #导包,重命名
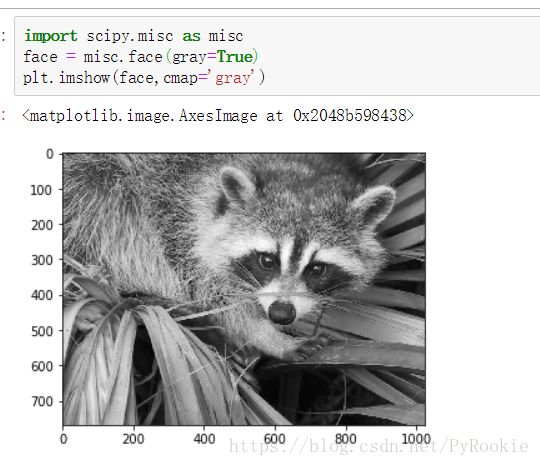
face = misc.face(gray=True) #使用scipy自带的图片 gray=True使图片为灰度图
plt.imshow(face,cmap='gray') 渲染出来添加噪声
原理:噪点的产生是因为原图片区域的数值变化过大产生的不规则的点,所以只要将原图片的数据进行不规则修改就可以产生噪点
face.shape #查看图片的形状
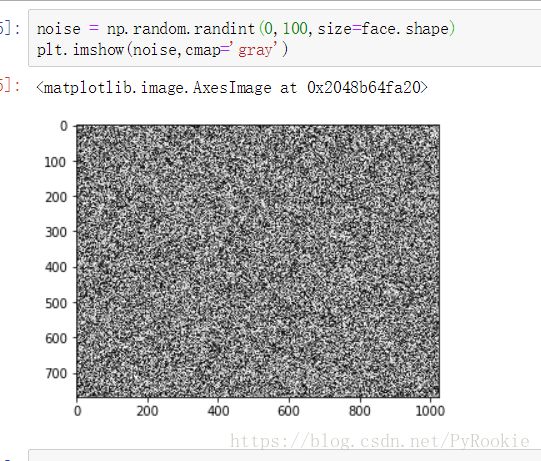
(768, 1024)noise = np.random.randint(0,100,size=face.shape)
array([[54, 67, 5, ..., 53, 0, 21],
[95, 79, 5, ..., 34, 88, 94],
[92, 90, 18, ..., 64, 53, 0],
...,
[83, 81, 86, ..., 99, 6, 24],
[68, 83, 73, ..., 46, 13, 38],
[61, 64, 38, ..., 73, 35, 1]])将噪声添加到图片
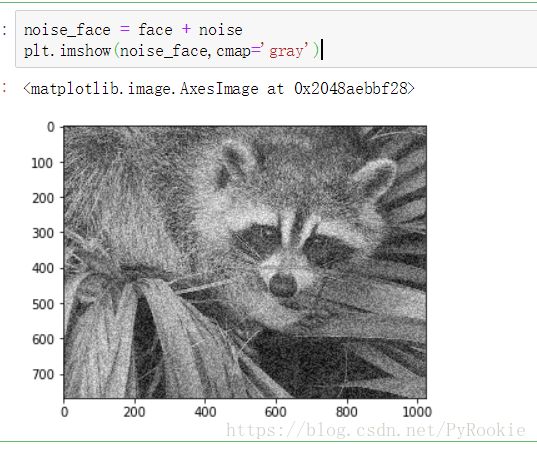
noise_face = face + noise #将随机生成的数据与原图片的数据相加就可以将噪点附加到原图片上。
plt.imshow(noise_face,cmap='gray')
四、scipy.ndimage(图像处理)处理噪声
原理:在图片数据中取一个范围,计算这个范围中的某些值(不同的滤波选取值的方式不同),平均值再和原来的值进行算法叠加,时原来的值向平均值趋近,使变化平缓,减小噪声
导入图像处理包:
import scipy.ndimage as ndimage #中值滤波,高斯滤波的包
from scipy.signal import wiener #维也纳滤波的包这里我们使用我们刚添加过噪声的浣熊图片做处理 noise_face
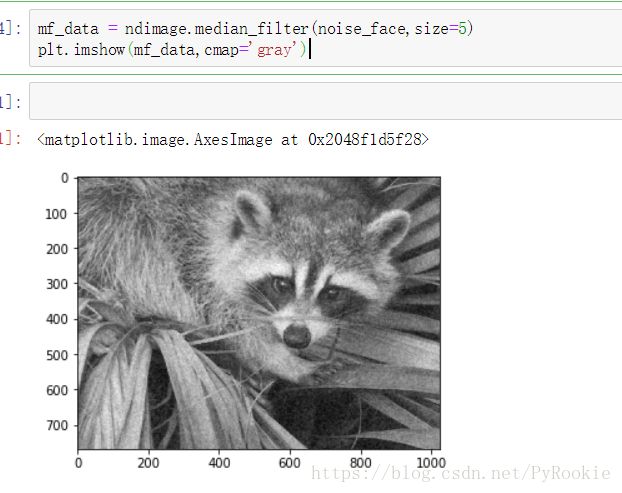
median中值滤波降噪
ndimage.median_filter(input,size=None)
'''
input:传入要处理的图片
size:设定了选取范围的大小(在实际处理的过程中对这个值要进行测试,来达到最好的效果)
'''
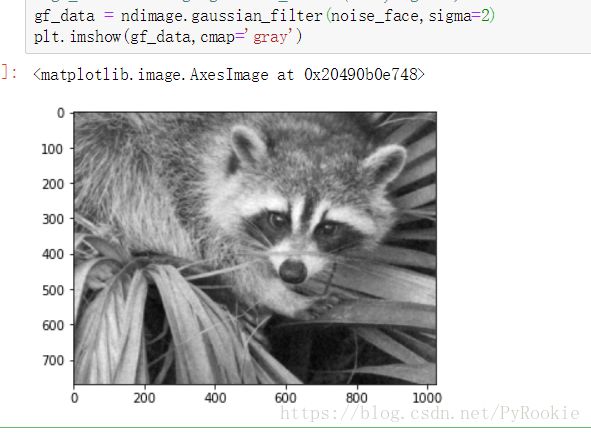
mf_data = ndimage.median_filter(noise_face,size=5)gaussian高斯滤波降噪
ndimage.gaussian_filter(input, sigma)
gf_data = ndimage.gaussian_filter(noise_face,sigma=2)
plt.imshow(gf_data,cmap='gray')signal维也纳滤波降噪
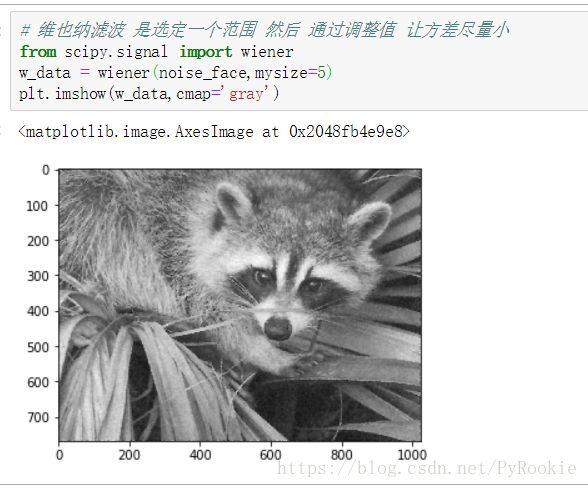
原理:在图片数据中取一个范围,计算这个范围中的平均值(不同的滤波选取值的方式不同),平均值再和原来的值进行方差计算,让方差尽量小,使变化平缓,减小噪声
from scipy.signal import wiener
w_data = wiener(noise_face,mysize=5)
plt.imshow(w_data,cmap='gray')图片处理效果总结
均值滤波 < 高斯滤波
高斯滤波(近景好) 维也纳滤波(远景好)
五、scipy.ndimage图片形状处理
处理数据:我们还是使用这个库自带的浣熊图片
import scipy.ndimage as ndimage
import scipy.misc
face = scipy.misc.face(gray=True)
face
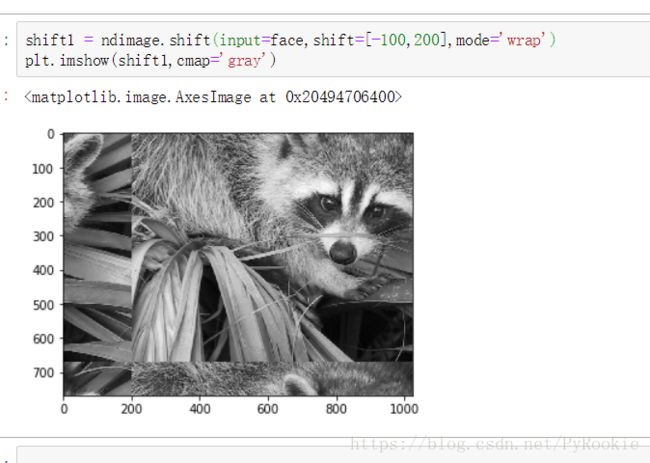
plt.imshow(face,cmap='gray')1.shift移动坐标
ndimage.shift(input,shift,output=None,order=3,mode=’constant’,cval=0.0,prefilter=True)
功能:将图片从原来的位置向制定的方向移动
'''
input:要处理的图片
shift:沿着坐标轴的位移
shift=100 先右,先下移动100像素
shift=[-100,200] 向上移动100,先右移动200
先上下,后左右
正数为 右下,负数为左上
mode:移动后填充的内容
{'reflect', 'constant', 'nearest', 'mirror', 'wrap'}
reflect:镜像填充
constant:由cval指定的值填充
nearest:有原图边缘的值填充
mirror:与reflect相同,镜像
wrap:输入通过绕到相反的边来扩展(折叠)
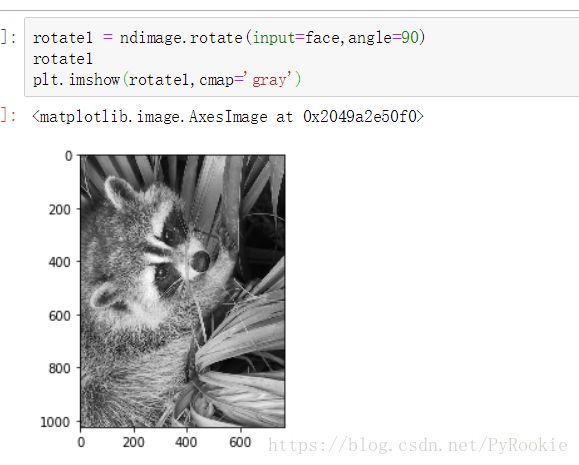
'''2.rotate旋转图片
ndimage.rotate(input,angle,axes=1,0),reshape=True,output=None,order=3,mode=’constant’,cval=0.0,prefilter=True)
'''
input:要旋转的矩阵
angle:旋转的角度
'''3.zoom缩放图片
ndimage.zoom(input,zoom,output=None,order=3,mode=’constant’,cval=0.0,prefilter=True)
'''
input:要缩放的矩阵
zoom:放大的倍数
zoom=2 矩阵放大一倍
zoom=[0.5,1] 上下缩小一倍,左右不变
zoom=[500/768,500/1024] 按比例缩放,缩放完之后的像素为500,500
mode:控制如何输入
'''4.切割图片(索引切片)
获取形状后对索引进行切片
'''
先行(先对样本切),后列(后对特征切)
'''
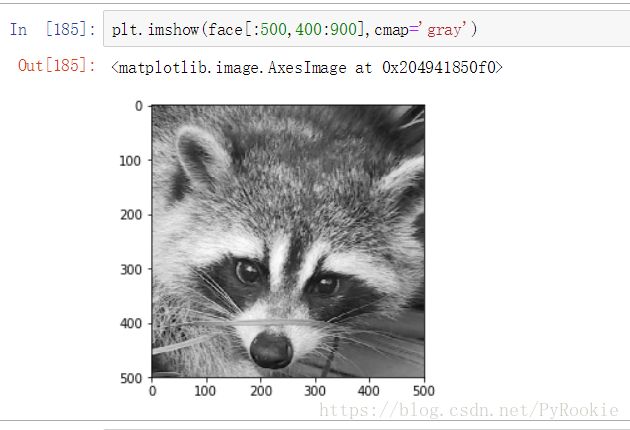
plt.imshow(face[:500,400:900],cmap='gray')图片练习
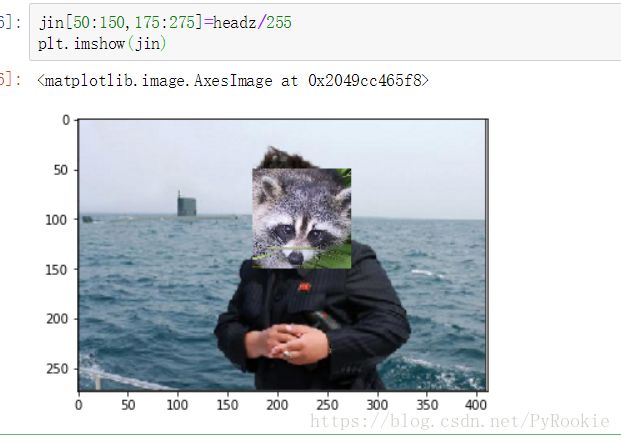
实现结果为
实现原理:截取小浣熊图片,并修改图片比例再将 金 图头像的位置替换为小浣熊比例转换后的图片

图片参数:
小浣熊使用scipy库中的图片
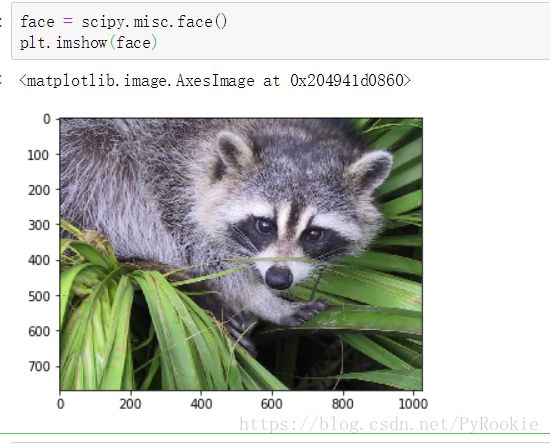
操作过程:
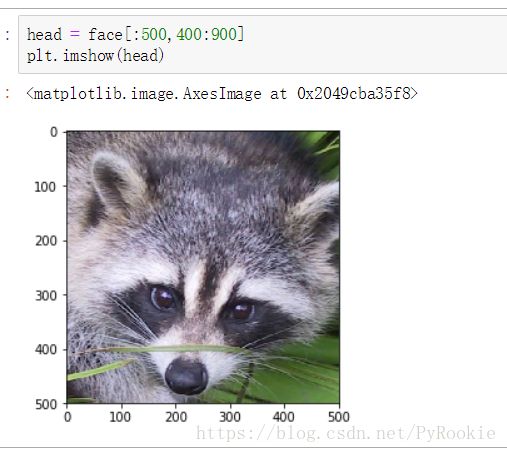
1.将小浣熊的头切割为 500*500像素的
head = face[:500,400:900]
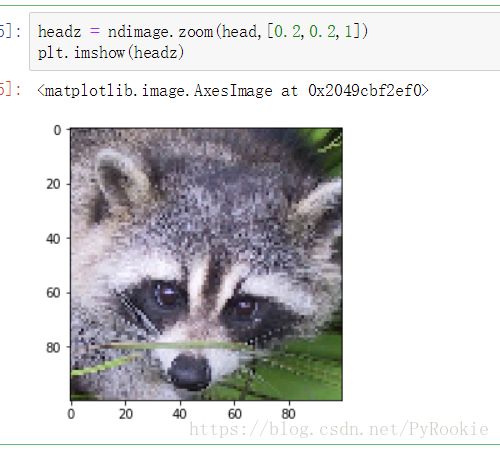
plt.imshow(head)2.将切割后的图片按比例缩小
headz = ndimage.zoom(head,[0.2,0.2,1])
plt.imshow(headz)3.将切割后的图片替换掉 金图片上的头
因为浣熊图片的值为0-255 所以要将其转换为0-1的
jin[50:150,175:275]=headz/255
plt.imshow(jin)利用积分求圆周率
积分原理:
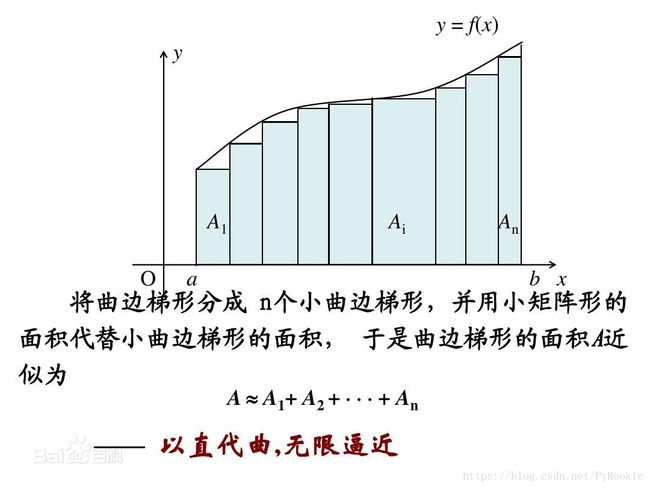
将要求的面积沿X轴分为n个小份,求处n小份的面积,最后将n个小面积加起来就近似为整个图形的面积
1. 推导并画出原
导包
import numpy as np
import pandas as pd
from pandas import Series,DataFrame
import matplotlib.pyplot as plt #pyplot 快速绘图工具
#直径为1的圆的公式的推导
# x**2 + y**2 = 1
# y**2 = 1 - x**2
# y = (1-x**2)**0.5
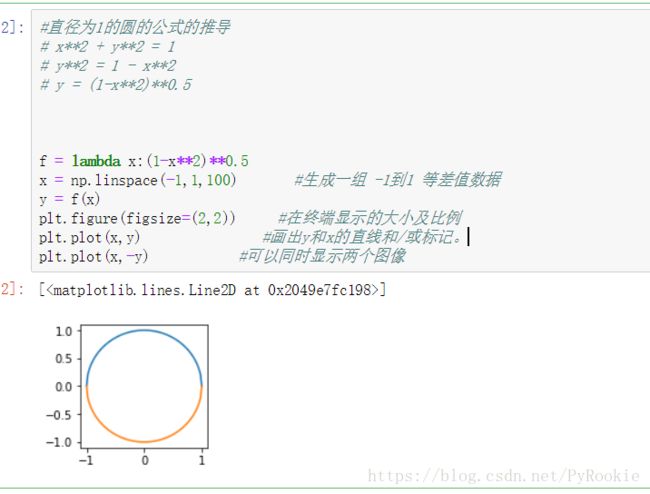
f = lambda x:(1-x**2)**0.5
x = np.linspace(-1,1,100) #生成一组 -1到1 等差值数据
y = f(x)
plt.figure(figsize=(2,2)) #在终端显示的大小及比例
plt.plot(x,y) #画出y和x的直线和/或标记。
plt.plot(x,-y) #可以同时显示两个图像2.使用scipy.integrate的quad()方法进行积分
导包
import scipy.integrate as integrate #integrate 求积分integrate.quad(func,a,b)
func: 对应关系(函数)
a,b: a是x轴的起始值, b是x轴的终止值
返回两个参数(运算结果,误差)res,error = integrate.quad(f,-1,1)
print('圆周率是:',res*2,'误差是:',error*2)
圆周率是: 3.141592653589797 误差是: 2.000471344132393e-09