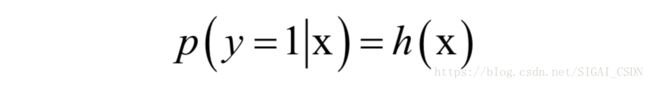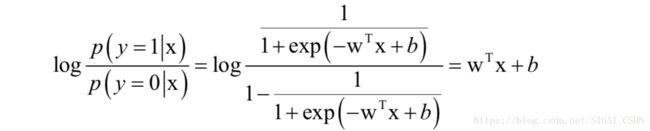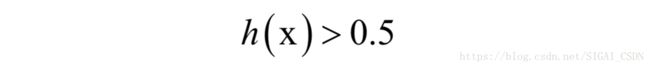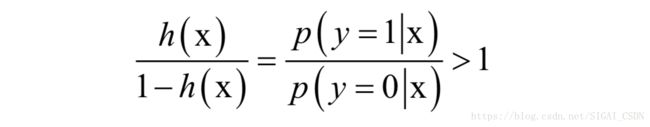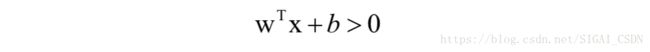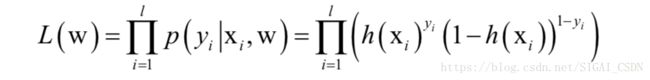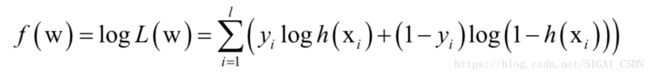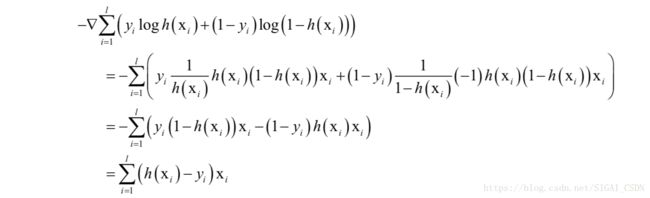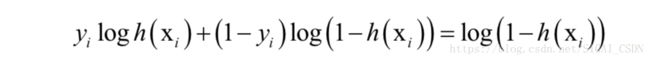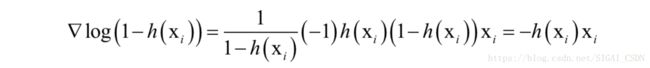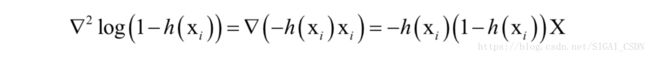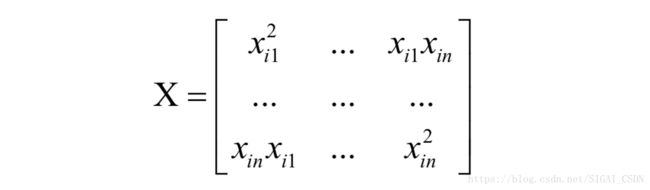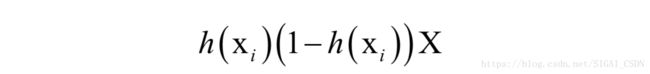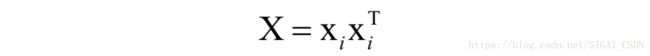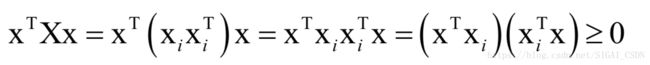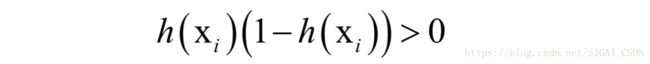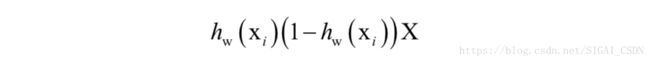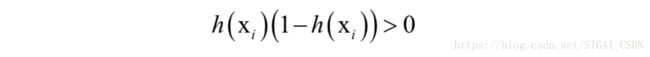理解 logistic 回归
其它机器学习、深度学习算法的全面系统讲解可以阅读《机器学习-原理、算法与应用》,清华大学出版社,雷明著,由SIGAI公众号作者倾力打造。
- 书的购买链接
- 书的勘误,优化,源代码资源
导言
logistic 回归是一种至今仍被广为使用的机器学习算法,虽然看似简单,但是很多人对它的认识存在某些误区,包括市面上的一些技术文章。在今天这篇文章中,SIGAI 将对 logistic回归的某些关键点进行阐述,帮助大家加深对这种算法的理解。
logistic回归简介
logistic回归由Cox在1958年提出[1],它的名字虽然叫回归,但这是一种二分类算法,并且是一种线性模型。由于是线性模型,因此在预测时计算简单,在某些大规模分类问题,如广告点击率预估(CTR)上得到了成功的应用。如果你的数据规模巨大,而且要求预测速度非常快,则非线性核的SVM、神经网络等非线性模型已经无法使用,此时logistic回归是你为数不多的选择。
直接预测样本属于正样本的概率
logistic回归源于一个非常朴素的想法:对于二分类问题,能否直接预测出一个样本 属于正样本的概率值?首先考虑最简单的情况,如果样本的输入向量 是一个标量 ,如何将它映射成一个概率值?我们知道,一个随机事件的概率p(a)必须满足两个条件:
概率值是非负的,即p(a)>=0
概率值不能大于1,即p(a)<=1这两个要求可以合并成,概率值必须在区间[0,1]内。在这里,样本的标签值为0或者1,分别代表负样本和正样本。将样本属于正样本这一事件记为p(y =1|x),即已知样本的特征向量值x,其标签值属于1的条件概率,也就是样本是正样本这一事件的概率。x的取值范围可以是(−∞ ,+∞ ),现在想想,哪些函数能够将一个(−∞ ,+∞ )之内的实数值变换到区间[0,1]?
考虑我们高中学过的基本函数,幂函数显然是不行的,当X→±∞的时候, 的值趋向于无穷大,而且有些幂函数的定义域不是(−∞ ,+∞ ),这就排除了所有的多项式函数。
直接使用指数函数也不行,当X→±∞时, 的值至少有一个会趋向于无穷大,无论a是正数还是负数。但指数函数有一个非常好的性质, 可以将(−∞ ,+∞ )内的数变换到(0,+∞ )内。通过它,也许可以构造出我们想要的函数。
对数函数显然也不行,因为它的定义域不是(−∞ ,+∞ ),因此直接被排除掉了,即使是用它来直接复合,也是不行的。
三角函数看似可以,比如正弦函数和余弦函数,可以将(−∞ ,+∞ )内的数压缩到[-1,1]之间,稍作变换,如使用 ,就可以将函数值压缩到[0,1] 之间。用三角函数进行复合,也许是可行的。
反三角函数显然不行,因为它的定义域不是(−∞ ,+∞ ),因此被直接排除了。
现在看来,基本的函数里,只有通过指数函数或三角函数,才有希望构造出我们想要的函数。但是,三角函数有一个问题:它是周期函数,在机器学习的很多应用中,我们显然不希望函数是周期性的,而应该是单调增或者单调减的。
最后我们再来想想指数函数,e^{x}可以将(−∞ ,+∞ )内的数变换到(0 ,+∞)内,我们在这个基础上很容易构造出一个值域为[0,1],并且单调增的函数。首先,得到一个(1 ,+∞ )内的数,然后取倒数即可。下面的函数就可以满足要求: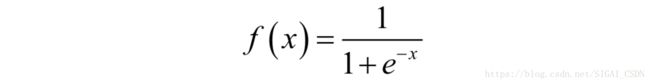
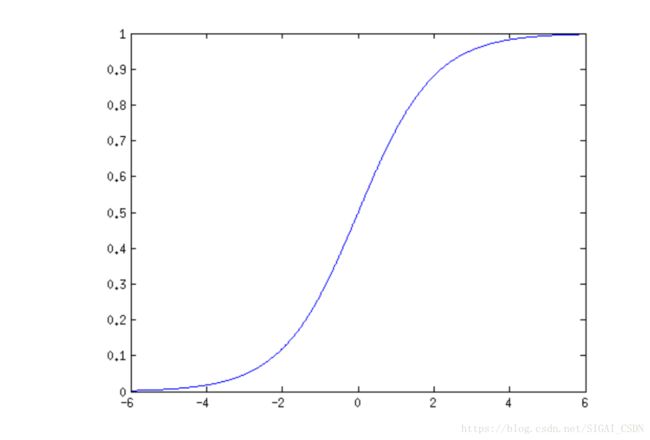
这就是机器学习中被广为使用的logistic函数,也叫sigmoid函数,它有一个迷人的性质,单调增,并且定义域是(−∞ ,+∞ ),值域是(0,1)(虽然不能取到0或者1,但这两个单独的点无关大局)。在神经网络的早期,也广泛的使用这个函数,SIGAI的logo也源自于这个函数。如果把它的图像画出来,是这样一条S曲线:
顺便说一句,不光机器学习使用它,S曲线也是很多女孩子梦寐以求的!现在看来,问题基本上解决了,我们已经找到了这样一个函数,输入一个样本的特征x,就可以得到一个(0,1)内的概率值,这就是样本属于正样本的概率。不过,之前我们假设样本的特征向量是一个标量,实际应用中不是这样的,它一般是一个向量。解决这个问题很简单,主要将向量映射成标量,然后带入logistic函数中继续预测就可以了。最简单的,可以使用线性映射如加权和:
写成向量形式为:
其中,w为权重向量,b为偏置项,是一个标量。至此,我们得到将一个样本的特征向量映射成一个概率值p(y =1|x)的函数:
这就是logistic回归的预测函数,至于怎样用这个映射函数做分类,接下来我们详细介绍。
对数似然比
根据前面的定义,一个样本属于正样本的概率为:
由于不是正样本就是负样本,因此属于负样本的概率为:
其中y为类别标签,取值为1或者0,分别对应正负样本。样本属于正样本和负样本概率值比的对数称为对数似然比:
按照常理,分类规则为,如果如果正样本的概率大于负样本的概率,即:
则样本被判定为正样本;否则被判定为负样本。而这等价于:
即:
也就是下面的线性不等式:
因此logistic回归是一个线性模型。在预测时,只需要计算上面这个线性函数的值,然后和0比较即可,而不需要用logistic函数进行映射,因为概率值大于0.5与上的值大于0是等价的。logistic函数映射只用于训练时。虽然用了非线性的logistic函数,但并不能改变logistic回归是一个线性分类器的本质,因为logistic函数是一个单调增函数。
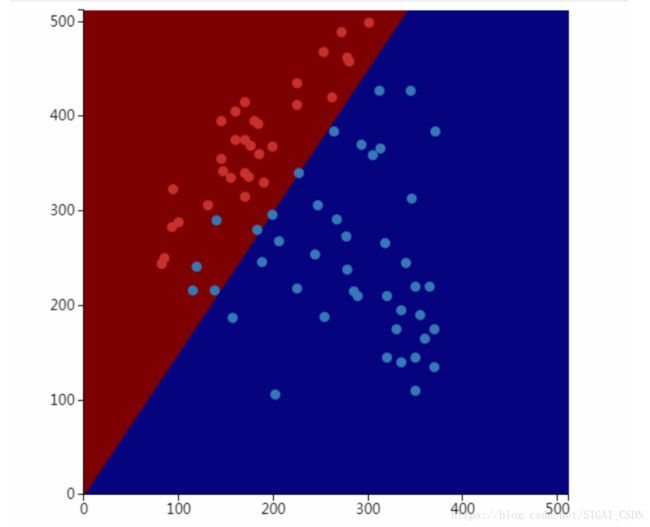
通过实验也可以直观的说明,logistic回归是一个线性模型。在这里,我们对红色和蓝色的圆点样本进行训练,得到模型,然后对整个图像上的点进行预测,得到每个像素的预测结果:
从图中可以看到,分界面是一条直线而不是曲线。上面的截图来自SIGAI云端实验室,登录我们的官网:
www.sigai.cn
注册账号之后即可使用,各种有趣的实验可以帮助更好的理解各种机器学习算法。
最大似然估计求解
前面介绍了logistic回归的预测函数与分类规则,接下来说明参数w和b是如何训练得到的。为了简化表述,在这里对向量进行扩充,将w和b合并成一个向量w,将向量x也扩充一维,其值固定为1,这样映射函数可以写成:
假设训练样本集为( , ),i=1,...,l,其中x_{i}是特征向量;y_{i}为类别标签,取值为1或0。给定参数w和样本特征向量x,样本属于每个类的概率可以统一写成如下形式:
证明很简单,令y为1和0,上式分别等于样本属于正负样本的概率。logistic回归预测的是样本属于某一类的概率,样本的类别标签为离散的1或者0,因此不适合直接用欧氏距离误差来定义损失函数,这里通过最大似然估计来确定参数。由于样本之间相互独立,训练样本集的似然函数为:
这个函数对应于n重伯努利分布。对数似然函数为:
要求该函数的最大值,等价于求解如下最小化问题:
可以使用梯度下降法求解,目标函数的梯度为:
最后得到权重的梯度下降法的迭代更新公式为:
除了梯度下降法这种一阶优化技术,还可以使用牛顿法及其变种,如BFGS算法。接下来我们会证明,上面的诱惑问题是凸优化,因此这些优化算法能保证收敛到全局最优解。如果你对凸优化和梯度下降法的原理还不清楚,可以阅读SIGAI之前的公众号文章“理解梯度下降法”,“理解凸优化”。
logistic回归是一个凸优化问题
下面我们来证明一个重要结论,logistic回归训练时优化的目标函数是凸函数。下面分两种情况进行证明。对于任何一个样本,如果y_{i} = 0即样本是负样本,有:
函数的梯度为:
这里利用了logistic函数的导数公式。函数的Hessian矩阵为:
如果单个样本的特征向量为x_{i} = ,..., ]T,令矩阵X为:
则−log(1−h(x_{i}))的Hessian矩阵为:
矩阵X可以写成如下乘积形式:
对任意不为0的向量X有:
从而矩阵X半正定,另外由于:
因此Hessian矩阵半正定,上面的函数是凸函数。下面考虑另外一种情况,如果y_{i} =1,则有:
Hessian矩阵为:
这里矩阵X的定义与前一种情况相同。因此−loghw (x_{i} )的Hessian矩阵为:
矩阵X是半正定矩阵,由于:
因此这个函数是凸函数。因为所有样本的:
都是凸函数,由于凸函数的非负线性组合还是凸函数,所以目标函数是凸函数,这个最优化问题是不带约束条件的凸优化问题。
下面同样通过实验来直观的说明这个问题是凸优化问题,我们来看训练时的损失函数曲线值:
从图中可以看出,梯度下降法每次迭代时函数值都下降,最后收敛到最优解。上图同样来自SIGAI云端实验室,感兴趣的读者可以自己去做实验。
总结
logistic回归是一种二分类算法,它用logistic函数预测出一个样本属于正样本的概率值。预测时,并不需要真的用logistic函数映射,而只需计算一个线性函数,因此是一种线性模型。训练时,采用了最大似然估计,优化的目标函数是一个凸函数,因此能保证收敛到全局最优解。虽然有概率值,但logistic回归是一种判别模型而不是生成模型,因为它并没有假设样本向量x所服从的概率分布,即没有对p(x, y)建模,而是直接预测类后验概率p(y|x)的值。
推广到多类
logistic回归只能用于二分类问题,将它进行推广可以得到处理多类分类问题的softmax回归,思路类似,采用指数函数进行变换,然后做归一化。这种变换在神经网络尤其是深度学习中被广为使用,对于多分类问题,神经网络的最后一层往往是softmax层(不考虑损失函数层,它只在训练时使用)。欲知softmax原理如何,且听下回分解!在文章的结尾,我们缅怀一下单田芳老爷子!笔者在帝都坐出租车,10次估计有3次司机是在放老爷子的评书。
参考文献
[1] Cox, DR (1958). The regression analysis of binary sequences (with discussion). J Roy Stat Soc B. 20 (2): 215–242.