OpenGL.Shader:9-学习光照-法线贴图(计算TBN矩阵)
OpenGL.Shader:9-学习光照-法线贴图(计算TBN矩阵)
这次文章学习法线贴图,法线贴图在游戏开发和GIS系统开发当中尤为广泛,其表现力特别的强,绘制的效果特别接近真实。更重要的一点就是,我们可以用很少的代价就可以制作出非常经济化的模型所表现的效果。这一点在游戏大作中尤为重要。
我们先来看看上方两个立方体贴图效果。左侧一方是普通的纹理贴图,右侧一方是法线贴图,两者视觉效果有巨大的差别,这就是法线贴图的魅力所在。
在show代码前,这里简述一下法线贴图的相关知识。
1、法线映射
在模拟光照效果的时候,是什么使表面被视为完全平坦的表面来照亮?答案就是表面的法线向量。以一块砖块为例子,以光照算法的角度,砖块表面只有一个法线向量,表面完全根据这个法线向量被以一致的方式照亮,所以细节效果的实现往往比较单一。如果每个片元都有自己的不同的法线会怎样?这样我们就可以根据表面细微的细节对法线向量进行改变;这样就会获得一种表面看起来要复杂得多的视觉效果:
每个片元都使用了自己的法线,我们就可以让一个表面由很多微小的(不同的法线向量的)平面所组成,这样的物体表面的细节将会得到极大提升。这种每个片元像素使用各自的法线,替代一个面上所有片元使用同一个法线的技术叫做法线映射(normal mapping)
由于法线向量是一个3元的几何模型,2D纹理不仅可以储存颜色和光照数据,还可以储存法线向量。思考一番,纹理中的颜色分量r、g、b用一个vec3的数学模型代表。同样是vec3的法线向量x、y、z元素也是能储存到纹理当中,代替颜色的r、g、b元素,组成一张法线纹理。这样我们就可以同时根据一组位置数据,从法线纹理中采样得到对应位置的法线向量。这样法线贴图就可以像纹理贴图一样工作了。
2、切线空间
既然我们把法线向量(x、y、z)映射到一张贴图纹理的(r、g、b)分量上,那么第一思维直觉,每个片元的法向量肯定是垂直于这个纹理所在的平面(即UV坐标组成的平面),三个分量的比重大部分都在z(b)分量上,所以的法线纹理多数就是呈现出偏蓝色的外观视觉。(如下图示)但是这样会有一个严峻的问题,在我们例子当中,正方体六个面,只有顶部面的法向量是(0,0,1),其他方向的面岂不是不能引用这张法线纹理?
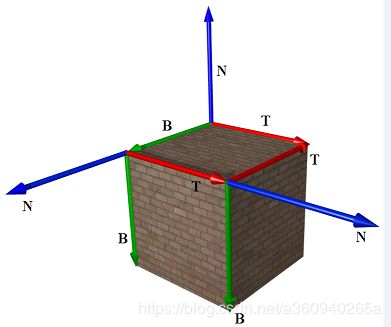
思考一下,我们是怎么把模型顶点/纹理坐标,转换成世界坐标?法向量是如何同步到模型的变化操作?都是通过坐标系的矩阵运算,这里引入切线空间(tangent space)坐标系。普通2维纹理坐标包含U、V两项,其中U坐标增长的方向, 即切线空间中的切线方向(tangent轴),V坐标增加的方向,为切线空间中的副切线方向(bitangent轴)模型中不同的面,都有对应的切线空间,其tangent轴和bitangent轴分别位于绘制的平面上,结合对应的法线方向,我们称tangant轴(T)、bitangent轴(B)及法线轴(N)所组成的坐标系,即切线空间(TBN)(如下图)
有了TBN切线空间坐标系,从法线纹理提取出的法向量,就是基于TBN的数值,然后我们再数学矩阵运算,乘以一个TBN转换矩阵,就可以正确的转换成模型所需要的正确方向的法线向量了。
(其中TBN矩阵的求法,更深层次的数学转换原理、请参考以下链接)
https://blog.csdn.net/jxw167/article/details/58671953
https://blog.csdn.net/yuchenwuhen/article/details/71055602
3、代码运用
class CubeTBN {
struct V3N3UV2 {
float x, y, z; //位置坐标
float nx, ny, nz; //法向量
float u,v; //纹理坐标
};
struct V3N3UV2TB6
{
float x, y, z;
float nx, ny, nz;
float u, v;
float tx,ty,tz;
float bx,by,bz;
};
// ...
};首先我们定义两个结构体,V3N3UV2就是我们之前一直使用的标准数据结构(位置顶点vec3,法向量vec3,纹理坐标vec2)。在V3N3UV2增加2个vec3,分别是切线方向(tangent轴)和副切线方向(bitangent轴)。通过方法convertTBN求出具体的数值
public:
V3N3UV2TB6 _data[36];
void init(const CELL::float3 &halfSize)
{
// 之前的标准数据,通过传入size确定大小。
V3N3UV2 verts[] =
{
// 前
{-halfSize.x, +halfSize.y, +halfSize.z, 0.0f, 0.0f, +1.0f, 0.0f,0.0f},
{-halfSize.x, -halfSize.y, +halfSize.z, 0.0f, 0.0f, +1.0f, 1.0f,0.0f},
{+halfSize.x, +halfSize.y, +halfSize.z, 0.0f, 0.0f, +1.0f, 0.0f,1.0f},
{-halfSize.x, -halfSize.y, +halfSize.z, 0.0f, 0.0f, +1.0f, 1.0f,0.0f},
{+halfSize.x, -halfSize.y, +halfSize.z, 0.0f, 0.0f, +1.0f, 1.0f,1.0f},
{+halfSize.x, +halfSize.y, +halfSize.z, 0.0f, 0.0f, +1.0f, 0.0f,1.0f},
// 后
{+halfSize.x, -halfSize.y, -halfSize.z, 0.0f, 0.0f, -1.0f, 1.0f,0.0f},
{-halfSize.x, -halfSize.y, -halfSize.z, 0.0f, 0.0f, -1.0f, 1.0f,1.0f},
{+halfSize.x, +halfSize.y, -halfSize.z, 0.0f, 0.0f, -1.0f, 0.0f,0.0f},
{-halfSize.x, +halfSize.y, -halfSize.z, 0.0f, 0.0f, -1.0f, 1.0f,0.0f},
{+halfSize.x, +halfSize.y, -halfSize.z, 0.0f, 0.0f, -1.0f, 0.0f,0.0f},
{-halfSize.x, -halfSize.y, -halfSize.z, 0.0f, 0.0f, -1.0f, 1.0f,1.0f},
// 左
{-halfSize.x, +halfSize.y, +halfSize.z, -1.0f, 0.0f, 0.0f, 0.0f,0.0f},
{-halfSize.x, -halfSize.y, -halfSize.z, -1.0f, 0.0f, 0.0f, 1.0f,1.0f},
{-halfSize.x, -halfSize.y, +halfSize.z, -1.0f, 0.0f, 0.0f, 1.0f,0.0f},
{-halfSize.x, +halfSize.y, -halfSize.z, -1.0f, 0.0f, 0.0f, 0.0f,1.0f},
{-halfSize.x, -halfSize.y, -halfSize.z, -1.0f, 0.0f, 0.0f, 1.0f,1.0f},
{-halfSize.x, +halfSize.y, +halfSize.z, -1.0f, 0.0f, 0.0f, 0.0f,0.0f},
// 右
{+halfSize.x, +halfSize.y, -halfSize.z, +1.0f, 0.0f, 0.0f, 0.0f,0.0f},
{+halfSize.x, +halfSize.y, +halfSize.z, +1.0f, 0.0f, 0.0f, 0.0f,1.0f},
{+halfSize.x, -halfSize.y, +halfSize.z, +1.0f, 0.0f, 0.0f, 1.0f,1.0f},
{+halfSize.x, -halfSize.y, -halfSize.z, +1.0f, 0.0f, 0.0f, 1.0f,0.0f},
{+halfSize.x, +halfSize.y, -halfSize.z, +1.0f, 0.0f, 0.0f, 0.0f,0.0f},
{+halfSize.x, -halfSize.y, +halfSize.z, +1.0f, 0.0f, 0.0f, 1.0f,1.0f},
// 上
{-halfSize.x, +halfSize.y, +halfSize.z, 0.0f, +1.0f, 0.0f, 0.0f,1.0f},
{+halfSize.x, +halfSize.y, +halfSize.z, 0.0f, +1.0f, 0.0f, 1.0f,1.0f},
{+halfSize.x, +halfSize.y, -halfSize.z, 0.0f, +1.0f, 0.0f, 1.0f,0.0f},
{-halfSize.x, +halfSize.y, -halfSize.z, 0.0f, +1.0f, 0.0f, 0.0f,0.0f},
{-halfSize.x, +halfSize.y, +halfSize.z, 0.0f, +1.0f, 0.0f, 0.0f,1.0f},
{+halfSize.x, +halfSize.y, -halfSize.z, 0.0f, +1.0f, 0.0f, 1.0f,0.0f},
// 下
{+halfSize.x, -halfSize.y, -halfSize.z, 0.0f, -1.0f, 0.0f, 1.0f,1.0f},
{+halfSize.x, -halfSize.y, +halfSize.z, 0.0f, -1.0f, 0.0f, 1.0f,0.0f},
{-halfSize.x, -halfSize.y, -halfSize.z, 0.0f, -1.0f, 0.0f, 0.0f,1.0f},
{+halfSize.x, -halfSize.y, +halfSize.z, 0.0f, -1.0f, 0.0f, 1.0f,0.0f},
{-halfSize.x, -halfSize.y, +halfSize.z, 0.0f, -1.0f, 0.0f, 0.0f,0.0f},
{-halfSize.x, -halfSize.y, -halfSize.z, 0.0f, -1.0f, 0.0f, 0.0f,1.0f}
};
// 根据位置/纹理 -> TBN
convertTBN(verts, _data);
}
void convertTBN(V3N3UV2* vertices,V3N3UV2TB6* nmVerts)
{
for (size_t i = 0; i <36; i += 3) // 一次操作一个三角形的三个点
{
// copy xyz normal uv
nmVerts[i + 0].x = vertices[i + 0].x;
nmVerts[i + 0].y = vertices[i + 0].y;
nmVerts[i + 0].z = vertices[i + 0].z;
nmVerts[i + 0].nx = vertices[i + 0].nx;
nmVerts[i + 0].ny = vertices[i + 0].ny;
nmVerts[i + 0].nz = vertices[i + 0].nz;
nmVerts[i + 0].u = vertices[i + 0].u;
nmVerts[i + 0].v = vertices[i + 0].v;
nmVerts[i + 1].x = vertices[i + 1].x;
nmVerts[i + 1].y = vertices[i + 1].y;
nmVerts[i + 1].z = vertices[i + 1].z;
nmVerts[i + 1].nx = vertices[i + 1].nx;
nmVerts[i + 1].ny = vertices[i + 1].ny;
nmVerts[i + 1].nz = vertices[i + 1].nz;
nmVerts[i + 1].u = vertices[i + 1].u;
nmVerts[i + 1].v = vertices[i + 1].v;
nmVerts[i + 2].x = vertices[i + 2].x;
nmVerts[i + 2].y = vertices[i + 2].y;
nmVerts[i + 2].z = vertices[i + 2].z;
nmVerts[i + 2].nx = vertices[i + 2].nx;
nmVerts[i + 2].ny = vertices[i + 2].ny;
nmVerts[i + 2].nz = vertices[i + 2].nz;
nmVerts[i + 2].u = vertices[i + 2].u;
nmVerts[i + 2].v = vertices[i + 2].v;
// Shortcuts for vertices
CELL::float3 v0 = CELL::float3(vertices[i + 0].x,vertices[i + 0].y,vertices[i + 0].z);
CELL::float3 v1 = CELL::float3(vertices[i + 1].x,vertices[i + 1].y,vertices[i + 1].z);
CELL::float3 v2 = CELL::float3(vertices[i + 2].x,vertices[i + 2].y,vertices[i + 2].z);
CELL::float2 uv0 = CELL::float2(vertices[i + 0].u, vertices[i + 0].v);
CELL::float2 uv1 = CELL::float2(vertices[i + 1].u, vertices[i + 1].v);
CELL::float2 uv2 = CELL::float2(vertices[i + 2].u, vertices[i + 2].v);
// 构建triangle平面的方向向量 (position delta, δ)
CELL::float3 deltaPos1 = v1 - v0;
CELL::float3 deltaPos2 = v2 - v0;
// 构建UV平面的两个方向的向量 (uv delta, δ)
CELL::float2 deltaUV1 = uv1 - uv0;
CELL::float2 deltaUV2 = uv2 - uv0;
float r = 1.0f / (deltaUV1.x * deltaUV2.y - deltaUV1.y * deltaUV2.x); // uv叉积作底
CELL::float3 tangent = (deltaPos1 * deltaUV2.y - deltaPos2 * deltaUV1.y)*r; // 得出切线
CELL::float3 binormal = (deltaPos2 * deltaUV1.x - deltaPos1 * deltaUV2.x)*r; // 得出副切线
// 赋值到t b
nmVerts[i + 0].tx = tangent.x; nmVerts[i + 0].bx = binormal.x;
nmVerts[i + 0].ty = tangent.y; nmVerts[i + 0].by = binormal.y;
nmVerts[i + 0].tz = tangent.z; nmVerts[i + 0].bz = binormal.z;
nmVerts[i + 1].tx = tangent.x; nmVerts[i + 1].bx = binormal.x;
nmVerts[i + 1].ty = tangent.y; nmVerts[i + 1].by = binormal.y;
nmVerts[i + 1].tz = tangent.z; nmVerts[i + 1].bz = binormal.z;
nmVerts[i + 2].tx = tangent.x; nmVerts[i + 2].bx = binormal.x;
nmVerts[i + 2].ty = tangent.y; nmVerts[i + 2].by = binormal.y;
nmVerts[i + 2].tz = tangent.z; nmVerts[i + 2].bz = binormal.z;
}
}至此,每个基准点的TBN矩阵都计算出来了。有了数据之后,我们就可以开始学习着色器程序的编写。
首先我们来看顶点着色器部分:
#version 320 es
in vec3 _position; // 外部输入
in vec3 _normal;
in vec2 _uv;
in vec3 _tagent;
in vec3 _biTagent;
uniform mat4 _mvp; // mvp矩阵
uniform mat3 _normalMatrix; // 法线矩阵
uniform mat4 _matModel; // 模型转换矩阵
out vec2 _outUV;
out vec3 _outPos;
out mat3 _TBN;
void main()
{
_outUV = _uv; //// 输出纹理坐标到片元着色器,用于提取纹理贴图和法线贴图
vec4 pos = _matModel*vec4(_position,1);
_outPos = pos.xyz; //// 输出模型顶点位置,保证每个片元都有细化的光照方向
vec3 normal = normalize(_normalMatrix * _normal); // 乘以法线矩阵,以保证模型变换操作后的一致性。
vec3 tagent = normalize(_normalMatrix * _tagent);
vec3 biTagent= normalize(_normalMatrix * _biTagent);
_TBN = mat3x3(tagent,biTagent,normal); // 构建TBN矩阵 输出到片元着色器
gl_Position = _mvp * vec4(_position,1.0); // 输出最终绘制的顶点坐标
}
em... 该说的都已经加注释了。 至于为什么要把模型化操作后的(世界坐标系的)顶点输出到片元着色器?计算光强度的主要属性——光照方向,之前我们都是直接在顶点着色器完成,这是因为之前我们没有掌握法线贴图这一重点内容,没能把法线向量细化到每个片元当中。顶点位置数据从顶点着色器输出到达片元着色器之后,片元着色器都会进行插值运算。插值之后,每个片元都有插值后的顶点位置数据,这样一来就要重新计算更为细化的光照方向,以配合法线贴图进行更好的计算效果。
#version 320 es
precision mediump float;
in vec2 _outUV;
in vec3 _outPos;
in mat3 _TBN;
uniform vec3 _lightColor;
uniform vec3 _lightDiffuse;
uniform sampler2D _texture;
uniform sampler2D _texNormal;
uniform vec3 _lightPos;
uniform vec3 _cameraPos;
out vec3 _fragColor;
void main()
{
vec3 lightDir = normalize(_lightPos - _outPos); // 计算每个片元属于自己的 光照方向
vec3 normal = normalize(_TBN * (texture(_texNormal,_outUV).xyz*2.0 - 1.0));
// 从法线贴图提取法向量 归一化[-1,1]区间 然后 通过TBN矩阵 转化为最终法向量
vec4 materialColor = texture(_texture,_outUV);
float lightStrength = max(dot(normal, lightDir), 0.0); // 计算光照强度
vec4 lightColor = vec4(_lightColor * lightStrength + _lightDiffuse, 1); // 光照强度*颜色光 + 漫反射光
_fragColor.rgb = materialColor.rgb * 0.2 + 0.8 * lightColor.rgb; // 混合输入效果。
}
_uv 纹理坐标提取纹理贴图的颜色值,又能提取法线贴图的法向量值。需要注意的是,texture(_texNormal,_outUV).xyz的范围值是[0,255],归一化是[0,1]。但是我们法向量需要的是[-1, 1],我们需要自己转换。最后混合输出效果不固定。大家按需调整效果就好。
最后加上CubeTBN.render方法。
void render(Camera3D& camera)
{
_program.begin();
static float angle = 0;
angle += 0.1f;
CELL::matrix4 matRot;
matRot.rotateYXZ(angle, 0.0f, 0.0f);
CELL::matrix4 model = _modelMatrix * matRot;
glUniformMatrix4fv(_program._matModel, 1, GL_FALSE, model.data());
CELL::matrix4 vp = camera.getProject() * camera.getView();
CELL::matrix4 mvp = (vp * model);
glUniformMatrix4fv(_program._mvp, 1, GL_FALSE, mvp.data());
CELL::matrix3 matNormal = mat4_to_mat3(model)._inverse()._transpose();
glUniformMatrix3fv(_program._normalMatrix, 1, GL_FALSE, matNormal.data());
glUniform3f(_program._lightDiffuse, 0.1f, 0.1f, 0.1f); // 漫反射 环境光
glUniform3f(_program._lightColor, 1.0f, 1.0f, 1.0f); // 定向光源的颜色
glUniform3f(_program._lightPos, camera._eye.x, camera._eye.y, camera._eye.z);//光源位置
glActiveTexture(GL_TEXTURE0);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D, _texMaterial);
glUniform1i(_program._texture, 0); // 加载纹理贴图
glActiveTexture(GL_TEXTURE1);
glEnable(GL_TEXTURE_2D);
glBindTexture(GL_TEXTURE_2D, _texNormal);
glUniform1i(_program._texNormal, 1); // 加载法线贴图
glVertexAttribPointer(_program._position, 3, GL_FLOAT, GL_FALSE, sizeof(V3N3UV2TB6), _data);
glVertexAttribPointer(_program._normal, 3, GL_FLOAT, GL_FALSE, sizeof(V3N3UV2TB6), &_data[0].nx);
glVertexAttribPointer(_program._uv, 2, GL_FLOAT, GL_FALSE, sizeof(V3N3UV2TB6), &_data[0].u);
glVertexAttribPointer(_program._tagent, 3, GL_FLOAT, GL_FALSE, sizeof(V3N3UV2TB6), &_data[0].tx);
glVertexAttribPointer(_program._biTagent, 3, GL_FLOAT, GL_FALSE, sizeof(V3N3UV2TB6), &_data[0].bx);
glDrawArrays(GL_TRIANGLES, 0, 36);
_program.end();
}工程demo源码:参考文件CubeTBN.hpp CubeTbnProgram.hpp
https://github.com/MrZhaozhirong/NativeCppApp