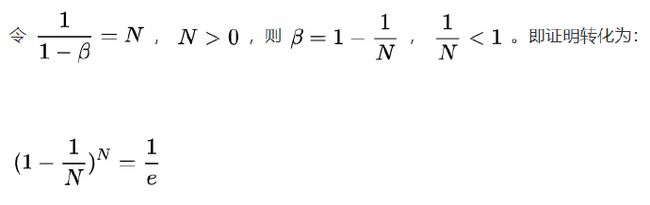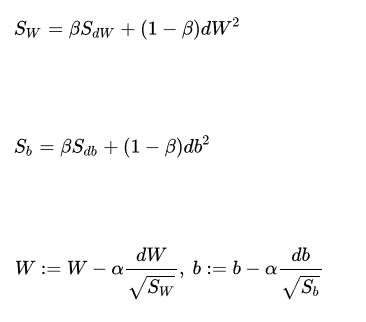【深度学习】梯度下降优化算法
随机性(方差)->噪声->波动大小
传统方法
https://www.jiqizhixin.com/articles/2016-11-21-4
batch批训练—不同的更新梯度的方式
batch梯度下降分为三种:batch梯度下降、随机化batch梯度下降、mini-batch梯度下降
1.batch
遍历全部数据集算一次损失函数,然后算函数对各个参数的梯度,更新梯度。这种方法每更新一次参数都要把数据集里的所有样本都看一遍
每次迭代,成本函数都会减小

2.随机化batch
每一个数据都计算一次损失函数,然后求梯度更新参数

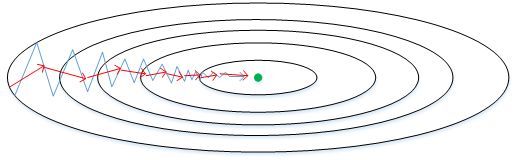
每次只对一个样本进行训练,cost不是单调下降,而是受类似噪声的影响,出现振荡。但整体的趋势是下降的,最终也能得到较低的cost值。
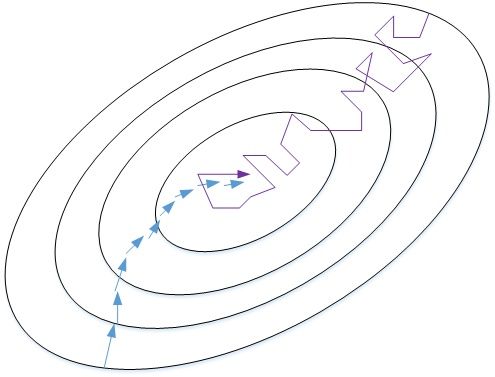
成本函数轮廓图
3.mini-batch梯度下降
把m个训练样本分成若干个子集,称为mini-batches,然后每次在单一子集上进行神经网络训练。这样,一个批中的一组数据共同决定了本次梯度的方向,下降起来就不容易跑偏,减少了随机性。另一方面因为一批的样本数与整个数据集相比小了很多,计算量也不是很大
假如有50万个训练集,每个mini-batch包括1000个样本,总共500个mini-batches。使用 batch 梯度下降法,一个mini-batch只做一次梯度下降。则只需要进行500次梯度下降即可。

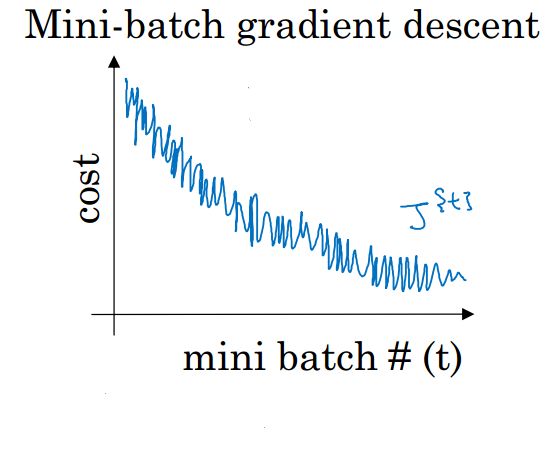
1.噪声
2.代价函数并不是单调较小的,不能精准收敛到最小值,只是在最小值附近波动。
mini-batch梯度下降优化-Learning rate decay
随时间慢慢减少学习率,我们将之称为学习率衰减。
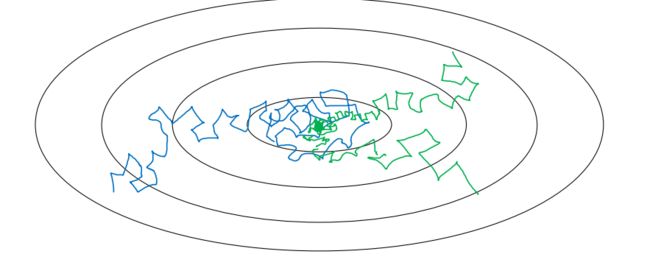
上图中,蓝色折线表示使用恒定的学习率 ,由于每次训练 学习率相同,步进长度不变,在接近最小值处的振荡也大,在最小值附近较大范围内振荡,与最小值距离就比较远。
绿色折线表示使用不断减小的 学习率,随着训练次数增加, 学习率逐渐减小,步进长度减小,使得能够在最小值处较小范围内微弱振荡,不断逼近最小值。相比较恒定的 学习率来说,learning rate decay更接近最小值。
常用的公式有:

其中,decay_rate是参数(可调),epoch是已训练样本集的次数。随着epoch增加, 学习率会不断变小。
总结:
1.如果训练集较小(小于 2000 个样本),直接使用 batch 梯度下降法
2.一般的 mini-batch 大小为 64 到 512,而且如果 mini-batch 大小是 2 的n次方,代码运行会快些
(因为计算机存储数据一般是2的幂,这样设置可以提高运算速度)
使用上述梯度下降算法时面临的挑战:
-
很难选择出合适的学习率。太小的学习率会导致网络收敛过于缓慢,而学习率太大可能会影响收敛,并导致损失函数在最小值上波动,甚至出现梯度发散。
-
此外,相同的学习率并不适用于所有的参数更新。如果训练集数据稀疏,且特征频率非常不同,则不应该将其全部更新到相同的程度,但是对于很少出现的特征,应使用更大的学习率。
-
非凸的损失函数优化过程存在大量的局部最小值或鞍点
优化方法
指数加权平均数(背景知识1)
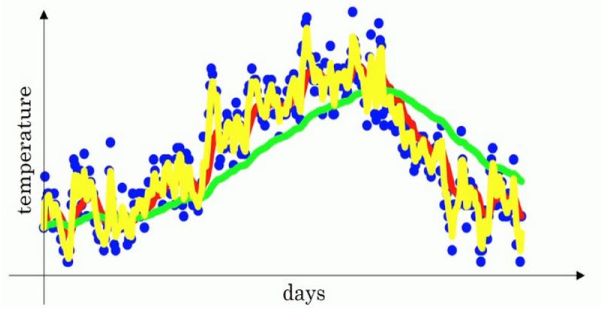
某个地区半年内的温度变化如下图所示:

我们可以用指数加权平均的关键函数来模拟温度变化的趋势。函数:
![]()
t天的平均温度不仅与当天数据相关,还与之前t-1的平均温度相关。
展开:
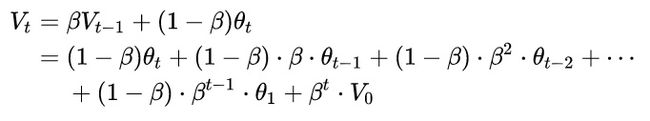
系数代表所对应数据对vt的影响程度,系数越大,影响越大。系数的分布类似一个指数衰减函数。
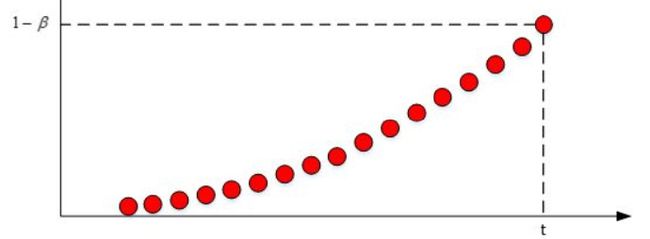
系数在不断衰减,当衰减到一定程度时,我们认为这个数据对vt的影响忽略不计。这个界限定为峰值的1/e.即可表示为:
β t = 1 e \beta^{t}=\frac{1}{e} βt=e1
t = 1 1 − β t=\frac{1}{1-\beta} t=1−β1, t代表指数加权平均的天数
当 β \beta β=0.9时,1/(1- β \beta β)等于10,也就是说要算某天的温度只需要关注过去10天的温度即可。
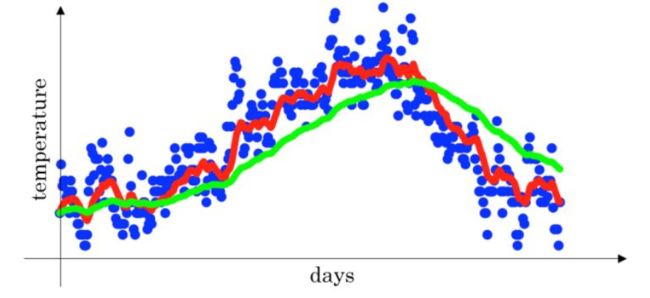
黄线: β \beta β=0.5
红线: β \beta β=0.9
绿线: β \beta β=0.98
实现算法:

指数加权平均数公式的好处之一在于,它只占用一行代码,计算指数加权平均数也只占用单行数字的存储和内存,占用内存极少。
在数据量非常大的情况下,指数加权平均在节约计算成本的方面是一种非常有效的方式,可以很大程度上减少计算机资源存储和内存的占用。
####偏差修正(背景知识二)
图中绿色线条和紫色线条 β \beta β都为0.98,紫色为不使用偏差修正的结果。区别在于紫色曲线开始的时候相对较低一些。
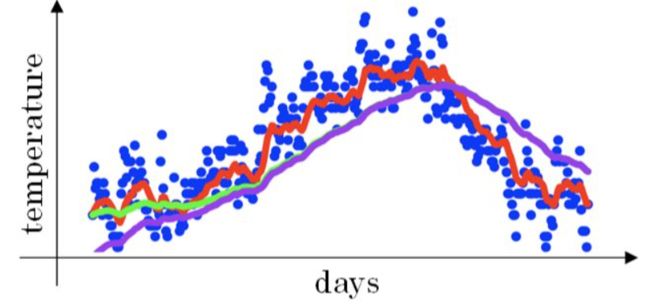
偏移修正(bias correction),即在每次计算完 vt后,再进行进行下式处理:
v t 1 − β t \frac{v_{t}}{1-\beta^{t}} 1−βtvt
在刚开始的时候,t比较小,这样就将 v t v_{t} vt 修正得更大一些,效果是把紫色曲线开始部分向上提升一些,与绿色曲线接近重合。随着t增大, 1 − β t 1-\beta^{t} 1−βt越来越接近1 ,紫色曲线与绿色曲线几乎重合。这样就实现了简单的偏移校正,得到我们希望的绿色曲线。
动量梯度下降法(Gradient descent with Momentum)(平均)
每次训练时,先计算梯度的指数加权平均数,然后用得到的梯度值更新参数。
图中的上下波动减慢了梯度下降法的速度。
同时也无法使用更大的学习率,如果用较大的学习率,结果可能会偏离函数的范围
思路:纵轴方向减小震荡,横轴方向学习速度加快。(优化相关方向的训练和弱化无关方向的振荡,来加速SGD训练)

原始的梯度下降算法如上图蓝色折线所示。在梯度下降过程中,梯度下降的振荡较大。此时每一点处的梯度只与当前方向有关,产生类似折线的效果,前进缓慢。而如果对梯度进行指数加权平均,这样使当前梯度不仅与当前方向有关,还与之前的方向有关,这样处理减小随机性,让梯度前进方向更加平滑,减少振荡,能够更快地到达最小值处。
这里的动量与经典物理学中的动量是一致的,就像从山上投出一个球,在下落过程中收集动量,小球的速度不断增加。
以权重W为例, $V_{dW} $可以成速度V, dW 可以看成是加速度a。指数加权平均实际上是计算当前的速度,当前速度由之前的速度和现在的加速度共同影响。而 β < 1 \beta<1 β<1 ,又能限制速度 V d W 过 大 V_{dW} 过大 VdW过大。也就是说,当前的速度是渐变的,而不是瞬变的,是动量的过程。这保证了梯度下降的平稳性和准确性,减少振荡,较快地达到最小值处。
动量梯度下降算法的过程如下:
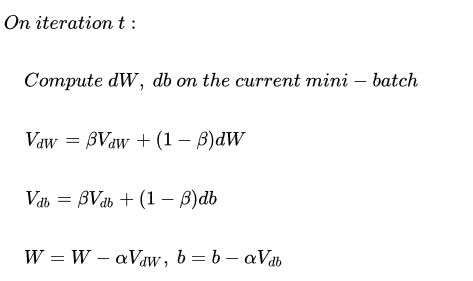
初始时,令 v d w = 0 , v d b = 0 v_{dw}=0,v_{db}=0 vdw=0,vdb=0。一般设置 β = 0.9 \beta=0.9 β=0.9,即指数加权平均前10次的数据,实际应用效果较好。
另外,关于偏移校正,可以不使用。因为经过10次迭代后,偏移情况会逐渐消失。
###RMSprop(方差)
RMSprop是另外一种优化梯度下降速度的算法,是对Adagrad算法的改进,解决其学习率不断较小最终达到一个非常小的值,模型学习速度很慢的问题。
Adagrad是一个基于梯度的优化算法。在这之前,我们对于所有的参数使用相同的学习率进行更新。但 Adagrad 则不然,Adagrad方法基于每个参数计算的过往梯度,为不同参数θ设置不同的学习率,不用手动调节学习率。
具体而言,对稀疏参数进行大幅更新和对频繁参数进行小幅更新(更新快一些对于不经常出现的特征,对于常出现的特征更新慢一些),因此,他很适合于处理稀疏数据。
从图中可以看出,梯度下降(蓝色折线)在垂直方向(b)上振荡较大,在水平方向(W)上振荡较小,表示在b方向上梯度较大,即 db 较大,而在W方向上梯度较小,即 dW 较小。因此,上述表达式中 S b S_b Sb 较大,而 $S_W 较 小 。 在 更 新 W 和 b 的 表 达 式 中 , 变 化 值 较小。在更新W和b的表达式中,变化值 较小。在更新W和b的表达式中,变化值 \frac{dW}{\sqrt{S_W}} $较大,而 d b S b \frac{db}{\sqrt{S_b}} Sbdb 较小。也就使得W变化得多一些,b变化得少一些。即加快了W方向的速度,减小了b方向的速度,减小振荡,实现快速梯度下降算法,其梯度下降过程如绿色折线所示。总得来说,就是如果哪个方向振荡大,就减小该方向的更新速度,从而减小振荡。
为了避免RMSprop算法中分母为零,通常可以在分母增加一个极小的数 ε \varepsilon ε
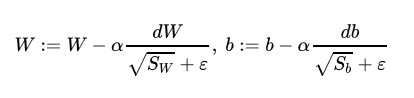
ε \varepsilon ε一般为 1 0 − 8 10^{-8} 10−8
###Adam
Adam(Adaptive Moment Estimation)算法结合了动量梯度下降算法和RMSprop算法,可视为带有动量项的RMSprop。
动量梯度下降算法和RMSprop算法的优点是:允许你使用一个更大的学习率,从而加快你的算法学习速度。同时RMSprop算法为不同的参数计算不同的自适应学习率
其算法流程为:

Adam算法包含了几个超参数, β 1 \beta1 β1 通常设置为0.9, β 2 \beta2 β2 通常设置为0.999, ε \varepsilon ε一般为 1 0 − 8 10^{-8} 10−8
特点:
结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
对内存需求较小
为不同的参数计算不同的自适应学习率
也适用于大多非凸优化 - 适用于大数据集和高维空间

补充:
稀疏数据:数据框中绝大多数数值缺失或者为零的数据
对于稀疏数据,尽量使用学习率可自适应的优化方法,不用手动调节,而且最好采用默认值 .
如果训练集数据很稀疏,且特征频率非常不同,则不应该将其全部更新到相同的程度,但是对于很少出现的特征,应使用更大的更新率。
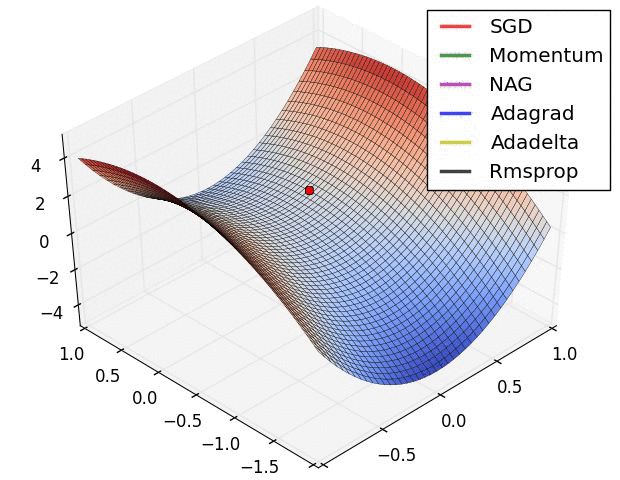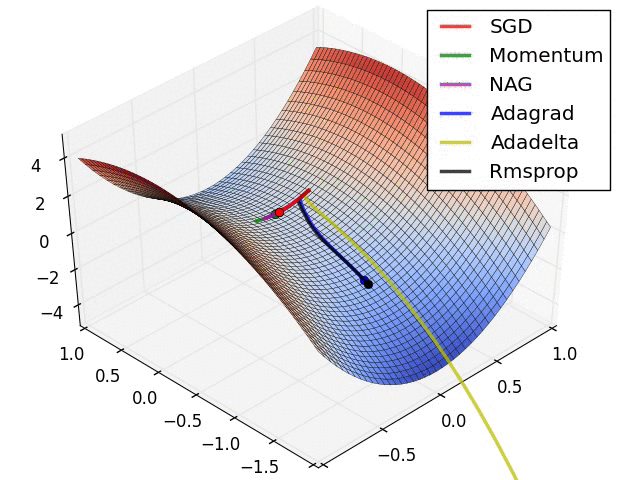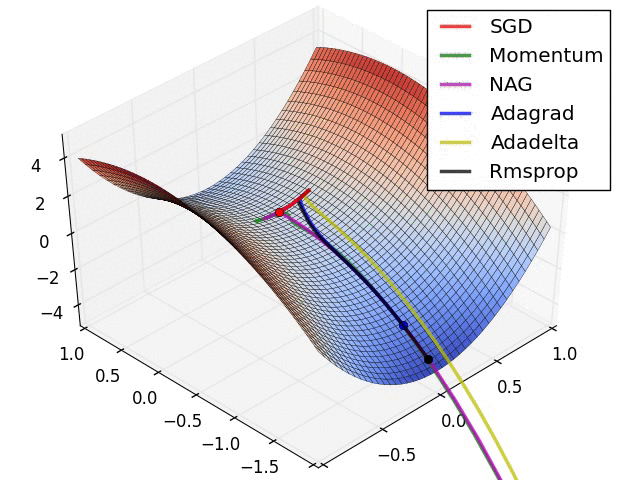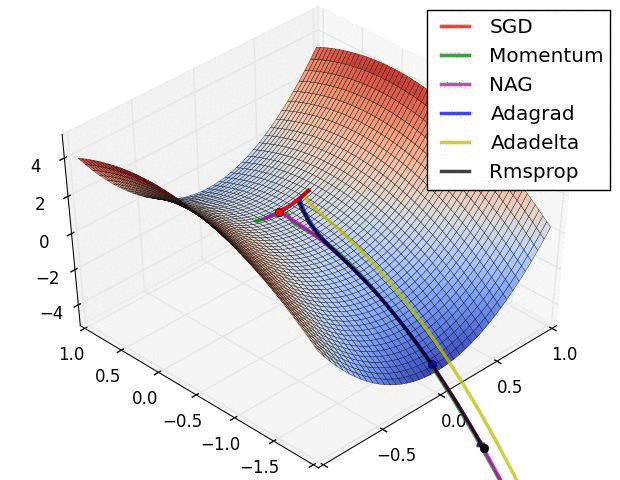
从上面的动画可以看出,自适应算法能很快收敛,并快速找到参数更新中正确的目标方向;而标准的SGD、NAG和动量项等方法收敛缓慢,且很难找到正确的方向。
背景知识:
深度学习优化算法入门:一、梯度下降
参考资料:
http://blog.csdn.net/red_stone1/article/details/78348753
http://imgtec.eetrend.com/blog/9908
http://www.datakit.cn/blog/2016/07/04/sgd_01.html