推荐系统总结

介绍

推荐系统是一种信息过滤系统，用于预测用户对物品的“评分”或“偏好”。

常用的算法如下：
1. 规则模型 （Apriori算法）
2. 协同过滤 ：仅仅基于用户行为数据设计的推荐算法一般称为协同过滤算法

协同过滤中的算法包括：1.基于邻域的方法 2.隐语义模型 3.基于图的随机游走算法
基于领域的方法应用最为广泛：包含基于用户的协同过滤以及基于物品的协同过滤算法

推荐系统评测指标

1. 用户满意度
2. 预测准确度
   2.1 评分预测: 评分预测的预测准确度一般通过均方根误差（RMSE）和平均绝对误差（MAE）计算
   2.2 TopN推荐：一般通过准确率（precision）/召回率（recall）度
   召回率：
   准确率：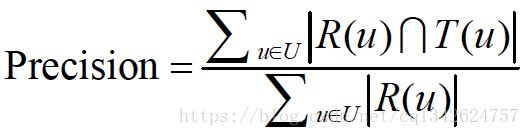
   其中：R(u)是根据用户在训练集上的行为给用户作出的推荐列表，而T(u)是用户在测试集上的行为列表
3. 覆盖率：覆盖率（coverage）描述一个推荐系统对物品长尾的发掘能力。覆盖率有不同的定义方法，最简单的定义为推荐系统能够推荐出来的物品占总物品集合的比例。但是上面的定义过于粗略。覆盖率为100%的系统可以有无数的物品流行度分布。为了更细
   致地描述推荐系统发掘长尾的能力，需要统计推荐列表中不同物品出现次数的分布。如果所有的物品都出现在推荐列表中，且出现的次数差不多，那么推荐系统发掘长尾的能力就很好。
   在信息论和经济学中有两个著名的指标可以用来定义覆盖率。第一个是信息熵，第二个指标是基尼系数（Gini Index）
4. 多样性：为了满足用户广泛的兴趣，推荐列表需要能够覆盖用户不同的兴趣领域，即推荐结果需要具有多样性。多样性描述了推荐列表中物品两两之间的不相似性。因此，多样性和相似性是对应的。假设 s(i,j) s ( i , j ) 定义了物品i和j之间的相似度，那么用户u的推荐列表R(u)的多样性定义如下：
   
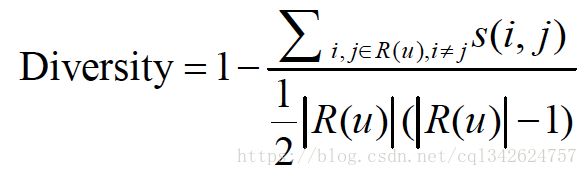
   而推荐系统的整体多样性可以定义为所有用户推荐列表多样性的平均值：
   
5. 新颖性: 新颖的推荐是指给用户推荐那些他们以前没有听说过的物品。评测新颖度的最简单方法是利用推荐结果的平均流行度，因为越不热门的物品越可能让用户觉得新颖
6. 惊喜度: 如果推荐结果和用户的历史兴趣不相似，但却让用户觉得满意，那么就可以说推荐结果的惊喜度很高，而推荐的新颖性仅仅取决于用户是否听说过这个推荐结果。目前并没有什么公认的惊喜度指标定义方式，这里只给出一种定性的度量方式。上面提到，令用户惊喜的推荐结果是和用户历史上喜欢的物品不相似，但用户却觉得满意的推荐。那么，定义惊喜度需要首先定义推荐结果和用户历史上喜欢的物品的相似度，其次需要定义用户对推荐结果的满意度。
7. 信任度：这两个人可以看做两个推荐系统，尽管他们的推荐结果相同，但用
   户却可能产生不同的反应，这就是因为用户对他们有不同的信任度。
8. 实时性：推荐系统的实时性包括两个方面。首先，推荐系统需要实时地更新推荐列表来满足用户新的行为变化。实时性的第二个方面是推荐系统需要能够将新加入系统的物品推荐给用户。这主要考验了推荐系统处理物品冷启动的能力。
9. 健壮性：健壮性（即robust,鲁棒性）指标衡量了一个推荐系统抗击作弊的能力。
10. 商业目标：很多时候，网站评测推荐系统更加注重网站的商业目标是否达成，而商业目标和网站的盈利模式是息息相关的。

规则模型（Apriori算法）

1. 找出所有频繁项集，频繁性大于等于最小支持度
2. 根据频繁项集产生强关联规则，并满足最小支持度和最小置信度

支持度 （X=>Y） = (包含X和Y的记录数)／（数据集记录总数）
置信度（X=>Y) = （包含X和Y的记录数）／（数据集包含X的记录数）

频繁定理：频繁项集的非空子集必须是频繁的。

协同过滤

基本步骤：
1. 收集用户偏好信息
2. 寻找相似商品或用户
3. 推荐

基于用户的协同过滤

步骤：
(1) 找到和目标用户兴趣相似的用户集合。
(2) 找到这个集合中的用户喜欢的，且目标用户没有听说过的物品推荐给目标用户。

用户间相似度计算
相似度函数s ：皮尔孫相关系数／余弦相似度

暴力方式：两两用户计算相似度
问题：复杂度O(|U|*|U|) ，很多用户之间没有对相同的物品产生过行为。

换一种思路：首先计算出|N(u) 交 N(v)| !=0 的用户对(u,v) ，再对这种情况除以分母
方法：建立物品到用户的倒排表，每个物品保存访问过的用户列表。
令C[u][v]=|N(u) 交 N(v)|。若u, v 同时 in K个物品的倒排表，C[u][v]=K。
可以扫描倒排表中每个物品对应的用户列表，将用户列表中的两两用户对应的C[u][v]加1，最终就可以得到所有用户之间不为0的C[u][v]。

推荐
得到用户之间的兴趣相似度后，UserCF算法会给用户推荐和他兴趣最相似的K个用户喜欢的
物品。如下的公式度量了UserCF算法中用户u对物品i的感兴趣程度.

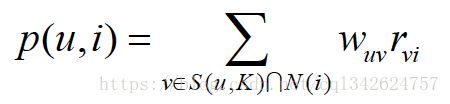
其中，S(u, K)包含和用户u兴趣最接近的K个用户，N(i)是对物品i有过行为的用户集合， wuv w u v 是用户u和用户v的兴趣相似度， rvi r v i 代表用户v对物品i的兴趣，因为使用的是单一行为的隐反馈数据，所以所有的 rvi r v i =1。

用户相似度计算的改进：
以图书为例，如果两个用户都曾经买过《新华字典》，这丝毫不能说明他们兴趣相似，
因为绝大多数中国人小时候都买过《新华字典》。但如果两个用户都买过《数据挖掘导论》，那可以认为他们的兴趣比较相似，因为只有研究数据挖掘的人才会买这本书。换句话说，两个用户对冷门物品采取过同样的行为更能说明他们兴趣的相似度

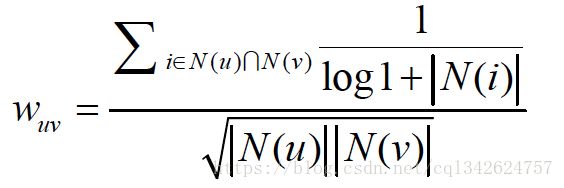
惩罚了用户u和用户v共同兴趣列表中热门物品对他们相似度的影响。

基于物品的协同过滤

基于用户的协同过滤算法在一些网站（如Digg）中得到了应用，但该算法有一些缺点。
首先，随着网站的用户数目越来越大，计算用户兴趣相似度矩阵将越来越困难，其运算时间复杂度和空间复杂度的增长和用户数的增长近似于平方关系。
其次，基于用户的协同过滤很难对推荐结果作出解释。
因此，著名的电子商务公司亚马逊提出了另一个算法——基于物品的协同过滤算法

该算法认为，物品A和物品B具有很大的相似度是因为喜欢物品A的用户大都也喜欢物品
B

基于物品的协同过滤算法主要分为两步。
(1) 计算物品之间的相似度。
(2) 根据物品的相似度和用户的历史行为给用户生成推荐列表。

Item 之间的相似度

分母|N(i)|是喜欢物品i的用户数，而分子 N(i) N( j) 是同时喜欢物品i和物品j的用户
数，这个公式惩罚了物品j的权重，因此减轻了热门物品会和很多物品相似的可能性

和UserCF算法类似，用ItemCF算法计算物品相似度时也可以首先建立用户—物品倒排表（即对每个用户建立一个包含他喜欢的物品的列表），然后对于每个用户，将他物品列表中的物品两两在共现矩阵C中加1。详细代码如下所示：

在得到物品之间的相似度后，ItemCF通过如下公式计算用户u对一个物品j的兴趣：

这里N(u)是用户喜欢的物品的集合，S(j,K)是和物品j最相似的K个物品的集合， wji w j i 是物品j和i的相似度，rui是用户u对物品i的兴趣。该公式的含义是，和用户历史上感兴趣的物品越相似的物品，越有可能在用户的推荐列表中获得比较高的排名。

UserCF和ItemCF的综合比较

UserCF给用户推荐那些和他有共同兴趣爱好的用户喜欢的物品，而ItemCF给用户推荐那些和他之前喜欢的物品类似的物品。从这个算法的原理可以看到，UserCF的推荐结果着重于反映和用户兴趣相似的小群体的热点，而ItemCF的推荐结果着重于维系用户的历史兴趣。

换句话说，UserCF的推荐更社会化，反映了用户所在的小型兴趣群体中物品的热门程度，而ItemCF的推荐更加个性化，反映了用户自己的兴趣传承。

隐语义模型（待更新）

基于图的模型（待更新）

基于贝叶斯的推荐方法

基于KNN的推荐方法

决策树算法

基于矩阵分解的推荐方法

用户-商品矩阵(评分矩阵)，记为 Rm×n R m × n 。可以将其分解成两个或者多个矩阵的乘积，假设分解成两个矩阵 Pm×k P m × k 和 Qk×n Q k × n ，我们要使得矩阵 Pm×k P m × k 和 Qk×n Q k × n 的乘积能够还原原始的矩阵 Rm×n R m × n ：
其中，矩阵 Pm×k P m × k 表示的是m个用户与k个主题之间的关系，而矩阵 Qk×n Q k × n 表示的是k个主题与n个商品之间的关系。

求解：用原始的评分矩阵 Rm×n R m × n 与重新构建的评分矩阵 R̂ ′m×n R ̂ m × n ′ 之间的误差的平方作为损失函数, 梯度下降

预测：利用上述的过程，我们可以得到矩阵 Pm×k P m × k 和 Qk×n Q k × n ，这样便可以为用户i对商品j进行打分：

基于BP的推荐方法

基于W2V的推荐方法

word2vec 在没有词性标注的情况下，能够从原始语料学习到单词的向量表示，比较单词间的语义、句法的相似性。

我们可以把商品看作单词，把每个用户喜欢的商品序列看作句子，用这些数据训练 word2vec 模型，得到每个商品的向量表示。在推荐时，根据用户已经买或者浏览的商品 ，在向量空间中找到与其距离相近的商品作为推荐。

优点：向量可以相加、相减，能够更灵活地满足个性化推荐需求

基于LR的推荐方法

基于深度学习的推荐方法

FM 模型

对于因子分解机FM来说，最大的特点是对于稀疏的数据具有很好的学习能力。现实中稀疏的数据很多：

FNN 模型

PNN 模型

wide&deep 模型

deepFM模型

Wide & Deep Learning通过组合使用cross-product transformation特征的线性模型和DNN模型进行Joint train从而实现memorization和generalization的结合。但是对于Wide模型来说还是需要做一些特征交叉来实现memorization，而因子分解机(Factorization Machines, FM)通过对于每一维特征的隐变量内积来提取特征组合，最终的结果也非常好。虽然理论上来讲FM可以对高阶特征组合进行建模，但实际上因为计算复杂度的原因一般都只用到了二阶特征组合。

对于离散特征的处理，我们使用的是将特征转换成为one-hot的形式，但是将One-hot类型的特征输入到DNN中，会导致网络参数太多难以训练，此时可以借鉴word2vec的思路，进行embedding。将Onehot编码后的向量经过一个embedding层输出Dense Vector。
具体的思路就是，将一个特征Onehot编码后会生成多个特征，但是每个特征里面只有一个为1，其他都为0，这些由一个特征生成的多个互斥的特征引用FFM的思想的话就属于一个Field。

如果将embedding层的输出再加两层的全连接层，让Dense Vector进行组合，那么高阶特征的组合就出来了。

但是低阶和高阶特征组合隐含地体现在隐藏层中，如果我们希望把低阶特征组合单独建模，然后融合高阶特征组合。也就是我们需要学习低阶的特征组合，也需要学习高阶的特征组合。即将DNN与FM进行一个合理的融合：

DeepFm模型：

DeepFM包含两部分：神经网络部分与因子分解机部分，分别负责低阶特征的提取和高阶特征的提取。这两部分共享同样的输入。DeepFM的预测结果可以写为：

FM部分是一个因子分解机:关于因子分解机可以参阅文章[Rendle, 2010] Steffen Rendle. Factorization machines. In ICDM, 2010.。因为引入了隐变量的原因，对于几乎不出现或者很少出现的隐变量，FM也可以很好的学习.

深度部分是一个前馈神经网络。与图像或者语音这类输入不同，图像语音的输入一般是连续而且密集的，然而用于CTR的输入一般是及其稀疏的。因此需要重新设计网络结构。具体实现中为，在第一层隐含层之前，引入一个嵌入层来完成将输入向量压缩到低维稠密向量。

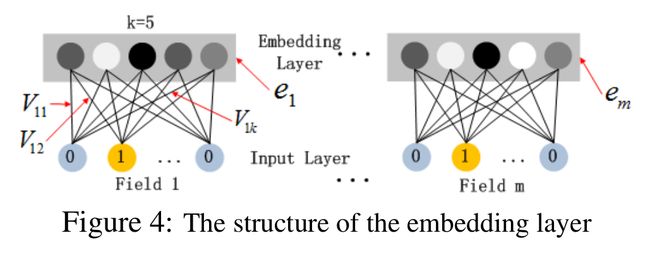
对于Fig.4这个网络结构有两个很有意思的point：

1）虽然输入的field vector长度不一，但是它们embedding出来的长度是固定的；

2）FM的latent vector V向量作为原始特征到embedding vector的权重矩阵，放在网络里学习

NFM模型

AFM模型

DSSM模型

MV-DNN模型

DCN模型

NCF模型

GBDT+LR模型

图中共有两棵树，x为一条输入样本，遍历两棵树后，x样本分别落到两颗树的叶子节点上，每个叶子节点对应LR一维特征，那么通过遍历树，就得到了该样本对应的所有LR特征。构造的新特征向量是取值0/1的。举例来说：上图有两棵树，左树有三个叶子节点，右树有两个叶子节点，最终的特征即为五维的向量。对于输入x，假设他落在左树第一个节点，编码[1,0,0]，落在右树第二个节点则编码[0,1]，所以整体的编码为[1,0,0,0,1]，这类编码作为特征，输入到LR中进行分类。

缺点：
现在的业务数据是什么？是大量离散特征导致的高维度离散数据。而树模型对这样的离散特征，是不能很好处理的，要说为什么，因为这容易导致过拟合。

seq2seq模型

参考：《推荐系统实践》项亮
http://davidlau.me/2017/03/06/word2vec-collaborative-filtering/
https://blog.csdn.net/iyuanshuo/article/details/80155086
https://blog.csdn.net/google19890102/article/details/45532745