信号系统笔记(二)连续系统的时域分析
信号系统笔记(二)连续系统的时域分析
- 2 连续系统的时域分析
- 2.1 连续系统的响应
- 2.1.1 连续系统建立微分方程
- 2.1.2 微分方程的模拟框图
- 2.1.3 微分方程的经典解法
- 2.1.4 连续系统的初始值
- 2.1.5 零输入响应
- 2.1.6 零状态响应
- 2.1.7 响应分类
- 2.2 冲激响应与阶跃响应
- 2.2.1 冲激响应及其求法
- 2.2.2 阶跃响应及其求法
- 2.3 卷积积分
- 2.3.1 信号的时域分解
- 2.3.2 卷积公式
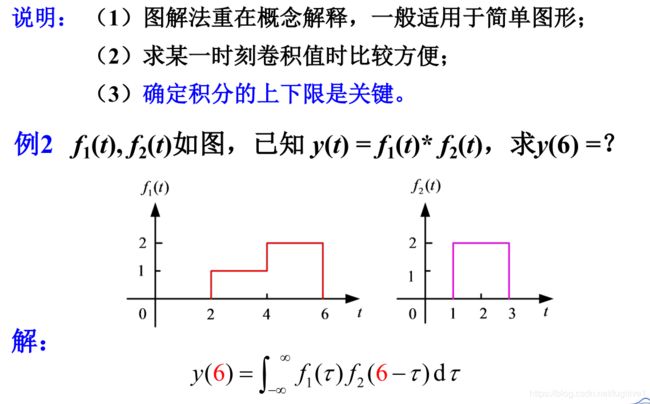
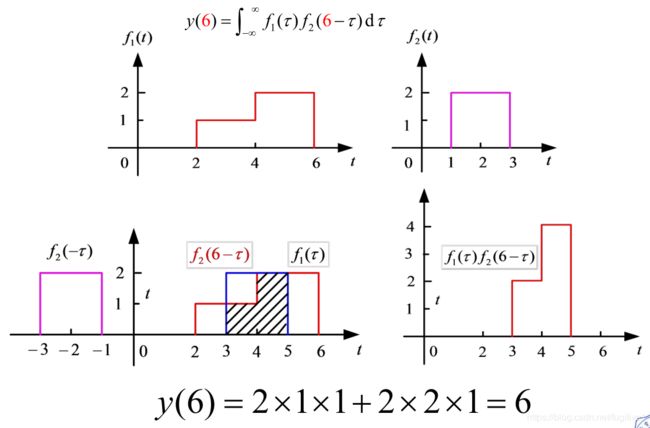
- 2.3.3 卷积积分的图解法
- 2.3.4 卷积积分的代数性质
- 2.3.5 卷积积分的微积分性质
- 2.3.6 卷积积分的时移性质
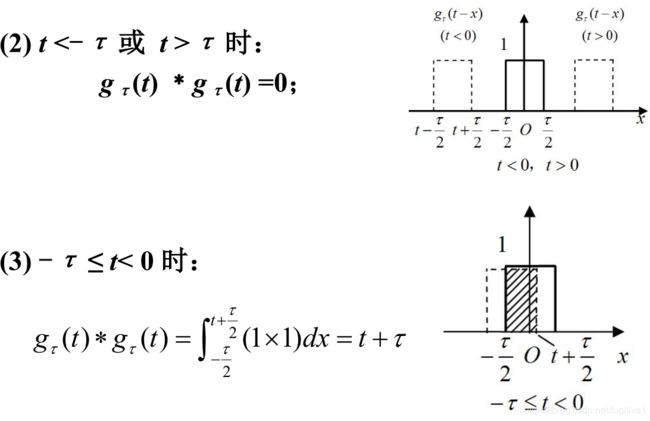
- 2.3.7 常用的卷积积分公式
- 2.3.8 用梳状函数卷积产生周期信号
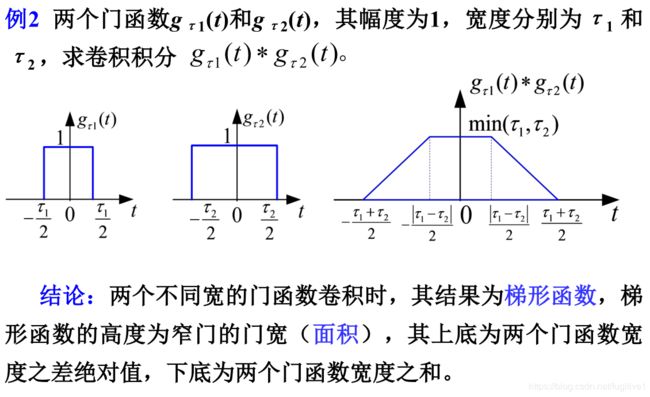
- 2.3.9 矩形脉冲的卷积产生三角形和梯形脉冲
- 2.4 相关函数
- 2.4.1 互相关和自相关函数的定义
- 2.4.2 卷积与相关的比较
- 2.5 连续系统的微分算子描述
- 2.5.1 微分算子P的定义
- 2.5.2 微分算子P的性质
- 2.5.3 传输算子 H ( P ) H(P) H(P)
- 2.6 总结
2 连续系统的时域分析
从这一章开始,知识变得难起来了,学着有点让人头秃,不过慢慢来,一步一个脚印。
2.1 连续系统的响应
2.1.1 连续系统建立微分方程
根据之前提到的知识,系统,本质是可以理解成一个“函数”,给定一个输入,然后得到输出。函数体一般为微分方程,如电路图:
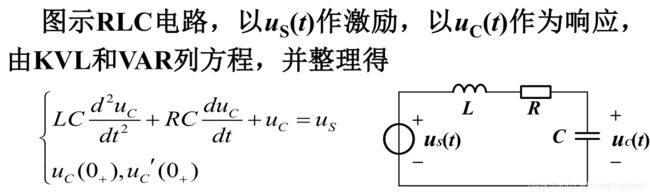
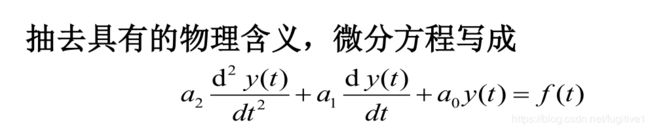
该方程为二阶线性微分方程,当然,不只是,电路图,其他系统也可以用微分方程来描述:

2.1.2 微分方程的模拟框图
我目前觉得,引入微分方程的模拟框图,是为了更加明确输入跟输出。二阶线性微分方程的一般形式如下:
y ′ ′ ( t ) + a 1 y ′ ( t ) + a 0 y ( t ) = f ( t ) y''(t)+a_1y'(t)+a_0y(t)=f(t) y′′(t)+a1y′(t)+a0y(t)=f(t)
其中 f ( t ) f(t) f(t)为系统的输入, y ( t ) y(t) y(t)为系统的输出。方程左边为系统的模型(类比于函数体),右边为输入函数(类比于函数输入值)。
可以由三种基本运算来描述一个系:相加、积分、数乘,分别对应框图中的,加法器、积分器、数乘器。


以下是实例解释微分方程框图的画法,如系统: y ′ ′ ( t ) + a y ′ ( t ) + b y ( t ) = f ( t ) y''(t)+ay'(t)+by(t)=f(t) y′′(t)+ay′(t)+by(t)=f(t),化为框图的步骤:
- 将方程变形为: y ′ ′ ( t ) = f ( t ) − a y ′ ( t ) − b y ( t ) y''(t)=f(t)-ay'(t)-by(t) y′′(t)=f(t)−ay′(t)−by(t)
- 画出两个积分器:
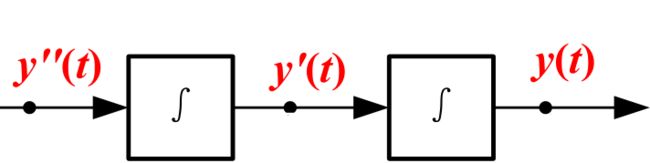
- 然后按照第一步的方程拼接
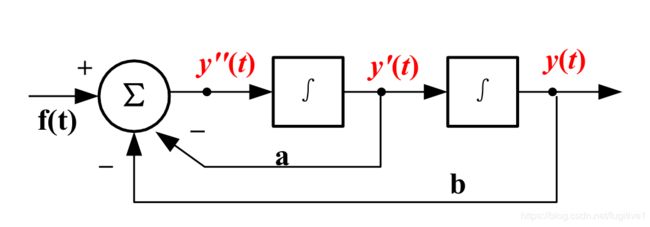
当输入中也含有微分的情况下,如系统: y ′ ′ ( t ) + 3 y ′ ( t ) + 2 y ( t ) = 4 f ′ ( t ) + f ( t ) y''(t)+3y'(t)+2y(t)=4f'(t)+f(t) y′′(t)+3y′(t)+2y(t)=4f′(t)+f(t),画框图需要引进辅助函数: x ′ ′ ( t ) + 3 x ′ ( t ) + 2 x ( t ) = f ( t ) x''(t)+3x'(t)+2x(t)=f(t) x′′(t)+3x′(t)+2x(t)=f(t),这个函数的系统跟上面那个系统一样,只不过输入为 f ( t ) f(t) f(t),输出为 x ( t ) x(t) x(t)。
由于是LTI系统,因此系统具线性,即: f ( t ) → x ( t ) f(t) \to x(t) f(t)→x(t), f ′ ( t ) → x ′ ( t ) f'(t) \to x'(t) f′(t)→x′(t), f ( t ) + 4 f ′ ( t ) → x ( t ) + x f ′ ( t ) = y ( t ) f(t)+4f'(t) \to x(t)+xf'(t)=y(t) f(t)+4f′(t)→x(t)+xf′(t)=y(t)
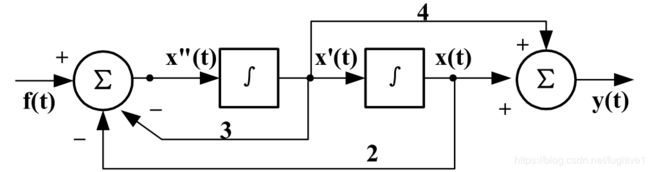
当然,框图跟方程可以互相转换,如下框图:

可以转换为方程: y ′ ′ ( t ) + 2 y ′ ( t ) + 3 y ( t ) = 3 f ( t ) + 4 f ′ ( t ) y''(t)+2y'(t)+3y(t)=3f(t)+4f'(t) y′′(t)+2y′(t)+3y(t)=3f(t)+4f′(t)
2.1.3 微分方程的经典解法
关于微分方程的经典解法,在学高等数学的时候就很懵逼,不知其原理只知其解法步骤,因为只知道解法步骤就足够了。一般来说,解法如下图所示:

其中,二阶线性微分方程的解法如下:
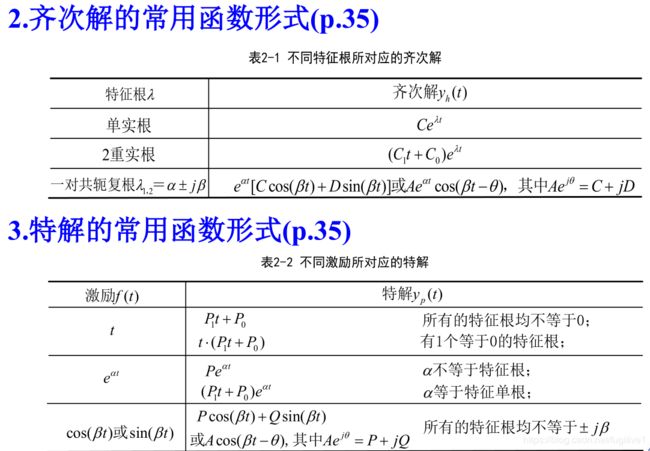
2.1.4 连续系统的初始值
初始值是 n n n阶系统在 t = 0 t=0 t=0时接入系统的时候,其响应在 t = 0 + t=0_+ t=0+时刻的值,即 y ( j ) ( 0 + ) ( j = 0 , 1 , . . . , n − 1 ) y^{(j)}(0_+)(j=0,1,...,n-1) y(j)(0+)(j=0,1,...,n−1)。
初始状态是指系统在激励未接入的 t = 0 − t=0_- t=0−时刻的响应值 y ( j ) ( 0 − ) y^{(j)}(0_-) y(j)(0−),这个值反映了系统的历史情况,与激励无关系。
一般来说,需要从初始状态求得初始值,即: y ( j ) ( 0 − ) → y ( j ) ( 0 + ) y^{(j)}(0_-) \to y^{(j)}(0_+) y(j)(0−)→y(j)(0+)。
例如:

带入输入信号得到: y ′ ′ ( t ) + 3 y ′ ( t ) + 2 y ( t ) = 2 δ ( t ) + 6 ε ( t ) y''(t)+3y'(t)+2y(t)=2\delta(t)+6\varepsilon(t) y′′(t)+3y′(t)+2y(t)=2δ(t)+6ε(t),观察此方程,右边含有 δ ( t ) \delta(t) δ(t),说明 y ′ ′ ( t ) y''(t) y′′(t)中含有 δ ( t ) \delta(t) δ(t),因为如果 y ′ ( t ) y'(t) y′(t)含有 δ ( t ) \delta(t) δ(t)的话,那么 y ′ ′ ( t ) y''(t) y′′(t)中必含有 δ ′ ( t ) \delta'(t) δ′(t),但是等式右边不含有 δ ′ ( t ) \delta'(t) δ′(t)。
PS:这里可能会考虑到为什么等式右边没有对应到 y ( t ) y(t) y(t), y ′ ′ ( t ) y''(t) y′′(t)必含有 δ ( t ) \delta(t) δ(t),则: y ′ ( t ) y'(t) y′(t)必含有 ε ( t ) \varepsilon(t) ε(t),那么 y ( t ) y(t) y(t)必含有 ε ( t ) \varepsilon(t) ε(t)的积分,这个在等式右边没有体现,我没想清楚为什么。
按照上面的思路, y ′ ′ ( t ) y''(t) y′′(t)中含有 δ ( t ) \delta(t) δ(t), y ′ ( t ) y'(t) y′(t)含有 ε ( t ) \varepsilon(t) ε(t),因此有: y ′ ( 0 − ) ≠ y ′ ( 0 + ) y'(0_-) \neq y'(0_+) y′(0−)=y′(0+), y ( 0 − ) = y ( 0 + ) = 2 y(0_-)=y(0_+)=2 y(0−)=y(0+)=2。对等式两边同时求 0 − → 0 + 0_-\to0_+ 0−→0+的积分得到:
∫ 0 − 0 + y ′ ′ ( t ) d t + 3 ∫ 0 − 0 + y ′ ( t ) d t + 2 ∫ 0 − 0 + y ( t ) d t = 2 ∫ 0 − 0 + δ ( t ) d t + 6 ∫ 0 − 0 + ε ( t ) d t \int_{0_-}^{0_+}y''(t){\rm d}t+3\int_{0_-}^{0_+}y'(t){\rm d}t+2\int_{0_-}^{0_+}y(t){\rm d}t=2\int_{0_-}^{0_+}\delta(t){\rm d}t+6\int_{0_-}^{0_+}\varepsilon(t){\rm d}t ∫0−0+y′′(t)dt+3∫0−0+y′(t)dt+2∫0−0+y(t)dt=2∫0−0+δ(t)dt+6∫0−0+ε(t)dt
y ′ ( 0 + ) − y ′ ( 0 − ) = 2 y'(0_+)-y'(0_-)=2 y′(0+)−y′(0−)=2
因此得到: y ( 0 + ) = 2 , y ′ ( 0 + ) = 2 y(0_+)=2,y'(0_+)=2 y(0+)=2,y′(0+)=2
结论:微分方程等号右端含有 δ ( t ) \delta(t) δ(t) 时 , 仅在等号左端 y ( t ) y(t) y(t)的最高阶导数中含有 δ ( t ) \delta(t) δ(t) , 则 y ( t ) y(t) y(t) 的次高阶跃变 , 其余连续;若右端不含冲激函数 , 则不会跃变。
2.1.5 零输入响应

例题:

该系统为零输入响应,则有: y ′ ′ ( t ) + 3 y ′ ( t ) + 2 y ( t ) = 0 y''(t)+3y'(t)+2y(t)=0 y′′(t)+3y′(t)+2y(t)=0
y ( 0 − ) = y ( 0 + ) = 2 , y ′ ( 0 − ) = y ′ ( 0 + ) = 0 y(0_-)=y(0_+)=2,y'(0_-)=y'(0_+)=0 y(0−)=y(0+)=2,y′(0−)=y′(0+)=0
该方程是个齐次微分方程,特征方程为 r 2 + 3 r + 2 = 0 r^2+3r+2=0 r2+3r+2=0, r 1 = − 1 , r 2 = − 2 r_1=-1,r_2=-2 r1=−1,r2=−2。因此设定通解为: y ( t ) = C 1 e − t + C 2 e − 2 t y(t)=C_1e^{-t}+C_2e^{-2t} y(t)=C1e−t+C2e−2t,带入值解得零输入响应为:
y ( t ) = 4 e − t − 2 e − 2 t y(t)=4e^{-t}-2e^{-2t} y(t)=4e−t−2e−2t
2.1.6 零状态响应

例题:

零输入响应跟上面一样,零状态响应求法如下,根据零状态响应的特质,可以得到: y z s ( 0 − ) = 0 , y z s ′ ( 0 − ) = 0 y_{zs}(0_-)=0,y'_{zs}(0_-)=0 yzs(0−)=0,yzs′(0−)=0,现在要求 y z s ( 0 + ) , y z s ′ ( 0 + ) y_{zs}(0_+),y'_{zs}(0_+) yzs(0+),yzs′(0+)。原微分方程化为:
y ′ ′ ( t ) + 3 y ′ ( t ) + 2 y ( t ) = 2 δ ( t ) + 6 ε ( t ) y''(t)+3y'(t)+2y(t)=2\delta(t)+6\varepsilon(t) y′′(t)+3y′(t)+2y(t)=2δ(t)+6ε(t)
由匹配法知(见2.1.4节): y z s ( 0 − ) = y z s ( 0 + ) = 0 , y z s ′ ( 0 + ) = 2 y_{zs}(0_-)=y_{zs}(0_+)=0,y'_{zs}(0_+)=2 yzs(0−)=yzs(0+)=0,yzs′(0+)=2
当 t > 0 t>0 t>0时, y ′ ′ ( t ) + 3 y ′ ( t ) + 2 y ( t ) = 6 y''(t)+3y'(t)+2y(t)=6 y′′(t)+3y′(t)+2y(t)=6
齐次方程的通解为: y z s h ( t ) = C 1 e − t + C 2 e − 2 t y_{zsh}(t)=C_1e^{-t}+C_2e^{-2t} yzsh(t)=C1e−t+C2e−2t解得: y z s h ( t ) = − 4 e − t + e − 2 t y_{zsh}(t)=-4e^{-t}+e^{-2t} yzsh(t)=−4e−t+e−2t
设定特解为: y z s p ( t ) = p y_{zsp}(t)=p yzsp(t)=p,带入方程解得 p = 3 p=3 p=3解得零状态响应为:
y z s ( t ) = − 4 e − t + e − 2 t + 3 y_{zs}(t)=-4e^{-t}+e^{-2t}+3 yzs(t)=−4e−t+e−2t+3
2.1.7 响应分类
2.2 冲激响应与阶跃响应
2.2.1 冲激响应及其求法
冲激响应是由单位冲激函数 δ ( t ) \delta(t) δ(t)所引起的零状态响应,记为 h ( t ) h(t) h(t)。
h ( t ) h(t) h(t)隐含的条件:
f ( t ) = δ ( t ) f(t)=\delta(t) f(t)=δ(t)
h ( 0 − ) = h ′ ( 0 − ) = 0 h(0_-)=h'(0_-)=0 h(0−)=h′(0−)=0
其中第二个条件是所有二阶零状态响应都成立。

例题如下:
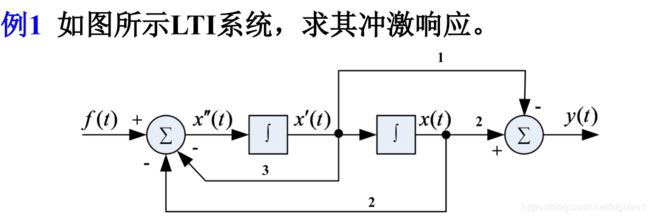
先求其系统的方程:
x ′ ′ ( t ) = f ( t ) − 2 x ( t ) − 3 x ′ ( t ) → x ′ ′ ( t ) + 3 x ′ ( t ) + 2 x ( t ) = f ( t ) x''(t)=f(t)-2x(t)-3x'(t) \to x''(t)+3x'(t)+2x(t)=f(t) x′′(t)=f(t)−2x(t)−3x′(t)→x′′(t)+3x′(t)+2x(t)=f(t),系统方程为:
y ′ ′ ( t ) + 3 y ′ ( t ) + 2 y ( t ) = − f ′ ( t ) + 2 f ( t ) y''(t)+3y'(t)+2y(t)=-f'(t)+2f(t) y′′(t)+3y′(t)+2y(t)=−f′(t)+2f(t),
设 h 1 ′ ′ ( t ) + 3 h 1 ′ ( t ) + 2 h 1 ( t ) = δ ( t ) h_1''(t)+3h_1'(t)+2h_1(t)=\delta(t) h1′′(t)+3h1′(t)+2h1(t)=δ(t),由于二阶线性零状态响应初始条件有:
h ( 0 − ) = h ′ ( 0 − ) = 0 h(0_-)=h'(0_-)=0 h(0−)=h′(0−)=0。
由系数匹配法得到: h ′ ( 0 − ) ≠ h ′ ( 0 + ) , h ( 0 − ) = h ( 0 + ) = 0 h'(0_-)\neq h'(0_+),h(0_-)=h(0_+)=0 h′(0−)=h′(0+),h(0−)=h(0+)=0
两端从 0 − → 0 + 0_- \to 0_+ 0−→0+积分得到:
∫ 0 − 0 + h 1 ′ ′ ( t ) + 3 ∫ 0 − 0 + h 1 ′ ( t ) + 2 ∫ 0 − 0 + h 1 ( t ) = ∫ 0 − 0 + δ ( t ) \int_{0_-}^{0_+}h_1''(t)+3\int_{0_-}^{0_+}h_1'(t)+2\int_{0_-}^{0_+}h_1(t)=\int_{0_-}^{0_+}\delta(t) ∫0−0+h1′′(t)+3∫0−0+h1′(t)+2∫0−0+h1(t)=∫0−0+δ(t)
h 1 ′ ( 0 + ) − h 1 ′ ( 0 − ) = 1 h'_1(0_+)-h'_1(0_-)=1 h1′(0+)−h1′(0−)=1
因此得到初始值: h ( 0 + ) = 0 , h ′ ( 0 + ) = 1 h(0_+)=0,h'(0_+)=1 h(0+)=0,h′(0+)=1
当 t > 0 t>0 t>0时 ,方程化为: h 1 ′ ′ ( t ) + 3 h 1 ′ ( t ) + 2 h 1 ( t ) = 0 h_1''(t)+3h_1'(t)+2h_1(t)=0 h1′′(t)+3h1′(t)+2h1(t)=0,其特征跟分别为 r 1 = − 1 , r 2 = − 2 r_1=-1,r_2=-2 r1=−1,r2=−2,因此设定解为 h 1 ( t ) = C 1 e − 1 t + C 2 e − 2 t h_1(t)=C_1e^{-1t}+C_2e^{-2t} h1(t)=C1e−1t+C2e−2t,带入初始值得到: h 1 ( t ) = ( e − 1 t − 2 e − 2 t ) ε ( t ) h_1(t)=(e^{-1t}-2e^{-2t})\varepsilon(t) h1(t)=(e−1t−2e−2t)ε(t)
因此 − f ′ ( t ) + 2 f ( t ) → − h 1 ′ ( t ) + 2 h 1 ( t ) = ( 3 e − 1 t − 4 e − 2 t ) ε ( t ) -f'(t)+2f(t)\to -h_1'(t)+2h_1(t)=(3e^{-1t}-4e^{-2t})\varepsilon(t) −f′(t)+2f(t)→−h1′(t)+2h1(t)=(3e−1t−4e−2t)ε(t)
2.2.2 阶跃响应及其求法
2.3 卷积积分
2.3.1 信号的时域分解
p ( t ) p(t) p(t)的面积为 1 1 1,宽度为 Δ \Delta Δ,因此高度为 1 Δ \frac{1}{\Delta} Δ1。当 Δ → 0 \Delta \to 0 Δ→0, p ( t ) → δ ( t ) p(t) \to \delta(t) p(t)→δ(t)。


2.3.2 卷积公式
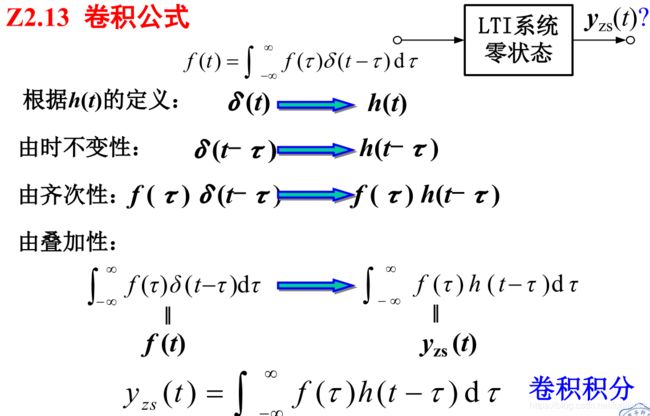

![]()
解: f ( t ) = f 1 ( t ) ∗ f 2 ( t ) = ∫ − ∞ ∞ f 1 ( τ ) f 2 ( t − τ ) d τ = ∫ − ∞ ∞ e − t ε ( τ ) ε ( t − τ ) d τ f(t)=f_1(t)*f_2(t)=\int_{-\infty}^{\infty}f_1(\tau)f_2(t-\tau) {\rm d}\tau=\int_{-\infty}^{\infty}e^{-t}\varepsilon(\tau)\varepsilon(t-\tau) {\rm d}\tau f(t)=f1(t)∗f2(t)=∫−∞∞f1(τ)f2(t−τ)dτ=∫−∞∞e−tε(τ)ε(t−τ)dτ
由于单位阶跃函数在小于零时为零,因此该积分只在 τ > 0 \tau >0 τ>0且 τ < t \tau < t τ<t有取值(这里有个隐含的含义,就是 t > 0 t>0 t>0),且在这个范围内 ε \varepsilon ε的值取 1 1 1,积分限变为 0 → t 0 \to t 0→t:
∫ 0 t e − t ε ( τ ) ε ( t − τ ) d τ = ∫ 0 t e − t d τ ε ( t ) = [ − e − τ ] 0 t ε ( t ) = ( 1 − e − t ) ε ( t ) \int_0^te^{-t}\varepsilon(\tau)\varepsilon(t-\tau) {\rm d}\tau=\int_0^te^{-t} {\rm d}\tau\varepsilon(t)=[-e^{-\tau}]_{0}^{t}\varepsilon(t)=(1-e^{-t})\varepsilon(t) ∫0te−tε(τ)ε(t−τ)dτ=∫0te−tdτε(t)=[−e−τ]0tε(t)=(1−e−t)ε(t)
2.3.3 卷积积分的图解法
2.3.4 卷积积分的代数性质
2.3.5 卷积积分的微积分性质
2.3.6 卷积积分的时移性质

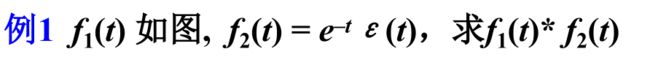

函数 f 1 ( t ) f_1(t) f1(t)可以表示为两个阶跃函数的差: f 1 ( t ) = ε ( t ) − ε ( t − 2 ) f_1(t)=\varepsilon(t)-\varepsilon(t-2) f1(t)=ε(t)−ε(t−2)
f 1 ( t ) ∗ f 2 ( t ) = ( ε ( t − 2 ) − ε ( t ) ) ∗ f 2 ( t ) f_1(t)*f_2(t)=(\varepsilon(t-2)-\varepsilon(t))*f_2(t) f1(t)∗f2(t)=(ε(t−2)−ε(t))∗f2(t)
根据分配率得到:
ε ( t ) ∗ f 2 ( t ) − ε ( t ) ∗ f 2 ( t − 2 ) \varepsilon(t)*f_2(t)-\varepsilon(t)*f_2(t-2) ε(t)∗f2(t)−ε(t)∗f2(t−2)
其中:
ε ( t ) ∗ f 2 ( t ) = f 2 − 1 ( t ) = ( 1 − e − t ) ε ( t ) \varepsilon(t)*f_2(t)=f_2^{-1}(t)=(1-e^{-t})\varepsilon(t) ε(t)∗f2(t)=f2−1(t)=(1−e−t)ε(t)
f 2 − 1 ( t ) f_2^{-1}(t) f2−1(t)为 f 2 ( t ) f_2(t) f2(t)的积分,这里我有点不明白,感觉积分应该为 ( C − e − t ) (C-e^{-t}) (C−e−t),C为任意常数,而不是 ( 1 − e − t ) (1-e^{-t}) (1−e−t),说明一定有初始条件 f 2 − 1 ( 0 ) = 0 f_2^{-1}(0)=0 f2−1(0)=0才能使得 C = 1 C=1 C=1,我认为这里可以这样思考,积分代表函数图像与坐标轴围成的面积,当 t < 0 t<0 t<0的时候函数取值为0,因此当 t = 0 t=0 t=0时,函数与坐标轴围成的面积也为 0 0 0。
由卷积的时移特性得到:
ε ( t − 2 ) ∗ f 2 ( t ) = ( 1 − e − ( t − 2 ) ) ε ( t − 2 ) \varepsilon(t-2)*f_2(t)=(1-e^{-(t-2)})\varepsilon(t-2) ε(t−2)∗f2(t)=(1−e−(t−2))ε(t−2)
最终得到:
f 1 ( t ) ∗ f 2 ( t ) = ( 1 − e − t ) ε ( t ) − ( 1 − e − ( t − 2 ) ) ε ( t − 2 ) f_1(t)*f_2(t)=(1-e^{-t})\varepsilon(t)-(1-e^{-(t-2)})\varepsilon(t-2) f1(t)∗f2(t)=(1−e−t)ε(t)−(1−e−(t−2))ε(t−2)
2.3.7 常用的卷积积分公式
2.3.8 用梳状函数卷积产生周期信号

这个产生周期信号,在后面的数字信号处理会涉及到,公式 f ( t ) ∗ δ ( t − t 0 ) = f ( t − t 0 ) f(t)*\delta(t-t_0)=f(t-t_0) f(t)∗δ(t−t0)=f(t−t0),相当于把 f ( t ) f(t) f(t)向左平移了 t 0 t_0 t0个单位。 δ T ( t ) \delta_T(t) δT(t)是无数个周期为 T T T的 δ \delta δ,因此跟 δ T ( t ) \delta_T(t) δT(t)卷积自然就变成了周期函数。

2.3.9 矩形脉冲的卷积产生三角形和梯形脉冲
2.4 相关函数
2.4.1 互相关和自相关函数的定义


下面是相关函数的应用

用这个例子来理解相关函数中这个“相关”的含义,雷达发射的信号如上面的transmitted pulses f 1 ( t ) f_1(t) f1(t),接收的信号为received pulses f 2 ( t ) f_2(t) f2(t),相关函数为 ∫ − ∞ ∞ f 1 ( t ) ∗ f 2 ( t − τ ) \int_{-\infty}^{\infty}f_1(t)*f_2(t-\tau) ∫−∞∞f1(t)∗f2(t−τ)得到的是一个关于 τ \tau τ的函数,相关函数最大的时候得到的 τ \tau τ值就为雷达信号从发出到收到的时间间隔。
2.4.2 卷积与相关的比较
2.5 连续系统的微分算子描述
2.5.1 微分算子P的定义
2.5.2 微分算子P的性质
2.5.3 传输算子 H ( P ) H(P) H(P)
2.6 总结
这一章主要讲了连续时不变系统(LTI)的系统微分方程表示和解法,以及基本信号(冲激信号、阶跃信号)的响应。之后讲了信号在时域上的分解(卷积),引出了卷积积分以及相关函数,最后定义了微分算子 P P P以及传输算子 H ( P ) H(P) H(P)来更简便的描述系统的方程。