K 近邻法及其在手写数字识别的实践

文章首发于 个人博客

引言

k 近邻法（k-nearest-neighbor, KNN）是一种基本的分类和回归方法。现在只讨论其分类方面的应用，它不具备明显的学习过程，实际上是利用已知的训练数据集对输入特征向量空间进行划分，并作为其分类的“模型”。

其中 k 值的选择、距离的度量及分类决策规则是 k 近邻模型的三个基本要素。

本文将按照以下提纲进行：

• k 近邻法阐述
• k 近邻的模型
• k 近邻在手写数字识别上的实战

k 近邻法阐述

k 近邻算法非常容易理解，因为其本质上就是求距离，这是非常简单而直观的度量方法：对于给定的一个训练数据集，对新的输入实例 M，在训练数据集中找到与该新实例 M 最邻近的 k 个实例，由这 k 个实例按照一定的表决规则进行投票决策最合适的类别，那么实例 M 就属于这个类。下面是算法的描述：

k 近邻模型

k 近邻算法本质上是在超空间内划分区域空间分类的问题，在输入数据集的特征空间内，对于每个训练实例点 $x_i$ ，距离改点比其他点更近的所有点组成一个区域，叫做单元(cell)。上文说了 k 近邻模型的三个要素，k 值选择、距离度量、决策函数，下面一一说明。

k 值选择

k 值指的是选择近邻点的数目，如果 k = 1 则是最近邻，即是每次由距离新实例最近的训练点所属的类别决定待分类实例的类别。

k 值的选择对于 k 近邻法的结果可以产生重大影响。

当 k 值较小的时候，那么预测学习的近似误差会减少，因为此时只有距离待分类点较近的训练实例才会对于分类预测结果有影响作用，但是缺点是估计误差会增大，因为预测结果会对近邻的实例点非常敏感，如果近邻的实例多数都是噪声点，那么就很容易导致预测出错。即是说，k 值的减少意味着模型变得复杂，容易发生过拟合。

当 k 值较大的时候，就相当于用较大邻域中的训练实例进行预测。其优点是可以减少学习的估计误差。但缺点是学习的近似误差会增大，这时与输入实例较远的（不相似的）训练实例也会对预测起作用，使预测发生错误。k 值的增大就意味着整体的模型变得简单。

如果 k = N，那么无论输入实例是什么，都将简单地预测它属于在训练实例中最多的类。这时，模型过于简单，完全忽略训练实例中的大量有用信息，是不可取的。

在应用中，k 值一般取一个比较小的数值。通常采用交叉验证法来选取最优的 k 值。

距离度量

在实数域中，数的大小和两个数之间的距离是通过绝对值来度量的。在解析几何中，向量的大小和两个向量之差的大小是“长度”和“距离”的概念来度量的。为了对矩阵运算进行数值分析，我们需要对向量 和矩阵的“大小”引进某种度量。而范数是绝对值概念的自然推广。

特征空间中两个实例点的距离是其相似程度的反映，k 近邻空间选用欧式距离及更一般的 $L_p$ 距离。

设特征空间 X 是 n 维实数向量空间 $R^n$，$x_i,x_j\in \mathcal{X},x_i=(x_i^1,x_i^2,\cdots ,x_i^n),x_j=(x_j^1,x_j^2,\cdots ,x_j^n)$，则 $x_i,x_j$ 的$L_p$距离定义为:
$$L_p(x_i,x_j)={\left(\sum _{l=1}^n|x_i^l-x_j^l{|}^p\right)}^{\frac{1}{p}}$$

这里 p 要不小于1，当 p = 2时，成为欧氏距离；
当 p = 1 时，称为曼哈顿距离；
当 p = $\infty$ 时，它是各个坐标距离的最大值。

分类决策

k 近邻法中的分类决策规则往往是多数投票表决，即由输入实例的 k 个邻近的训练实例中的多数类决定输入实例的类。

多数表决规则（majorityvotingrule）有如下解释：如果分类的损失函数为 0-1 损失函数，分类函数为：
$$f:R^n\to \{c_1,c_2,\cdots ,c_K\}$$

那么对给定的实例 $x\in X$，其最近邻的 k 个训练实例点构成集合 $N_k(x$。如果涵盖$N_k(x)$的区域的类别是，那么误分类率是：
$$\frac{1}{k}\sum _{x_i\in N_k(x)}I(y_i\ne c_j)=1-\frac{1}{k}\sum _{x_i\in N_k(x)}I(y_i=c_j)$$

要使误分类率最小即经验风险最小，就要使${\sum }_{x_i\in N_k(x)}I(y_i=c_j)$最大，所以多数表决规则等价于经验风险最小化。

同时多数表决可以加权表决，可以一定程度提高表决结果的准确性。

k 近邻在手写数字识别上的实战

数据集的读取和解析和朴素贝叶斯法识别手写数字的原理一样，这里不再赘述。

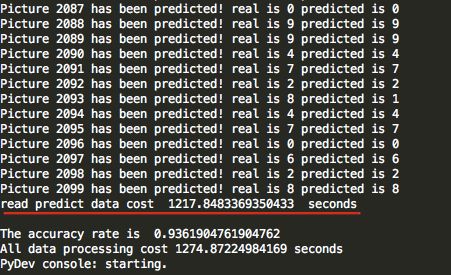
代码实现算法上，这里先采用线性暴搜的方法，效率上明显是非常低的，耗时也比朴素贝叶斯慢的多，但是准确率却非常高，目前表决数为 k=3 的情况下且不加权的预测准确率可以达到 94% 以上。

训练预测结果如下:

可以看出，测试 2100 个图片，用了1218秒，20多分钟，效率非常慢。

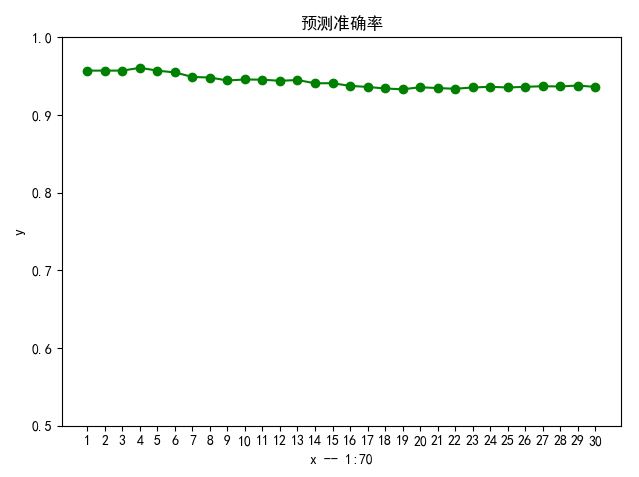
但是准确率异常高，且比较稳定。

总结

• 更高效率的 k 近邻寻找方法是 k-d树（k-dimensional树的简称），这是一种分割 k 维数据空间的数据结构，主要应用于多维空间关键数据的搜索。

• 可以对 k 近邻进行加权表决，对于预测准确率应该也会有所提升。

NEXT

下一次将实践以上的两点总结，看看具体的表现如何吧。

---

附KNN 算法的线性暴搜实现如下:

# -*- coding: utf-8 -*
import time
import matplotlib.pyplot as plt
import testLibrary as tl
import collections
import numpy as np

# 距离计算
def calc_dis(train_image,test_image):
    dist=np.linalg.norm(train_image-test_image)
    return dist


# 确定待分类实例的 k 近邻
def find_labels(k,train_images,train_labels,test_image):
    all_dis = []
    labels=collections.defaultdict(int)
    for i in range(len(train_images)):
        dis = np.linalg.norm(train_images[i]-test_image)
        all_dis.append(dis)
    sorted_dis = np.argsort(all_dis)
    count = 0
    while count < k:
        labels[train_labels[sorted_dis[count]]]+=1
        count += 1
    return labels


# 结合训练数据集，对所有待分类实例进行 k 近邻分类预测
def knn_all(k,train_images,train_labels,test_images, test_labels):
    print("start knn_all!")
    res=[]
    right = 0
    accuracy = []
    count=0
    for i in range(2100):
        labels=find_labels(k,train_images,train_labels,test_images[i])
        res.append(max(labels))
        print("Picture %d has been predicted! real is %d predicted is %d"%(count, test_labels[i], max(labels)))
        count+=1
        if max(labels) == test_labels[i]:
            right+=1
        if (i+1) % 70 == 0:
            accuracy.append(float(right)/(i+1))
    return res, accuracy


# 总的预测准确率计算
def calc_precision(res,test_labels):
    f_res_open=open("res.txt","a+")
    precision=0
    for i in range(len(res)):
        f_res_open.write("res:"+str(res[i])+"\n")
        f_res_open.write("test:"+str(test_labels[i])+"\n")
        if res[i]==test_labels[i]:
            precision+=1
    return precision/len(res)


if __name__ == '__main__':
    print('Start process train data')
    time_0 = time.time()
    # tl.get_train_set()

    print('Start process test data')
    time_t = time.time()
    # tl.get_test_set()

    # 读取训练数据集和测试数据集的方法和朴素贝叶斯方法一致
    print ('Start read train data')
    time_1 = time.time()
    data_map, labels = tl.loadCSVfile("data.csv")
    print(data_map.shape, labels.shape)
    time_2 = time.time()
    print('read data train cost ', time_2 - time_1, ' seconds', '\n')

    print('Start read predict data')
    time_3 = time.time()
    test_data_map, test_labels = tl.loadCSVfile("dataTest.csv")
    print(test_data_map.shape, test_data_map.shape)
    time_4 = time.time()
    print('read predict data cost ', time_4 - time_3, ' seconds', '\n')

    print('Start predicting data')
    time_5 = time.time()
    res, accuracy = knn_all(3, data_map, labels, test_data_map, test_labels)
    score = calc_precision(res, test_labels)
    time_6 = time.time()
    print('read predict data cost ', time_6 - time_5, ' seconds', '\n')

    new_ticks = np.linspace(1, 30, 30)
    plt.xticks(new_ticks)
    plt.ylim(ymin=0.5, ymax = 1)
    plt.plot(new_ticks, accuracy, 'o-', color='g')
    plt.xlabel("x -- 1:70")
    plt.ylabel("y")
    plt.title(u"预测准确率")
    plt.show()

    print("The accuracy rate is ", score)
    print("All data processing cost %s seconds" % (time_6 - time_0))