通过三个直观步骤理解ROC曲线
ROC曲线是一个分类模型效果好坏评判的的可视化表示。
在这篇文章中,我将分三个步骤头开始构建ROC曲线。
步骤1:获取分类模型预测
当我们训练一个分类模型时,我们得到得到一个结果的概率。在这种情况下,我们的例子将是偿还贷款的可能性。
概率通常在0到1之间。价值越高,这个人就越有可能偿还贷款。
下一步是找到一个临界值,将概率分类为“会偿还”或“不会偿还”。
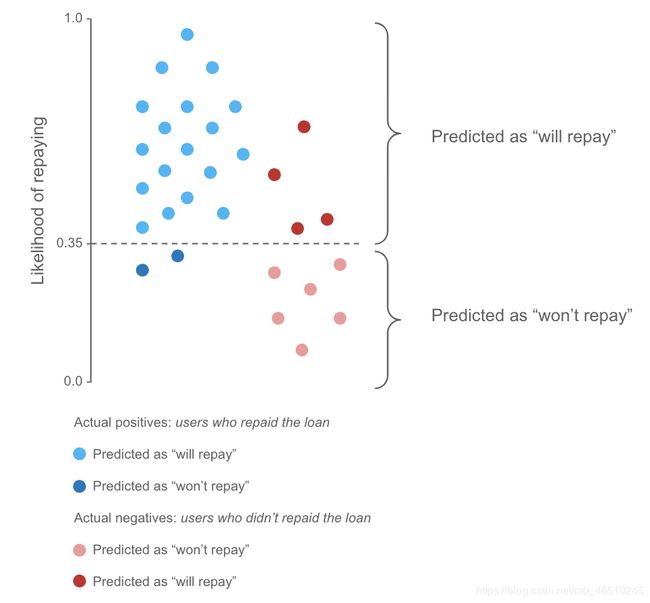
在图1的例子中,我们选择了0.35的阈值:
所有达到或超过这个门槛的预测,都被归类为“会偿还”
所有低于这个阈值的预测,被归类为“不会偿还”
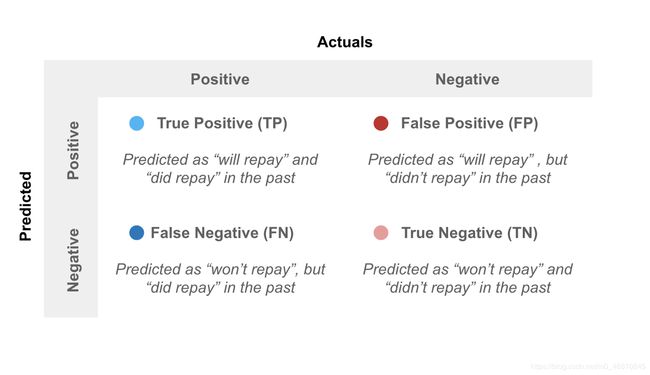
然后我们看看这些预测是正确的还是错误的。有了这些信息,我们可以建立一个混淆矩阵。
所有真正积极的方面,那些真正回报的人,都是蓝点。
如果他们被归类为“会偿还”,我们有一个真正的积极(TP)
如果他们被归类为“不会偿还”,我们就有了一个假阴性(FN)
所有的负的,那些没有偿还的,是红点。
如果他们被归类为“不会偿还”,我们就有了一个真正的负资产(TN)
如果他们被分类为“将偿还”,我们有一个假阳性(FP)
步骤2:计算真阳性率和假阳性率
到目前为止,我们已经对所有的预测进行了分类,我们知道这些分类是否正确。有了这些,我们将计算下面两个指标:
真阳性率(TPR):从过去所有“偿还”的人,我们正确分类的百分比是多少
假阳性率(FPR):从所有过去“没有偿还”的人,我们有多少百分比的错误分类
我们可以在图3中看到这些计算的公式。

下面,在图4的第二个图中,我们可以看到我们的原始示例在0.35的阈值处。此时,我们
正确分类90%的阳性,那些“回报”(TPR)
40%的负面评价,那些“没有偿还”的人(FPR)
我们可以看到,TPR和FPR的结果随着阈值的增大而降低。如果我们看第一个,阈值为0
所有阳性均正确分类,因此TPR = 100%
所有的阴性均被误分类,因此FPR = 100%
在最后一个图的例子中,阈值为1:
所有阳性均误诊,因此TPR = 0%
所有阴性均正确分类,因此FPR = 0%
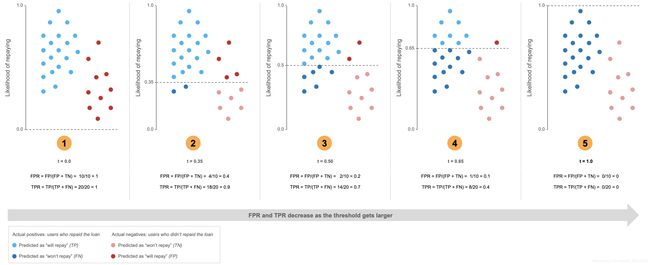
总的来说,我们可以看到这是一种取舍。当我们提高阈值时,我们会更好地对消极因素进行分类,但这是以错误地对更多积极因素进行分类为代价的
步骤3:绘制每个截止点的TPR和FPR
为了绘制ROC曲线,我们需要计算多个不同阈值的TPR和FPR(这一步包含在所有相关库中,如scikit-learn)。
对于每个阈值,我们在x轴上绘制FPR值,在y轴上绘制TPR值。然后我们用一条线把这些点连接起来。就是这样!
下面的图5中,我们可以看到ROC曲线上的每个点是如何代表某一分类在给定截断点处的FPR和TRP。
注意,1处的阈值是如何引出第一个点(0,0)而0处的阈值是如何引出最后一个点(1,1)的。
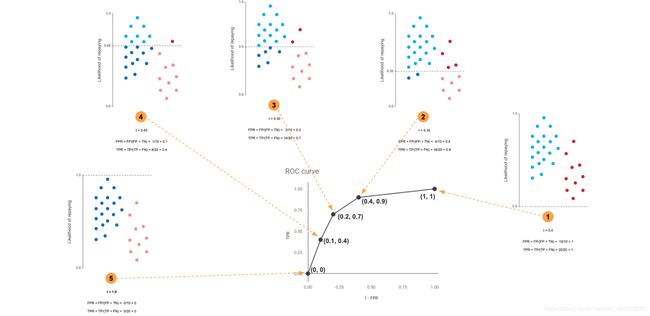
曲线下覆盖的面积称为曲线下面积(AUC)。这是用来评价一个分类模型的性能。AUC越高,模型在区分类方面就越好。
这意味着在一个理想的世界中,我们希望我们的线覆盖大部分左上方的图形,以获得更高的AUC。
作者:Valeria Cortez