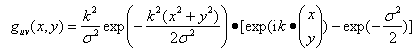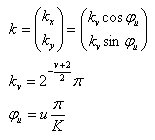Gabor滤波 + 多尺度问题
Gabor函数
Gabor变换属于加窗傅立叶变换,Gabor函数可以在频域不同尺度、不同方向上提取相关的特征。另外Gabor函数与人眼的生物作用相仿,所以经常用作纹理识别上,并取得了较好的效果。二维Gabor函数可以表示为:
其中:
v的取值决定了Gabor滤波的波长,u的取值表示Gabor核函数的方向,K表示总的方向数。参数![]() 决定了高斯窗口的大小,这里取
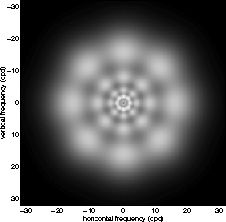
决定了高斯窗口的大小,这里取![]() 。程序中取4个频率(v=0, 1, ..., 3),8个方向(即K=8,u=0, 1, ... ,7),共32个Gabor核函数。不同频率不同方向的Gabor函数可通过下图表示:
。程序中取4个频率(v=0, 1, ..., 3),8个方向(即K=8,u=0, 1, ... ,7),共32个Gabor核函数。不同频率不同方向的Gabor函数可通过下图表示:
图片来源:GaborFilter.html
图片来源:http://www.bmva.ac.uk/bmvc/1997/papers/033/node2.html
参考:http://zhenyulu.cnblogs.com/articles/325968.html
网上有代码下载,蛮全的:http://download.csdn.net/detail/mathchunks/2740767
LOG(Laplacian-Gauss)
在图像中,边缘可以看做是位于一阶导数较大的像素处,因此,我们可以求图像的一阶导数来确定图像的边缘,像sobel算子等一系列算子都是基于这个思想的。但是这存在几个问题:1. 噪声的影响,在噪声点处一阶导数也会取极大值 2. 求解极大值的复杂性。所以,有了使用二阶导数的方法。这里主要考虑LoG算子,即高斯-拉普拉斯算子。
为什么要使用二阶导数呢?这里要考虑上面说的第二个问题,一阶导数的极大值到了二阶导数对应的值就是0了,很显然求解一个函数的零点值要比求极大值容易。这个性质也被称为二阶导数过零点(zero-crossing)。所以,我们就可以利用二阶导数来代替一阶导数了。而对于上面的第一个问题,也就是为什么要引入高斯算子的原因。
我们已经知道拉普拉斯算子其实就是一个二阶导数算子,为什么还要引入高斯呢?细想一下,高斯算子在图像处理中的一般的作用其实大都是进行模糊,换句话说它可以很好的抑制噪声,这样引入高斯算子我们就克服了噪声的影响(这也是LoG算子对拉普拉斯算子的改进的地方)。所以,高斯-拉普拉斯算子其实就是:先对图像进行高斯模糊,然后再求二阶导数,二阶导数等于0处对应的像素就是图像的边缘。
具体的推导过程可以看一下下面的链接:http://fourier.eng.hmc.edu/e161/lectures/gradient/node10.html
由于高斯函数的参数sigma对高斯算子的影响,所以,如果sigma选取的很小的话,前期的模糊效果很弱,也就可以近似等于拉普拉斯算子了。所以,拉普拉斯算子也可以看做高斯-拉普拉斯算子的一种极限情况。
LOG滤波器有以下特点:
(1)通过图象平滑,消除了一切尺度小于σ的图像强度变化;
(2)若用其它微分法,需要计算不同方向的微分,而它无方向性,因此可以节省计算量;
(3)它定位精度高,边缘连续性好,可以提取对比度较弱的边缘点。
LOG滤波器也有它的缺点:当边缘的宽度小于算子宽度时,由于过零点的斜坡融合将会丢失细节。LOG滤波器有无限长的拖尾,若取得很大尺寸,将使得计算不堪重负。但随着:r=的增加,LOG滤波器幅值迅速下降,当r大于一定程度时,可以忽略模板的作用,这就为节省计算量创造了条件。实际计算时,常常取n* n大小的LOG滤波器,近似n=3σ。另外,LOG滤波器可以近似为两个指数函数之差,即DOG ( Difference Of twoGaussians functions):当σ1/σ2=1.6时,DOG代替LOG减少了计算量。
参考:http://www.cnblogs.com/ztfei/archive/2012/09/01/2667050.html ;http://wenku.baidu.com/view/e47a421d6bd97f192279e97c.html
DOG(高斯差分)
进行高斯差分的结果是DOG(Difference of Gaussian),这个DOG是LOG(laplacian of Gaussian)的近似。LOG图像是目前来说尺度变换最好的,特精确。但是由于计算LOG图像很费劲,作者Lowe呢就对LOG图像进行了近似,他发现如果是用DOG的话呢,只和原来的LOG差了一个常数,这样的话最大值最小值的位置是不变的。而我们的目的呢,就是要找到这个最大最小值然后找到这个兴趣点的位置。关键是DOG计算起来很方便,只要两张图片相减就好了。
参考:http://zhidao.baidu.com/question/390079348.html
多尺度问题
1.采用DOG(高斯差分)来近似LOG算子, 其实直接计算LOG也是可以的;LOG算子是Laplace算子的扩展;laplace算子只能检测图像中的点;但是LOG不但可以检测局部极值点,还可以检测局部区域(斑点),这是因为高斯函数的核是可以变化的。用大的核检测出的局部极值点就是大的斑点。所以两幅图像若有相同的斑点,虽然大小不一,但采用不同和核是可以吧它们检测出来的。
2.通过上述的LOG算子,找到局部极值点,这就是Keypoints;
3.用大的核检测到的极值点,就在一个大的区域内计算局部梯度直方图, 用小的核检测到的极值点,就在一个小的区域内计算局部梯度直方图,
4.经过上述处理就可以进行点到点匹配啦; 其实主要的思想还是LOG算子的理解,它不仅仅是用来计算图像 的 边缘。