K均值聚类的理解和实现
目录
1. 距离的测度
1.1 欧式距离
1.2 马氏距离
1.2.1 利用马氏距离对数据进行归一化
1.2.2 利用马氏距离进行分类
2. K均值的基本理论
2.1 K均值的原理和实现
2.2 K均值的缺点
2.3 K均值改进
3. 算法实现
3.1 获取样本
3.2 协方差逆阵方根的计算方法
3.3 聚类实验
3.3.1 一般的K均值聚类
3.3.2 基于马氏距离K-means++聚类
3.3.3 基于肘部法则的K-means++聚类
4.参考资料
1. 距离测度
1.1 欧式距离
在数学中,欧氏距离或欧几里德度量是欧几里得空间中两点之间的“普通” 直线距离。通过这个距离,欧几里德空间成为度量空间。相关的规范称为欧几里得范数。较早的文献将度量指为毕达哥拉斯度量。广义的欧几里得范数项是L2范数或L2距离。
通常,对于n维空间来说,欧几里得距离可以表示为:
![]() 中的欧式距离如图1.1-1所示:
中的欧式距离如图1.1-1所示:
图1.1-1 ![]() 中欧几里得距离的表达
中欧几里得距离的表达
标准的欧几里德距离可以是平方的,以便逐渐将更大的重量放置在更远的物体上。在这种情况下,等式变为:
平方欧几里德距离不是一个度量,因为它不满足三角不等式 ; 然而,它经常用于仅需要比较距离的优化问题。
它在理性三角学领域也被称为quadrance。
1.2 马氏距离
马氏距离是对点P和分布D的距离度量。马氏距离对多维数据进行了归一化,并测量了P点相对于D的平均值的标准差。如果P在D分布中心,那么马氏距离为0。如果对数据进行主成分分析,如图1.2-1所示,那么,当P相对于主轴越远,马氏距离的数值也就随之增长。当我们对主轴进行进行归一化后,马氏距离也就等同于在欧式空间的仿射变换。因此,马氏距离具有“无单位”和“尺度不变性”的特性,并且考虑了数据集的相关性。
图1.2-1 数据的主成分分析
马哈拉诺比斯观察距离 :
从一组带有均值的观察中得出:
那么,观察值与集合的距离使用协方差矩阵S表示为:
集合中两个随机变量的距离为:
如果协方差矩阵是单位矩阵,则马哈拉诺比斯距离减小到欧几里得距离。如果协方差矩阵是对角矩阵,那么得到的距离度量称为标准欧式距离:
其中,![]() 表示变量
表示变量![]() 的标准差。
的标准差。
1.2.1 利用马氏距离进行数据归一化
如图1.2.1-1所示,当数据在空间中以非常不对称的形式进行分布时,k-means算法总是试图挖掘出一些与聚类相关的信息,因为k-means聚类的核心观点在于数据是以不均匀的方式进行聚类的。然而,“不对称”和“不均匀”之间却有着重要的区别。例如,当数据在某个维度上分布很远,而在其他维度上距离相对较小时,k-means必然不会收敛到好的结果。
图1.2.1-1 (a)原始数据的垂直距离比水平距离小 (b)对空间进行方差归一化,数据之间的水平距离小于垂直距离
这种情况往往只是因为数据向量在不同的维度有不同的底层单位。例如,如果使用身高、年龄和学龄代表一个人,那么由于单位的不同,数据在不同的维度上必然产生不同的分布。同样,年龄和学龄虽有着相同的单位,但是,在自然人口中也存在差异。
当我们将整个数据集作为一个整体来看待时,我们可以通过协方差矩阵来重新调整整个数据集,这种技术也称之为数据归一化。
传统意义上,马氏距离是以该点在特定的方向上的方差来度量数据点与分布之间的距离。我们使用分布的协方差的倒数来计算马氏距离:
其中, ![]() 表示数学期望,马氏距离可表示为:
表示数学期望,马氏距离可表示为:
对此有以下两种方式来解决:在K-means算法中使用马氏距离而不是欧式距离,或对数据进行尺度变化,然后在放缩的空间中使用欧几里得距离。第一种方法更为直观,但第二种方法更容易计算,因为数据转化是线性的。
数据集的转化:![]()
在这里,![]() 是即将使用的一组新的数据向量,D是原始数据。
是即将使用的一组新的数据向量,D是原始数据。![]() 的因子是逆协方差的平方根。
的因子是逆协方差的平方根。
1.2.2 利用马氏距离分类
利用K-means聚类或者任何其他的方法给定一组聚类标签,利用这些标签可以预测一些新的数据点最可能属于哪个聚类。假设聚类本身服从高斯分布,将马氏距离的概念引进该分类问题也是非常有意义的。
分类方法:对每个聚类计算平均协方差,这样我们可以基于协方差来计算新的数据点到每个聚类中心的马氏距离,从而确定分类。
但是,是不是说具有最小马氏距离的类是最优的解呢?
事实并非如此,当且仅当所有的聚类都拥有相同数量的数据点时(每个集群内的数据点的先验概率大小相等),此结论才成立。
贝叶斯规则简明扼要的说了这一区别:
对于给定的命题A和命题B,给定B的情况下,A发生的概率一般来说并不等于给定A的情况下,B发生的概率:
![]()
相反,给定A的情况下B发生的概率,乘以A的概率必然等于给定B的情况下A发生的概率诚意B发生的概率:
![]()
同样的道理,马氏距离表示的是一个特定样本来自特定聚类的概率,事实上,我们想知道的是:给定变量x,它出现在某一特定类中的概率。显然,马氏距离告诉我们的结论恰恰是相反的。例如,对于给定的变量x出现在C类的概率:
其中,![]() 表示聚类的数据量和整体数据里。
表示聚类的数据量和整体数据里。
也就是说,为了比较不同聚类的马氏聚类,我们必须考虑聚类的大小。考虑到每个聚类的概率服从高斯分布,聚类之间的似然性可以表示如下:
这就好比说,发现一只看似恐龙的蜥蜴属于恐龙的概率远远小于它属于蜥蜴的概率,正是因为两个集群的先验概率是不同的。
2. K均值的基本理论
2.1 K均值的基本原理和实现
K-means尝试寻找数据的自然类别,用户设置类别的个数,从而寻找到好的类别中心。
算法的流程如下:
1.输入数据集合和类别数K;
2.随机分配类别中心点的位置;
3.将每个点放入离它最近的类别中心点所在的集合;
4.移动类别中心点到它所在的集合;
5.转到第3步,直至收敛。
K均值的迭代示意图如图2.1-1所示:
图2.1-1 K均值的迭代示意图
2.2 K均值的缺点
K-means是一个极其高效的聚类算法,但是它存在以下三个问题:
1.它不能保证定位到聚类中心的最佳方案,但能保证收敛到某个解决方案;
2.K-means无法指出应该使用多少个类别。在同一数据集中,选择不同的类别得到的结果是不一样的,甚至是不合理的;
3.K-means假定空间的协方差矩阵不会影响到结果。
2.3 K-means的改进
1.多进行几次聚类,每次初始化的聚类中心不一样,最后选择方差最小的那个结果;
2.首先将类别设置为1,然后提高类别数(到达某个上限),一般情况下,总方差会快速下降直到达到某个拐点,这意味着再加一个新的聚类中心也不会显著减少总体方差。在拐点处停止,保存此时的类别数;
3.将数据乘以逆协方差矩阵进行数据的归一化。
3.算法实现
3.1获取样本
基本思路:利用随机数RNG函数算子对矩阵进行填充,这里采用了正态分布生成点集。
实现代码:
//定义实验允许的最大类别数
const int MAX_CLUSTERS = 5;
//定义数据点的颜色
Scalar colorTab[] = { Scalar(0,0,255),Scalar(0,255,0),Scalar(255,100,100),
Scalar(255,0,255),Scalar(0,255,255)};
//基于均匀分布生成随机的K值和样本数量
RNG rng(12345);
int k=rng.uniform(2, MAX_CLUSTERS);
int sampleCount = rng.uniform(100,1000);
Mat points(sampleCount, 1, CV_32FC2);
Mat lables;
Mat centers(k,1,CV_32FC1);
Mat img(500, 500,CV_8UC3);
//基于初始化的K值和sampleCount生成点集
for (int i = 0; i < k; i++)
{
//指定ROI
Mat pointChunk = points.rowRange(i*sampleCount/k,i==k-1?
sampleCount:(i+1)*sampleCount/k);
//基于正态分布填充ROI
rng.fill(pointChunk,RNG::NORMAL,Scalar(rng.uniform(0,img.cols),
rng.uniform(0,img.rows)),Scalar(img.cols*0.05, img.rows*0.05));
}
//打乱点的生成顺序
randShuffle(points,1,&rng);3.2 协方差逆阵平方根的计算方法
传统意义上,马氏距离是以该点在特定的方向上的方差来度量数据点与分布之间的距离。我们使用分布的协方差的倒数来计算马氏距离:
其中, ![]() 表示数学期望,马氏距离可表示为:
表示数学期望,马氏距离可表示为:
对此有以下两种方式来解决:在K-means算法中使用马氏距离而不是欧式距离,或对数据进行尺度变化,然后在放缩的空间中使用欧几里得距离。第一种方法更为直观,但第二种方法更容易计算,因为数据转化是线性的。
数据集的转化:![]()
在这里,![]() 是即将使用的一组新的数据向量,D是原始数据。
是即将使用的一组新的数据向量,D是原始数据。![]() 的因子是逆协方差的平方根。
的因子是逆协方差的平方根。
那么如何求解![]() 呢?
呢?
由于协方差矩阵是对称矩阵,基于特殊矩阵而言采用特征值分解的方法可以更准确的解出逆矩阵,现在我们假设![]() 已经求出,且有:
已经求出,且有:
由线性代数的基本理论知道,计算矩阵的幂的基本思想是对矩阵进行对角化,即:
![]()
当n=2时,只需要对特征向量计算平方,随后反乘特征向量S即可,计算代码如下:
//矩阵对角化计算A的平方
Mat A = (Mat_(4,4)<<0,1,1,-1,1,0,-1,1,1,-1,0,1,-1,1,1,0);
Mat value;
Mat vector;
bool M=eigen(A,value,vector);
Mat eigenValueMat= Mat::zeros(Size(value.rows,value.rows),CV_32FC1);
value.convertTo(value,CV_32FC1);
vector.convertTo(vector,CV_32FC1);
for (int i = 0; i < value.rows; i++)
{
eigenValueMat.at(i, i) = pow(value.at(i),2);
}
Mat eigenVectorMat;
transpose(vector, eigenVectorMat);
//对角化方法计算的解
Mat A_1 = eigenVectorMat*eigenValueMat* eigenVectorMat.inv();
//理论解
Mat A_2 = A*A;
//误差
Mat error = A_1 - A_2; 最终的误差矩阵error如图3.2-1所示:
图3.2-1 误差矩阵
显然,这个解是完全可以接受的。
3.3 聚类实验
3.3.1 一般的K均值聚类方法
在该条件下,对数据的样本点不加任何归一化处理,并基于已知的K值来对3.1中的样本进行聚类分析,实现的代码如下:
//1.一般的均值聚类
//1.1 直接调用聚类函数
kmeans(points,k,lables,TermCriteria(TermCriteria::EPS | TermCriteria::EPS,10,1.0),3,KMEANS_RANDOM_CENTERS,centers);
//1.2 绘制聚类结果
for (int i = 0; i < sampleCount; i++)
{
int colorIndex = lables.at(i);
Point pt = points.at(i);
circle(img,pt,2,colorTab[colorIndex],-1);
} 聚类的结果如下图3.3.1-1所示:
图3.3.1-1 一般的均值聚类
3.3.2 基于马氏距离k-means++的聚类方法的实现
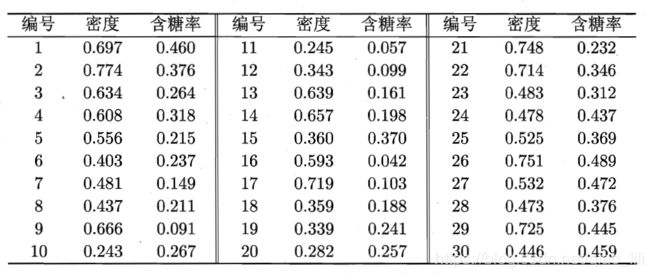
首先,为了创造马氏距离聚类的基本条件,在这里为了更好的可视化,数据采用二维矢量,但是在x和y两个维度上的服从不同的分布,为了使数据更具可信度,我参考了《机器学习》(周志华著)原型聚类章节里面的样本数据,如表3.3.2-1:
表3.3.2-1 西瓜数据集
其次,在原型聚类的实例中,书中给出的最终的迭代解,如图3.3.2-1所示:
图3.3.2-1 西瓜数据集均值聚类的结果
因此,为了方便进行数据实验,不妨设置聚类数目为k=3,实验的代码如下:
//2.基于马氏距离的k-means++聚类
//定义实验允许的最大类别数
const int MAX_CLUSTERS = 5;
//定义数据点的颜色
Scalar colorTab[] = { Scalar(0,0,255),Scalar(0,255,0),Scalar(255,100,100),Scalar(255,0,255),Scalar(0,255,255) };
//设置基本参数,k=3
RNG rng(12345);
int k = 3;
Mat lables;
Mat centers(k, 1, CV_32FC1);
Mat img(500, 500, CV_8UC3, Scalar(0));
Mat re_points = (Mat_(30, 2) << 0.697,0.460,0.774,0.376,0.634,0.264,0.608,0.318,0.556,
0.215,0.403,0.237,0.481,0.149,0.437,0.211,0.666,0.091,0.243,0.267,0.245,0.057,0.343,0.099,
0.639,0.161,0.657,0.198,0.360,0.370,0.593,0.042,0.719,0.103,0.359,0.188,0.339,0.241,0.282,
0.257,0.748,0.232,0.714,0.346,0.483,0.312,0.478,0.437,0.525,0.369,0.751,0.489,0.532,0.472,
0.473,0.376,0.725,0.445,0.446,0.459);
//求解协方差矩阵
Mat covar;
Mat mean;
calcCovarMatrix(re_points, covar,mean,CV_COVAR_NORMAL | CV_COVAR_ROWS);
//求解协方差的逆阵的方根
Mat covar_inv;
double inv=invert(covar,covar_inv,DECOMP_EIG);
Mat value;
Mat vector;
bool M = eigen(covar_inv, value, vector);
Mat eigenValueMat = Mat::zeros(Size(value.rows, value.rows), CV_32FC1);
value.convertTo(value,CV_32FC1);
vector.convertTo(vector, CV_32FC1);
for (int i = 0; i < value.rows; i++)
{
float tem = sqrt(value.at(i, 0));
eigenValueMat.at(i, i) = tem;
}
Mat eigenVectorMat;
transpose(vector, eigenVectorMat);
Mat result = eigenVectorMat*eigenValueMat* eigenVectorMat.inv();
//基于马氏距离进行归一化,重新生成点集
Mat New_points = re_points*result;
//聚类
kmeans(New_points, k, lables, TermCriteria(TermCriteria::EPS |
TermCriteria::EPS, 10, 1.0), 3, KMEANS_PP_CENTERS, centers);
for (int i = 0; i < 30; i++)
{
int colorIndex = lables.at(i);
int x = re_points.at(i, 0) * 500;
int y= 500-re_points.at(i, 1) * 500;
Point pt = Point(x,y);
circle(img, pt, 2, colorTab[colorIndex], -1);
} 最后,我想说的是k-means++与k-means方法最大的不同点在于中心的初始化方法,因为对于不同的初始点,聚类的结果必然会有差异,如果初始点选择的不好,那么极有可能陷入局部最小值下,从而得不到好的分类结果,而cv::KMEANS_PP_CENTERS选项会使cv::kmeans使用文献"Arthur, David, and S. Vassilvitskii. "k-means++: the advantages of careful seeding"中所谓的kmeans++的方法来重新分配聚类中心。这种方法谨慎的选择了聚类的中心起点,通常能以少于默认方法的迭代得出更好的结果。
上述代码的结果如图3.3.2-2所示:
图3.3.2-2 基于马氏距离的kmeans++聚类结果
3.3.3 基于肘部法则的K-means++聚类
如果问题中没有指定的值,可以通过肘部法则这一技术来估计聚类数量。肘部法则会把不同值的成本函数值画出来。随着值的增大,平均畸变程度会减小;每个类包含的样本数会减少,于是样本离其重心会更近。但是,随着值继续增大,平均畸变程度的改善效果会不断减低。值增大过程中,畸变程度的改善效果下降幅度最大的位置对应的值就是肘部。
在这里,我将畸变程度定义为所有类的样本点距该类中心的方差和。
考虑k从k=2到k=5逐步进行迭代,求解产生的畸变系数的程序如下:
//肘部法则的聚类
//定义实验允许的最大类别数
const int MAX_CLUSTERS = 5;
//定义数据点的颜色
Scalar colorTab[] = { Scalar(0,0,255),Scalar(0,255,0),Scalar(255,100,100),
Scalar(255,0,255),Scalar(0,255,255) };
//设置基本参数
RNG rng(12345);
int k;
Mat lables;
Mat img(500, 500, CV_8UC3, Scalar(0));
Mat points = (Mat_(30, 2) << 0.697, 0.460, 0.774, 0.376,
0.634, 0.264, 0.608, 0.318, 0.556,
0.215, 0.403, 0.237, 0.481, 0.149, 0.437, 0.211, 0.666,
0.091, 0.243, 0.267, 0.245, 0.057, 0.343, 0.099,
0.639, 0.161, 0.657, 0.198, 0.360, 0.370, 0.593, 0.042,
0.719, 0.103, 0.359, 0.188, 0.339, 0.241, 0.282,
0.257, 0.748, 0.232, 0.714, 0.346, 0.483, 0.312, 0.478,
0.437, 0.525, 0.369, 0.751, 0.489, 0.532, 0.472,
0.473, 0.376, 0.725, 0.445, 0.446, 0.459);
//定义方差
Mat varMat(5, 1, CV_32FC1, Scalar(0));
for (int k = 2; k <= MAX_CLUSTERS; k++)
{
Mat centers(k, 1, CV_32FC1);
kmeans(points, k, lables, TermCriteria(TermCriteria::EPS |
TermCriteria::EPS, 10, 1.0), 3, KMEANS_PP_CENTERS, centers);
vector sumVar(k, 0);
//统计每类点的数量
Mat lableCount(k, 1, lables.type(), Scalar(0));
for (int i = 0; i < 30; i++)
{
lableCount.at(lables.at(i)) += 1;
}
//计算方差
for (int i = 0; i < 30; i++)
{
int index = lables.at(i);
float x = points.at(i, 0);
float y = points.at(i, 1);
Point2f center = Point2f(centers.at(index, 0),
centers.at(index, 1));
sumVar[index] += ((x - center.x)*(x - center.x) +
(y - center.y)*(y - center.y)) / lableCount.at(index);
}
for (auto m : sumVar)
{
varMat.at(k - 2, 0) += m;
}
}
//数据归一化[0,500]
normalize(varMat,varMat,0,400,NORM_MINMAX);
//绘图
vector pts;
for (int i = 0; i < varMat.rows; i++)
{
Point tem;
tem.x = i*400/4+50;
tem.y = 450 - varMat.at(i);
pts.push_back(tem);
}
for (int i = 0; i < pts.size()-1;i++)
{
circle(img,pts[i],3,colorTab[i],-1);
}
line(img,pts[0],pts[1],Scalar(255,255,255));
line(img, pts[1], pts[2], Scalar(255, 255, 255));
line(img, pts[2], pts[3], Scalar(255, 255, 255)); 最终的结果如图3.3.3-1所示:
图3.3.3-1 基于肘部法则确定拐点
很显然,拐点发生在k=3的地方,因此最佳的聚类结果为k=3;
4.相关资料
1.OpenCV随机数发生器RNG:
《学习OpenCV3》:Page 157-161
2.对小矩阵使用逗号分隔式初始化函数:
《OpenCV编程入门》:Page 91
3.矩阵对角化理论、矩阵对角化Matlab实现:
https://blog.csdn.net/qq_18343569/article/details/49823441
https://blog.csdn.net/compression/article/details/49180775
4.聚类算法的一些思考:
https://blog.csdn.net/u013719780/article/details/51755124?utm_source=blogxgwz2
https://www.jianshu.com/p/95a4bcff2198
https://www.cnblogs.com/data-miner/p/6288227.html
5.原型聚类的基本理论:
《机器学习》-周志华:Page 202-211
6.维基百科:欧式距离与马氏距离
https://en.wikipedia.org/wiki/Euclidean_distance
https://en.wikipedia.org/wiki/Mahalanobis_distance