吴恩达机器学习课程笔记
目录
- 吴恩达机器学习课程笔记
- 机器学习定义
- 监督学习和无监督学习
- 单变量线性回归
- 模型表示(model representation)
- 代价函数
- 梯度下降
- 线性回归中的梯度下降
- 凸函数(convex function)
- 多变量线性回归
- 特征缩放(feature scaling)
- 学习率(learning rate)
- 特征和多项式回归
- 正规方程(normal equation)
- 逻辑回归(logistic regression)
- 假设表示
- 决策界限(Decision Boundary)
- 代价函数(cost function)
- 正则化(regularization)
- 欠拟合和过拟合(underfitting and overfitting)
- 欠拟合
- 过拟合
- 正则化代价函数
- 线性回归和逻辑回归的正则化
- 神经网络学习
- 模型表示
- 神经网络前向传播
- 代价函数
- 反向传播:
- 展开参数
- 梯度检验
- 随机初始化
- together
- 机器学习细节
- 模型选择(model selection)
- 方差和偏差(variance VS bias)
- 机器学习系统设计
- 不对称分类的误差评估(skewed classes)
- 查准率和召回率(Precision和Recall)
- 两者平衡
- PR曲线
- F1 Score
- 支持向量机
- 优化目标
- 间隔最大化
- 核函数
- SVM参数对性能的影响:
- 逻辑回归和SVM比较
- 无监督学习
吴恩达机器学习课程笔记
机器学习定义
什么是机器学习?
机器学习(Machine Learning):是研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能。一个程序被认为能从经验E中学习,解决任务 T,达到性能度量值P,当且仅当,有了经验E后,经过P评判, 程序在处理T时的性能有所提升。
监督学习和无监督学习
监督学习(Supervised Learning):对于数据集中每一个样本都有对应的标签,包括回归(regression)和分类(classification);
无监督学习(Unsupervised Learning):数据集中没有任何的标签,包括聚类(clustering),著名的一个例子是鸡尾酒晚会。实现公式:[W,s,v] = svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x’);
单变量线性回归
模型表示(model representation)
线性回归模型:
h θ ( x ) = θ 0 + θ 1 x J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h ( x i ) − y i ) 2 h_\theta(x)=\theta_0+\theta_1x \\ J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(h(x^i)-y^i)^2 hθ(x)=θ0+θ1xJ(θ0,θ1)=2m1i=1∑m(h(xi)−yi)2给定训练样本 ( x i , y i ) (x^i,y^i) (xi,yi),其中: i = 1 , 2 , . . . , m i=1,2,...,m i=1,2,...,m, x x x表示特征, y y y表示输出目标,监督学习算法的工作方式如图所示:
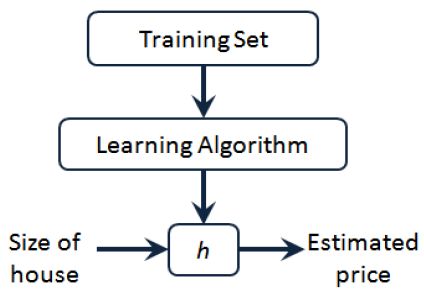
假设函数h(hypothesis):是一个从输入 x x x到输出 y y y的映射, h ( x ) = θ 0 + θ 1 x h(x)=\theta_0+\theta_1x h(x)=θ0+θ1x。 θ 0 \theta_0 θ0和 θ 1 \theta_1 θ1都是模型参数。
代价函数
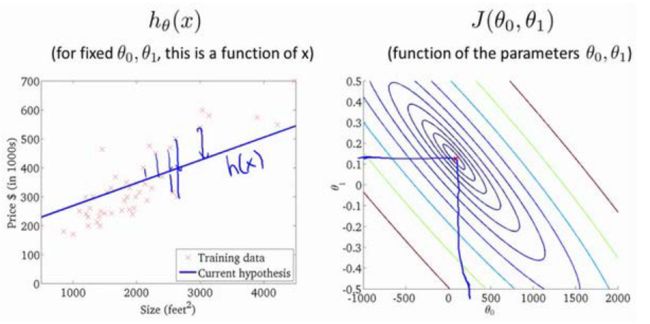
代价函数(cost function) J ( θ ) J(\theta) J(θ),通常使用平方误差函数,如下: J ( θ 0 , θ 1 ) = 1 2 m ∑ i = 1 m ( h ( x i ) − y i ) 2 , m 为 训 练 样 本 的 数 量 。 J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(h(x^i)-y^i)^2,m为训练样本的数量。 J(θ0,θ1)=2m1i=1∑m(h(xi)−yi)2,m为训练样本的数量。训练的目标为最小化代价函数,即 m i n m i z e θ 0 , θ 1 J ( θ 0 , θ 1 ) \underset {\theta_0,\theta_1} {minmize}J(\theta_0,\theta_1) θ0,θ1minmizeJ(θ0,θ1)。
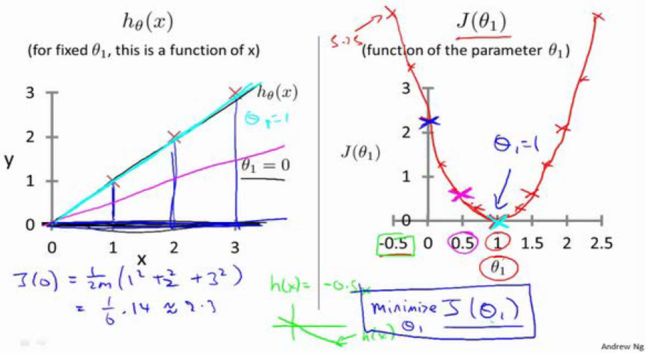
代价函数的另外一个图形表示是等高图,如图所示:
梯度下降
代价函数: J ( θ 0 , θ 1 ) J(\theta_0,\theta_1) J(θ0,θ1),可以推广到 J ( θ 0 , θ 1 , θ 2 , . . . , θ n ) J(\theta_0,\theta_1,\theta_2,...,\theta_n) J(θ0,θ1,θ2,...,θn)
目标: m i n θ 0 , θ 1 J ( θ 0 , θ 1 ) \underset {\theta_0,\theta_1} {min}J(\theta_0,\theta_1) θ0,θ1minJ(θ0,θ1)
初始化 θ 0 , θ 1 \theta_0,\theta_1 θ0,θ1,更新公式: θ j = θ j − α ∂ ∂ θ j J ( θ 0 , θ 1 ) \theta_j=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1) θj=θj−α∂θj∂J(θ0,θ1) α \alpha α为学习速率(learning rate)。
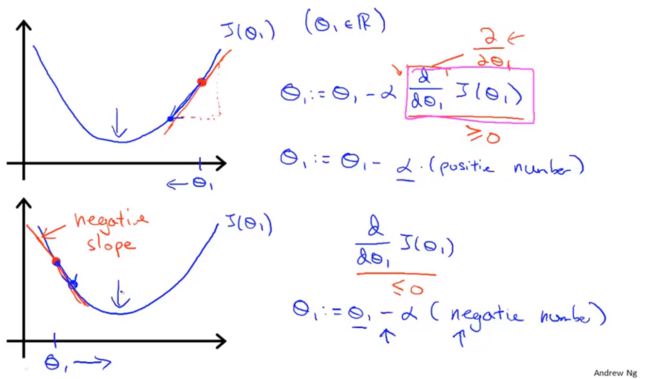
如果α太小,梯度下降会变得缓慢;如果α太大,梯度下降可能无法收敛甚至发散。
线性回归中的梯度下降
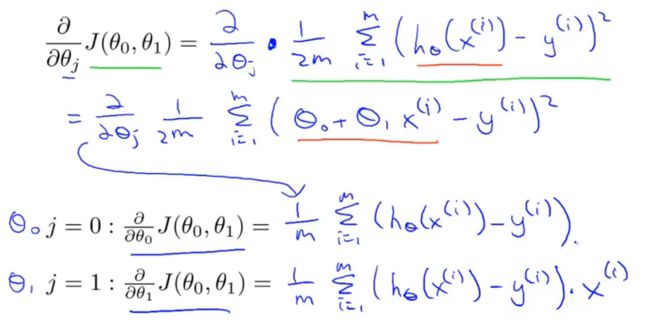
梯度下降的每一步遍历的所有数据集中的样例,又叫“batch” Gradient Descent Algorithm。
凸函数(convex function)
多变量线性回归
假设函数: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+\dots+\theta_nx_n hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn。 定义 x 0 = 1 x_0=1 x0=1,
从而: x = [ x 0 , x 1 , x 2 , … , x n ] T , x ∈ R n + 1 x=[x_0,x_1,x_2,\dots,x_n]^T,x\in\R^{n+1} x=[x0,x1,x2,…,xn]T,x∈Rn+1; θ = [ θ 0 , θ 1 , θ 2 , … , θ n ] T , θ ∈ R n + 1 \theta=[\theta_0,\theta_1,\theta_2,\dots,\theta_n]^T,\theta\in\R^{n+1} θ=[θ0,θ1,θ2,…,θn]T,θ∈Rn+1
假设函数可记作: h θ ( x ) = θ T x h_\theta(x)=\theta^Tx hθ(x)=θTx。
代价函数: J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2 J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2梯度下降更新公式: θ j : = θ j − α ∂ ∂ θ j J ( θ ) , j = 0 , 1 , … , n \theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta),\ j=0,1,\dots,n θj:=θj−α∂θj∂J(θ), j=0,1,…,n更精确的: θ j : = θ j − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) , j = 0 , 1 , … , n \theta_j:=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)},\ j=0,1,\dots,n θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))xj(i), j=0,1,…,n
可以通过for循环更新 θ \theta θ,也可以采用向量形式更新 θ \theta θ: θ = θ − α m X T ( X θ − y ) \theta=\theta-\frac{\alpha}{m}X^T(X\theta-y) θ=θ−mαXT(Xθ−y)
特征缩放(feature scaling)
目的:保证特征处于相似的尺度上,有利于加快梯度下降算法运行速度,加快收敛到全局最小值
方式:
Mean normalization: x i = x i − μ σ x_i=\frac{x_i-\mu}{\sigma} xi=σxi−μ其中 μ \mu μ为平均值, σ \sigma σ为标准差;
max-min: x i = x i − m i n m a x − m i n x_i=\frac{x_i-min}{max-min} xi=max−minxi−min
学习率(learning rate)
梯度下降更新公式: θ j : = θ j − α ∂ ∂ θ j J ( θ ) , \theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta), θj:=θj−α∂θj∂J(θ),
- “debugging”:如何确保梯度下降正确运行;
- 如何正确选择学习率。
- 如果 α \alpha α太小:收敛慢
- 如果 α \alpha α太大:每一次迭代过程中 J ( θ ) J(\theta) J(θ)将会不断的越过最小值,无法收敛, J ( θ ) J(\theta) J(θ)如下图所示:
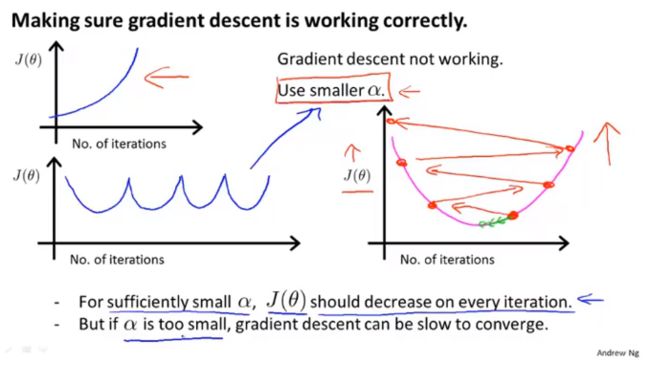
- choose α \alpha α: … , 0.001 , 0.003 , 0.01 , 0.03 , 0.1 , 0.3 , 1 , … \dots,0.001,0.003,0.01,0.03,0.1,0.3,1,\dots …,0.001,0.003,0.01,0.03,0.1,0.3,1,…
- 寻找一个合适的较小值和较大值,保证结果和速度的同时选取较大的值,或者稍小的合理值。
特征和多项式回归
举例:房价预测问题
假设有两个特征: x 1 x_1 x1是土地宽度, x 2 x_2 x2是土地纵向深度,可做假设: h θ ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2 hθ(x)=θ0+θ1x1+θ2x2。
可以考虑构造特征底面积 x = x 1 ∗ x 2 x=x_1*x_2 x=x1∗x2,此时假设函数: h θ ( x ) = θ 0 + θ 1 x h_\theta(x)=\theta_0+\theta_1x hθ(x)=θ0+θ1x。
数据集样本分布如图:
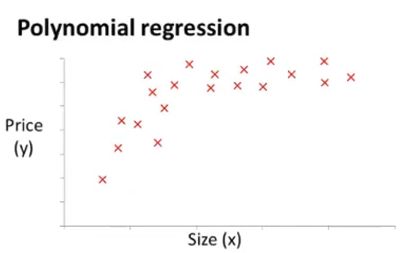
多项式回归(polynomial regression):
二次模型:
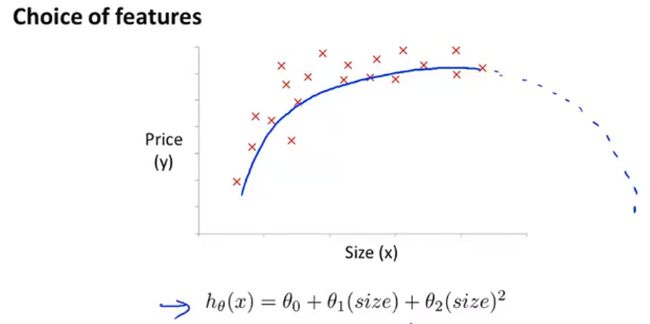
三次模型:
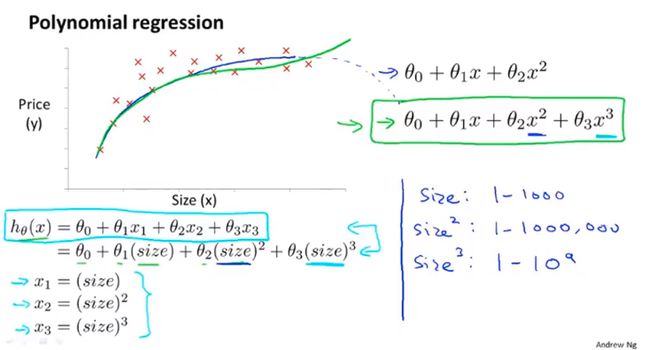
更恰当的模型:

正规方程(normal equation)
代价函数: J ( θ ) = 1 2 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2 J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2对 J ( θ ) J(\theta) J(θ)求偏导并令导数为零可解得: θ = ( X T X ) − 1 X T y \theta=(X^TX)^{-1}X^Ty θ=(XTX)−1XTy,推导过程如下:
令 x ( i ) = ( x 0 ( i ) x 1 ( i ) ⋮ x n ( i ) ) ∈ R n + 1 , y = ( y 1 y 2 ⋮ y m ) ∈ R m x^{(i)}=\begin{pmatrix}x_0^{(i)}\\x_1^{(i)}\\\vdots\\x_n^{(i)}\\\end{pmatrix}\in\R^{n+1},y=\begin{pmatrix}y_1\\y_2\\\vdots\\y_m\\\end{pmatrix}\in\R^m x(i)=⎝⎜⎜⎜⎜⎛x0(i)x1(i)⋮xn(i)⎠⎟⎟⎟⎟⎞∈Rn+1,y=⎝⎜⎜⎜⎛y1y2⋮ym⎠⎟⎟⎟⎞∈Rm令
X = ( 1 x 1 ( 1 ) ⋯ x j ( 1 ) ⋯ x n ( 1 ) 1 x 1 ( 2 ) ⋯ x j ( 2 ) ⋯ x n ( 2 ) ⋮ ⋮ ⋱ ⋮ ⋱ ⋮ 1 x 1 ( m ) ⋯ x j ( m ) ⋯ x n ( m ) ) = ( ( x ( 1 ) ) T ( x ( 2 ) ) T ⋮ ( x ( m ) ) T ) ∈ R m × ( n + 1 ) X=\begin{pmatrix} 1 & x_1^{(1)} & \cdots & x_j^{(1)} & \cdots & x_n^{(1)} \\ 1 & x_1^{(2)} & \cdots & x_j^{(2)} & \cdots & x_n^{(2)} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots \\ 1 & x_1^{(m)} & \cdots & x_j^{(m)} & \cdots & x_n^{(m)} \\ \end{pmatrix} =\begin{pmatrix} (x^{(1)})^T\\(x^{(2)})^T\\\vdots\\(x^{(m)})^T \end{pmatrix}\in\R^{m×(n+1)} X=⎝⎜⎜⎜⎜⎛11⋮1x1(1)x1(2)⋮x1(m)⋯⋯⋱⋯xj(1)xj(2)⋮xj(m)⋯⋯⋱⋯xn(1)xn(2)⋮xn(m)⎠⎟⎟⎟⎟⎞=⎝⎜⎜⎜⎛(x(1))T(x(2))T⋮(x(m))T⎠⎟⎟⎟⎞∈Rm×(n+1)又 ∂ ∂ θ J ( θ ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x ( i ) = 0 \frac{\partial}{\partial\theta}J(\theta)=\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x^{(i)}=0 ∂θ∂J(θ)=m1∑i=1m(hθ(x(i))−y(i))x(i)=0,可得 θ = ( X T X ) − 1 X T y \theta = (X^TX)^{-1}X^Ty θ=(XTX)−1XTy推导过程如下:

正规方程存在条件:
- X T X X^TX XTX是可逆矩阵,若不可逆,可计算广义可逆矩阵。

比较:
梯度下降算法:需要选择学习速率 α \alpha α; 需要许多次迭代;当特征数量n较大时也能够运转正常;
正规方程: 无需选择参数;无需迭代;需要计算 ( X T X ) − 1 (X^TX)^{-1} (XTX)−1;当n较大时计算缓慢
逻辑回归(logistic regression)
假设表示
逻辑回归模型: h θ ( x ) , h_\theta(x), hθ(x),want: 0 ≤ h θ ( x ) ≤ 1 0 \leq h_\theta(x) \leq 1 0≤hθ(x)≤1
令 h θ ( x ) = g ( θ T x ) \ h_\theta(x)\ =g(\theta^Tx) hθ(x) =g(θTx),将 θ T x \theta^Tx θTx代入 g ( ⋅ ) g(\cdot) g(⋅): h θ ( x ) = 1 1 + e − θ T x h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}} hθ(x)=1+e−θTx1其中: g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1称为Sigmod函数,也叫作Logistic函数。
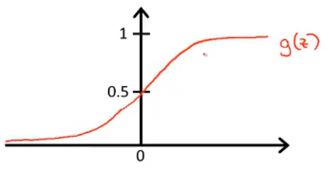
hope:
{ h θ ( x ) ≥ 0.5 , y = 1 h θ ( x ) < 0.5 , y = 0 \begin{cases} h_\theta(x) \geq 0.5,y=1 \\ h_\theta(x) < 0.5,y=0 \end{cases} {hθ(x)≥0.5,y=1hθ(x)<0.5,y=0
从概率的角度: h θ ( x ) = p { y = 1 ∣ x , θ } h_\theta(x)=p\{y=1|x,\theta\} hθ(x)=p{y=1∣x,θ}
决策界限(Decision Boundary)
predict:y=1 , if h θ ( x ) ≥ 0.5 \text {predict:y=1},\text {if }h_\theta(x) \geq 0.5 predict:y=1,if hθ(x)≥0.5
predict:y=0 , if h θ ( x ) < 0.5 \text {predict:y=0},\text {if }h_\theta(x) < 0.5 predict:y=0,if hθ(x)<0.5
h θ ( x ) ≥ 0.5 → z ≥ 0 → θ T x ≥ 0 h_\theta(x) \geq 0.5\quad \to\quad z\geq0 \quad \to\quad \theta^Tx\geq0 hθ(x)≥0.5→z≥0→θTx≥0
h θ ( x ) < 0.5 → z < 0 → θ T x < 0 h_\theta(x) < 0.5\quad \to\quad z<0 \quad \to\quad \theta^Tx<0 hθ(x)<0.5→z<0→θTx<0
定义: θ T x = 0 \theta^Tx=0 θTx=0为决策边界。
代价函数(cost function)
假设表示定义的: h θ ( x ) = p { y = 1 ∣ x , θ } h_\theta(x)=p\{y=1|x,\theta\} hθ(x)=p{y=1∣x,θ},由极大似然的思想: θ = a r g m a x θ ∏ i = 1 m p { y i = 1 ∣ x , θ } y i p { y i = 0 ∣ x , θ } 1 − y i = a r g m a x θ ∏ i = 1 m p { y i = 1 ∣ x , θ } y i ( 1 − p { y i = 1 ∣ x , θ } ) 1 − y i \begin{array}{} \theta=\underset{\theta}{argmax}\prod_{i=1}^{m}p\{y_i=1|x,\theta\}^{y_i}p\{y_i=0|x,\theta\}^{1-y_i}\\ = \underset{\theta}{argmax}\prod_{i=1}^{m}p\{y_i=1|x,\theta\}^{y_i}(1-p\{y_i=1|x,\theta\})^{1-y_i} \end{array}{} θ=θargmax∏i=1mp{yi=1∣x,θ}yip{yi=0∣x,θ}1−yi=θargmax∏i=1mp{yi=1∣x,θ}yi(1−p{yi=1∣x,θ})1−yi令 Γ = ∏ i = 1 m p { y i = 1 ∣ x , θ } y i ( 1 − p { y i = 1 ∣ x , θ } ) 1 − y i \Gamma=\prod_{i=1}^{m}p\{y_i=1|x,\theta\}^{y_i}(1-p\{y_i=1|x,\theta\})^{1-y_i} Γ=∏i=1mp{yi=1∣x,θ}yi(1−p{yi=1∣x,θ})1−yi,取对数可得: log ( Γ ) = ∑ i = 1 m y i log ( h θ ( x ) ) + ( 1 − y i ) ( 1 − log ( h θ ( x ) ) ) \log(\Gamma)=\sum_{i=1}^my_i\log(h_\theta(x))+(1-y_i)(1-\log(h_\theta(x))) log(Γ)=i=1∑myilog(hθ(x))+(1−yi)(1−log(hθ(x)))所以: θ = a r g m a x θ log ( Γ ) = a r g m a x θ ∑ i = 1 m y i log ( h θ ( x ) ) + ( 1 − y i ) ( 1 − log ( h θ ( x ) ) ) \theta = \underset{\theta}{argmax}\log(\Gamma)\\=\underset{\theta}{argmax}\sum_{i=1}^my_i\log(h_\theta(x))+(1-y_i)(1-\log(h_\theta(x))) θ=θargmaxlog(Γ)=θargmaxi=1∑myilog(hθ(x))+(1−yi)(1−log(hθ(x)))令 c o s t ( h θ ( x ) , y i ) = − y i log ( h θ ( x ) ) − ( 1 − y i ) ( 1 − log ( h θ ( x ) ) ) cost(h_\theta(x),y_i)=-y_i\log(h_\theta(x))-(1-y_i)(1-\log(h_\theta(x))) cost(hθ(x),yi)=−yilog(hθ(x))−(1−yi)(1−log(hθ(x))),所以目标: θ = a r g m a x θ ∑ i = 1 m c o s t ( h θ ( x ) , y i ) \theta= \underset{\theta}{argmax}\sum_{i=1}^mcost(h_\theta(x),y_i) θ=θargmaxi=1∑mcost(hθ(x),yi)(注意:线性回归的 c o s t ( h θ ( x ) , y i ) = ( h θ ( x ) − y i ) 2 cost(h_\theta(x),y_i)=(h_\theta(x)-y_i)^2 cost(hθ(x),yi)=(hθ(x)−yi)2。)
由于 c o s t ( h θ ( x ) , y i ) = − y i log ( h θ ( x ) ) − ( 1 − y i ) ( 1 − log ( h θ ( x ) ) ) cost(h_\theta(x),y_i)=-y_i\log(h_\theta(x))-(1-y_i)(1-\log(h_\theta(x))) cost(hθ(x),yi)=−yilog(hθ(x))−(1−yi)(1−log(hθ(x))),写成: c o s t ( h θ ( x ) , y i ) = { − y i log ( h θ ( x ) ) , if y i = 1 − ( 1 − y i ) ( 1 − log ( h θ ( x ) ) ) , if y i = 0 cost(h_\theta(x),y_i)=\begin{cases} -y_i\log(h_\theta(x)),\quad \quad \quad \quad\quad\text{if $y_i=1$} \\-(1-y_i)(1-\log(h_\theta(x))),\text{if $y_i=0$}\end{cases} cost(hθ(x),yi)={−yilog(hθ(x)),if yi=1−(1−yi)(1−log(hθ(x))),if yi=0
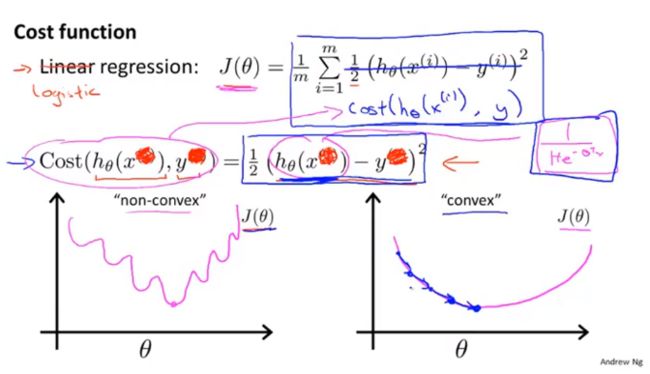

逻辑回归代价函数:
J ( θ ) = 1 m ∑ i = 1 m c o s t ( h θ ( x ( i ) ) , y ( i ) ) = − 1 m ∑ i = 1 m ( y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ) J(\theta)=\frac{1}{m}\sum_{i=1}^{m}cost(h_\theta(x^{(i)}),y^{(i)})\\=-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}\log(h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))) J(θ)=m1i=1∑mcost(hθ(x(i)),y(i))=−m1i=1∑m(y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i))))拟合参数: min θ J ( θ ) \underset{\theta}{\min}J(\theta) θminJ(θ)
梯度下降法:
∂ ∂ θ j J ( θ ) = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial}{\partial\theta_j}J(\theta)=\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} ∂θj∂J(θ)=m1i=1∑m(hθ(x(i))−y(i))xj(i) θ j : = θ j − α ∂ ∂ θ j J ( θ ) = θ j − α m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j:=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta)=\theta_j-\frac{\alpha}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} θj:=θj−α∂θj∂J(θ)=θj−mαi=1∑m(hθ(x(i))−y(i))xj(i)高级优化算法:
- 共轭梯度算法
- BFGS
- L-BFGS
优点:无需人工选择参数 α \alpha α;运算速度比梯度下降更快
缺点:更加复杂
正则化(regularization)
欠拟合和过拟合(underfitting and overfitting)
欠拟合
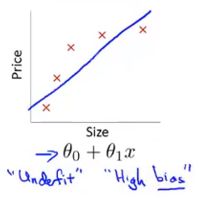
欠拟合,高偏差:说明没有很好的拟合训练数据
解决办法:增加特征,如增加多项式
过拟合
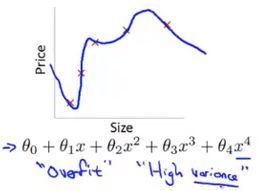
过拟合,高方差:拟合训练数据过于完美, J ( θ ) ≈ 0 J(\theta)\approx0 J(θ)≈0,导致模型的泛化能力很差,对于新样本不能准确预测;
解决办法:
- 减少特征个数
a)人工保留合适的特征
b)采用模型选择算法 - 正规化
a)保留所有特征,减小参数 θ j \theta_j θj的维度
正则化代价函数
对 θ j \theta_j θj加入惩罚项:
线性回归代价函数: J ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 m θ j 2 ] J(\theta)=\frac{1}{2m}\left[ \sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^m\theta_j^2\right] J(θ)=2m1[i=1∑m(hθ(x(i))−y(i))2+λj=1∑mθj2]
逻辑回归代价函数:
J ( θ ) = − 1 m ∑ i = 1 m ( y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ) + λ 2 m ∑ j = 1 m θ j 2 J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}\log(h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)})))+\frac{\lambda}{2m}\sum_{j=1}^{m}\theta_j^2 J(θ)=−m1i=1∑m(y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i))))+2mλj=1∑mθj2拟合参数: min θ J ( θ ) \underset{\theta}{\min}J(\theta) θminJ(θ)目标: min θ J ( θ ) \underset{\theta}{\min}J(\theta) θminJ(θ)
线性回归和逻辑回归的正则化
梯度下降算法:
repeat:{ θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) \theta_0:= \theta_0-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)} θ0:=θ0−αm1i=1∑m(hθ(x(i))−y(i))x0(i) θ j : = θ j − α 1 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) + λ θ j ] \theta_j:= \theta_j-\alpha\frac{1}{m}\left[\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)}+\lambda\theta_j\right] θj:=θj−αm1[i=1∑m(hθ(x(i))−y(i))x0(i)+λθj]
\quad\quad\quad\; }
等价于:
repeat:{ θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) \theta_0:= \theta_0-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)} θ0:=θ0−αm1i=1∑m(hθ(x(i))−y(i))x0(i) θ j : = θ j ( 1 − α 1 m ) − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x 0 ( i ) \theta_j:= \theta_j(1-\alpha\frac{1}{m})-\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)} θj:=θj(1−αm1)−αm1i=1∑m(hθ(x(i))−y(i))x0(i)
\quad\quad\quad\; }
正规方程:
假设: m ≤ n ( e x a m p l e s ≤ f e a t u r e s ) m\leq n(examples\leq features) m≤n(examples≤features)
θ = ( X T X ) − 1 X T y \theta=(X^TX)^{-1}X^Ty θ=(XTX)−1XTyIf λ > 0 \lambda>0 λ>0, θ = ( X T X + λ [ 0 1 1 ⋱ 1 ] ⎵ ( n + 1 ) × ( n + 1 ) ) − 1 X T y \theta=\left(X^TX+\lambda\underbrace{ \begin{bmatrix}0\\ &1\\ &&1\\ &&& \ddots \\&&&&1\end{bmatrix}}_{(n+1)\times(n+1)}\right)^{-1}X^Ty θ=⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛XTX+λ(n+1)×(n+1) ⎣⎢⎢⎢⎢⎡011⋱1⎦⎥⎥⎥⎥⎤⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞−1XTy只要 λ > 0 \lambda>0 λ>0,那么括号内的矩阵一定不是奇异矩阵,也就是可逆的。
神经网络学习
模型表示
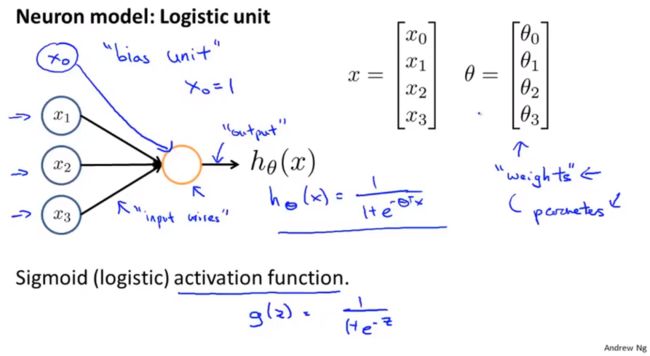
上图代表单个的神经元。神经网络即是一组神经元。典型的三层神经网络如下图所示:

详细解释:
a i ( j ) a^{(j)}_i ai(j):第 j j j层的单元 i i i的激活项。(“activation of unit i in layer j”)
Θ ( j ) \Theta^{(j)} Θ(j):从第 j j j层( u n i t s units units: s j s_j sj)到第 j + 1 j+1 j+1层( u n i t s units units: s j + 1 s_{j+1} sj+1)的权重矩阵,维数: s j + 1 × ( s j + 1 ) s_{j+1}\times (s_j+1) sj+1×(sj+1)
a 1 ( 2 ) = g ( Θ 10 ( 1 ) x 0 + Θ 11 ( 1 ) x 1 + Θ 12 ( 1 ) x 2 + Θ 13 ( 1 ) x 3 ) a_1^{(2)}=g(\Theta_{10}^{(1)}x_0+\Theta_{11}^{(1)}x_1+\Theta_{12}^{(1)}x_2+\Theta_{13}^{(1)}x_3) a1(2)=g(Θ10(1)x0+Θ11(1)x1+Θ12(1)x2+Θ13(1)x3) a 2 ( 2 ) = g ( Θ 20 ( 1 ) x 0 + Θ 21 ( 1 ) x 1 + Θ 22 ( 1 ) x 2 + Θ 23 ( 1 ) x 3 ) a_2^{(2)}=g(\Theta_{20}^{(1)}x_0+\Theta_{21}^{(1)}x_1+\Theta_{22}^{(1)}x_2+\Theta_{23}^{(1)}x_3) a2(2)=g(Θ20(1)x0+Θ21(1)x1+Θ22(1)x2+Θ23(1)x3) a 3 ( 2 ) = g ( Θ 30 ( 1 ) x 0 + Θ 31 ( 1 ) x 1 + Θ 32 ( 1 ) x 2 + Θ 33 ( 1 ) x 3 ) a_3^{(2)}=g(\Theta_{30}^{(1)}x_0+\Theta_{31}^{(1)}x_1+\Theta_{32}^{(1)}x_2+\Theta_{33}^{(1)}x_3) a3(2)=g(Θ30(1)x0+Θ31(1)x1+Θ32(1)x2+Θ33(1)x3) h Θ ( x ) = a 1 ( 3 ) = g ( Θ 10 ( 2 ) a 0 ( 2 ) + Θ 11 ( 2 ) a 1 ( 2 ) + Θ 12 ( 2 ) a 2 ( 2 ) + Θ 13 ( 2 ) a 3 ( 2 ) ) h_\Theta(x)=a_1^{(3)}=g(\Theta_{10}^{(2)}a_0^{(2)}+\Theta_{11}^{(2)}a_1^{(2)}+\Theta_{12}^{(2)}a_2 ^{(2)}+\Theta_{13}^{(2)}a_3^{(2)}) hΘ(x)=a1(3)=g(Θ10(2)a0(2)+Θ11(2)a1(2)+Θ12(2)a2(2)+Θ13(2)a3(2))
神经网络前向传播
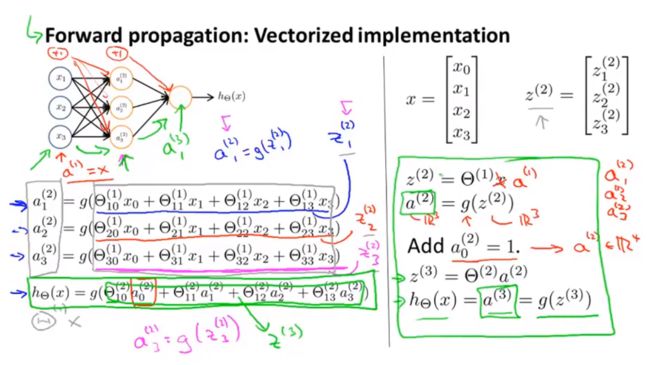 h Θ ( x ) = a ( 3 ) = g ( z ( 3 ) ) = g ( Θ ( 2 ) a ( 2 ) ) = g ( Θ ( 2 ) g ( z ( 2 ) ) ) = g ( Θ ( 2 ) g ( Θ ( 1 ) a ( 1 ) ) ) h_\Theta(x)=a^{(3)}=g(z^{(3)})=g(\Theta^{(2)}a^{(2)})=g(\Theta^{(2)}g(z^{(2)}))=g(\Theta^{(2)}g(\Theta^{(1)}a^{(1)})) hΘ(x)=a(3)=g(z(3))=g(Θ(2)a(2))=g(Θ(2)g(z(2)))=g(Θ(2)g(Θ(1)a(1)))
h Θ ( x ) = a ( 3 ) = g ( z ( 3 ) ) = g ( Θ ( 2 ) a ( 2 ) ) = g ( Θ ( 2 ) g ( z ( 2 ) ) ) = g ( Θ ( 2 ) g ( Θ ( 1 ) a ( 1 ) ) ) h_\Theta(x)=a^{(3)}=g(z^{(3)})=g(\Theta^{(2)}a^{(2)})=g(\Theta^{(2)}g(z^{(2)}))=g(\Theta^{(2)}g(\Theta^{(1)}a^{(1)})) hΘ(x)=a(3)=g(z(3))=g(Θ(2)a(2))=g(Θ(2)g(z(2)))=g(Θ(2)g(Θ(1)a(1)))
代价函数
逻辑回归代价函数: J ( θ ) = − 1 m ∑ i = 1 m ( y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ) + λ 2 m ∑ j = 1 m θ j 2 J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}\log(h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)})))+\frac{\lambda}{2m}\sum_{j=1}^{m}\theta_j^2 J(θ)=−m1i=1∑m(y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i))))+2mλj=1∑mθj2神经网络代价函数: J ( θ ) = − 1 m ∑ i = 1 m ∑ k = 1 K ( y k ( i ) log ( h θ ( x ( i ) ) ) k + ( 1 − y k ( i ) ) log ( 1 − h θ ( x ( i ) ) ) k ) + λ 2 m ∑ l = 1 L − 1 ∑ j = 1 m ∑ i = 1 m ( θ j i l ) 2 J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}\sum_{k=1}^{K}(y_k^{(i)}\log(h_\theta(x^{(i)}))_k+(1-y_k^{(i)})\log(1-h_\theta(x^{(i)}))_k)+\frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{j=1}^{m}\sum_{i=1}^{m}(\theta_{ji}^{l})^2 J(θ)=−m1i=1∑mk=1∑K(yk(i)log(hθ(x(i)))k+(1−yk(i))log(1−hθ(x(i)))k)+2mλl=1∑L−1j=1∑mi=1∑m(θjil)2优化目标: min Θ J ( Θ ) \underset{\Theta}{\min} J(\Theta) ΘminJ(Θ)
需要计算:
- J ( Θ ) J(\Theta) J(Θ)
- ∂ ∂ Θ i j ( l ) J ( Θ ) \frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta) ∂Θij(l)∂J(Θ), Θ i j ( l ) ∈ R \Theta_{ij}^{(l)}\in\R Θij(l)∈R
如图:
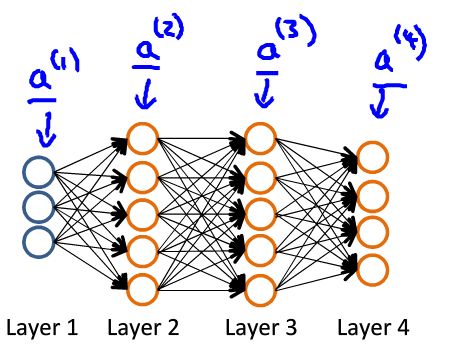
前向传播:
a ( 1 ) = x z ( 2 ) = Θ ( 1 ) a ( 1 ) a ( 2 ) = g ( z ( 2 ) ) z ( 3 ) = Θ ( 2 ) a ( 2 ) a ( 3 ) = g ( z ( 3 ) z ( 4 ) = Θ ( 3 ) a ( 3 ) a ( 4 ) = g ( z ( 4 ) h Θ ( x ) = a ( 4 ) a^{(1)}=x \\ z^{(2)}=\Theta^{(1)}a^{(1)} \\ a^{(2)}=g(z^{(2)}) \\ z^{(3)}=\Theta^{(2)}a^{(2)} \\ a^{(3)}=g(z^{(3}) \\ z^{(4)}=\Theta^{(3)}a^{(3)} \\ a^{(4)}=g(z^{(4}) \\ h_{\Theta}(x)=a^{(4)} a(1)=xz(2)=Θ(1)a(1)a(2)=g(z(2))z(3)=Θ(2)a(2)a(3)=g(z(3)z(4)=Θ(3)a(3)a(4)=g(z(4)hΘ(x)=a(4)
反向传播:
计算: δ j ( l ) \delta_j^{(l)} δj(l)=第 l l l层第 j j j个节点的误差(error);
对于每一个输出单元: δ j ( 4 ) = a j ( 4 ) − y j \delta_j^{(4)}=a_j^{(4)}-y_j δj(4)=aj(4)−yj,写成向量形式为: δ ( 4 ) = a ( 4 ) − y \delta^{(4)}=a^{(4)}-y δ(4)=a(4)−y;由输出层逐级往上计算 δ ( l ) 、 δ ( l − 1 ) … δ ( 2 ) \delta^{(l)}、\delta^{(l-1)}\dots \delta^{(2)} δ(l)、δ(l−1)…δ(2):
δ ( 3 ) = ( Θ ( 3 ) ) T δ ( 4 ) . ∗ g ′ ( z ( 3 ) ) , g ′ ( z ( 3 ) ) = a ( 3 ) . ∗ ( 1 − a ( 3 ) ) δ ( 2 ) = ( Θ ( 2 ) ) T δ ( 3 ) . ∗ g ′ ( z ( 2 ) ) , g ′ ( z ( 2 ) ) = a ( 2 ) . ∗ ( 1 − a ( 2 ) ) \delta^{(3)}=(\Theta^{(3)})^T\delta^{(4)}.*g\prime(z^{(3)}),\qquad g\prime(z^{(3)})=a^{(3)}.*(1-a^{(3)}) \\ \delta^{(2)}=(\Theta^{(2)})^T\delta^{(3)}.*g\prime(z^{(2)}),\qquad g\prime(z^{(2)})=a^{(2)}.*(1-a^{(2)}) δ(3)=(Θ(3))Tδ(4).∗g′(z(3)),g′(z(3))=a(3).∗(1−a(3))δ(2)=(Θ(2))Tδ(3).∗g′(z(2)),g′(z(2))=a(2).∗(1−a(2)) 可以证明(忽略 λ \lambda λ,即 λ = 0 \lambda=0 λ=0): ∂ ∂ Θ i j ( l ) J ( Θ ) = a j ( l ) δ i ( l + 1 ) \frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)=a_j^{(l)}\delta_i^{(l+1)} ∂Θij(l)∂J(Θ)=aj(l)δi(l+1)详细的:
对于训练集 { ( x ( 1 ) , y ( 1 ) ) , … , ( x ( m ) , y ( m ) ) } \{(x^{(1)},y^{(1)}),\dots,(x^{(m)},y^{(m)})\} {(x(1),y(1)),…,(x(m),y(m))};
初始化 Δ i j l = 0 \Delta_{ij}^l=0 Δijl=0,for all l , i , j l,i,j l,i,j

理解:
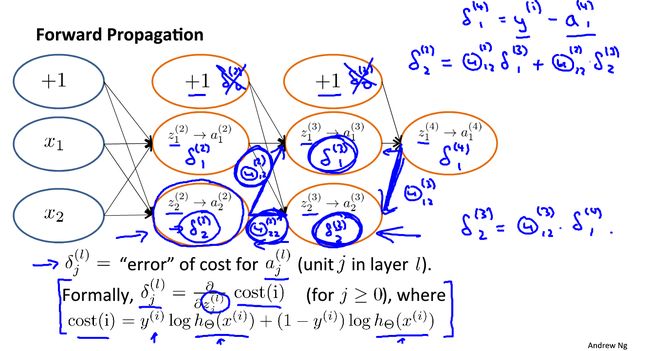
换句话说: δ j ( l ) = ∂ ∂ z j ( l ) c o s t ( i ) \delta_j^{(l)}=\frac{\partial}{\partial z_{j}^{(l)}}cost(i) δj(l)=∂zj(l)∂cost(i) , f o r ( j ≥ 0 ) for(j\geq0) for(j≥0)
where c o s t ( i ) = y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) cost(i)=y^{(i)}\log(h_\theta(x^{(i)}))+(1-y^{(i)})\log(1-h_\theta(x^{(i)})) cost(i)=y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))
δ \delta δ项是代价函数关于这些中间项的偏导数,衡量影响神经网络的权值,进而影响神经网络的输出的程度。
展开参数
梯度检验
随机初始化
together
机器学习细节
模型选择(model selection)
可以依据训练误差和测试误差来评估假设 h θ ( x ) h_\theta(x) hθ(x);
一般来说,我们将数据集划分成训练集(60%)、验证集(20%)和测试集(20%);
在训练集上我们学习参数 θ \theta θ: m i n J ( θ ) minJ(\theta) minJ(θ);
计算训练误差、验证误差:
for linear regression:
J t r a i n ( θ ) = 1 2 m t r a i n ∑ i = 1 m t r a i n ( h θ ( x t r a i n ( i ) ) − y t r a i n ( i ) ) 2 J_{train}(\theta)=\frac{1}{2m_{train}} \sum_{i=1}^{m_{train}}(h_\theta(x_{train}^{(i)})-y_{train}^{(i)})^2 Jtrain(θ)=2mtrain1i=1∑mtrain(hθ(xtrain(i))−ytrain(i))2 J c v ( θ ) = 1 2 m c v ∑ i = 1 m c v ( h θ ( x c v ( i ) ) − y c v ( i ) ) 2 J_{cv}(\theta)=\frac{1}{2m_{cv}} \sum_{i=1}^{m_{cv}}(h_\theta(x_{cv}^{(i)})-y_{cv}^{(i)})^2 Jcv(θ)=2mcv1i=1∑mcv(hθ(xcv(i))−ycv(i))2for logistic regression: J t r a i n ( θ ) = − 1 m t r a i n ∑ i = 1 m t r a i n ( y t r a i n ( i ) log ( h θ ( x t r a i n ( i ) ) ) + ( 1 − y t r a i n ( i ) ) log ( 1 − h θ ( x t r a i n ( i ) ) ) ) J_{train}(\theta)=-\frac{1}{m_{train}}\sum_{i=1}^{m_{train}}(y_{train}^{(i)}\log(h_\theta(x_{train}^{(i)}))+(1-y_{train}^{(i)})\log(1-h_\theta(x_{train}^{(i)}))) Jtrain(θ)=−mtrain1i=1∑mtrain(ytrain(i)log(hθ(xtrain(i)))+(1−ytrain(i))log(1−hθ(xtrain(i)))) J c v ( θ ) = − 1 m c v ∑ i = 1 m c v ( y c v ( i ) log ( h θ ( x c v ( i ) ) ) + ( 1 − y c v ( i ) ) log ( 1 − h θ ( x c v ( i ) ) ) ) J_{cv}(\theta)=-\frac{1}{m_{cv}}\sum_{i=1}^{m_{cv}}(y_{cv}^{(i)}\log(h_\theta(x_{cv}^{(i)}))+(1-y_{cv}^{(i)})\log(1-h_\theta(x_{cv}^{(i)}))) Jcv(θ)=−mcv1i=1∑mcv(ycv(i)log(hθ(xcv(i)))+(1−ycv(i))log(1−hθ(xcv(i))))选择 J c v ( θ ) J_{cv}(\theta) Jcv(θ)最小的模型;
计算测试误差 J t e s t ( θ ) J_{test}(\theta) Jtest(θ);
对于逻辑回归还可以计算误分类率: e r r o r = { 1 , if y i = 1 , h θ ( x ) < 0.5 o r y i = 0 , h θ ( x ) ≥ 0.5 0 , if y i = 1 , h θ ( x ) ≥ 0.5 o r y i = 0 , h θ ( x ) < 0.5 error=\begin{cases} 1,\text{if $y_i=1,h_\theta(x)<0.5\ or\ y_i=0,h_\theta(x)\geq0.5$} \\ 0 ,\text{if $y_i=1,h_\theta(x)\geq0.5\ or\ y_i=0,h_\theta(x)<0.5$}\end{cases} error={1,if yi=1,hθ(x)<0.5 or yi=0,hθ(x)≥0.50,if yi=1,hθ(x)≥0.5 or yi=0,hθ(x)<0.5
方差和偏差(variance VS bias)
如图:
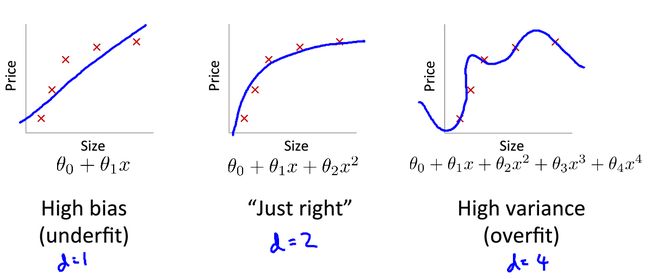
一般来说,欠拟合会产生高偏差;过拟合过产生高方差;
具体来说,当模型欠拟合时,训练误差和验证误差都会较大;当模型过拟合时,训练误差很小,然而验证误差很大,如下图:

如何处理高方差和高偏差问题呢?
一般来说,加入合适的正则化项可以有效地避免过拟合(即高方差)
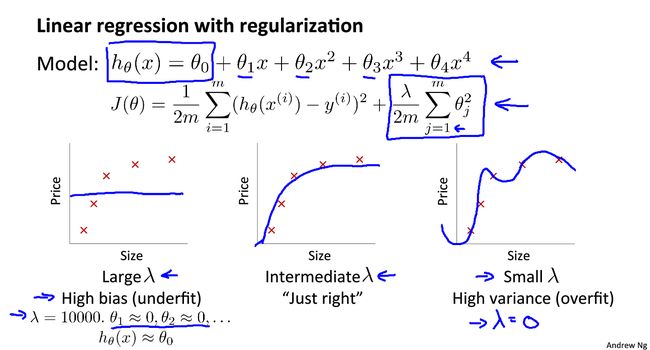
当正则化参数 λ \lambda λ较大时, θ j ≈ 0 \theta_j\approx0 θj≈0(除 θ 0 \theta_0 θ0外),假设函数趋于直线,因而会造成高偏差的问题,导致欠拟合;
当正则化参数 λ \lambda λ较小时,正则化项不起作用,模型会变得过拟合。如图:
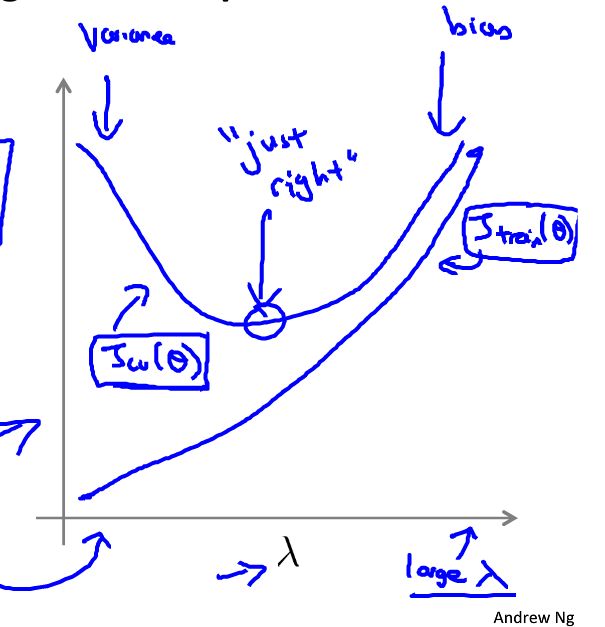
一般的,对于高偏差问题(欠拟合):
- 增加特征个数
- 增加多项式特征
- 降低 λ \lambda λ
对于高方差问题(过拟合):
- 增加训练样本
- 减少特征个数
- 增加 λ \lambda λ
对于神经网络来说,参数越少,越有可能欠拟合;参数越多,网络结构越复杂,越有可能过拟合,应该加入正则化项。
机器学习系统设计
不对称分类的误差评估(skewed classes)
查准率和召回率(Precision和Recall)
y=1 in presence of rare class that we want to detect;
Precision: 预测为正,实际为正的概率
P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP
Recall: 正例被准确预测的概率,也叫查全率,敏感性
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
两者平衡
以逻辑回归为例: 0 ≤ h θ ( x ) ≤ 1 0\leq h_\theta(x) \leq1 0≤hθ(x)≤1
预测y=1,if h θ ( x ) ≥ 0.5 h_\theta(x) \geq 0.5 hθ(x)≥0.5;预测y=0,if h θ ( x ) < 0.5 h_\theta(x) < 0.5 hθ(x)<0.5;
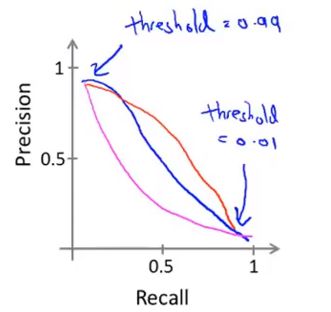
- 如果我们想要比较确信为正例时才判定为正例,那么提高阈值,模型会对应高查准率,低召回率;
- 如果希望避免假阴性,那么降低阈值,模型会对应低查准率,高召回率
PR曲线
F1 Score
F 1 = 2 P R P + R F1=2\frac{PR}{P+R} F1=2P+RPR
支持向量机
优化目标
复习:
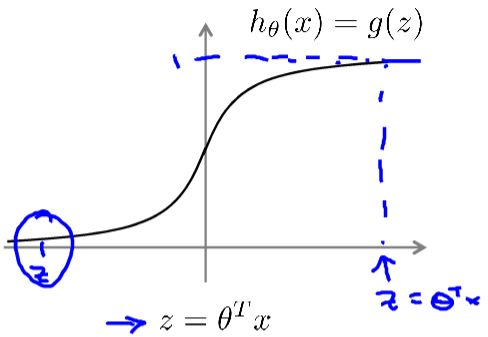
逻辑回归的假设函数: h θ ( x ) = 1 1 + e − θ T x h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}} hθ(x)=1+e−θTx1
if y=1, we want h θ ( x ) ≈ 1 , θ T x > > 0 \text{if y=1, we want }h_\theta(x)\approx1,\theta^Tx>>0 if y=1, we want hθ(x)≈1,θTx>>0
if y=0, we want h θ ( x ) ≈ 0 , θ T x < < 0 \text{if y=0, we want }h_\theta(x)\approx0,\theta^Tx<<0 if y=0, we want hθ(x)≈0,θTx<<0
c o s t ( θ , x ) = − ( y log h θ ( x ) + ( 1 − y ) log ( 1 − h θ ( x ) ) ) cost(\theta,x)=-(y\log h_\theta(x)+(1-y)\log (1-h_\theta(x))) cost(θ,x)=−(yloghθ(x)+(1−y)log(1−hθ(x)))
对逻辑回归的代价函数进行修改:
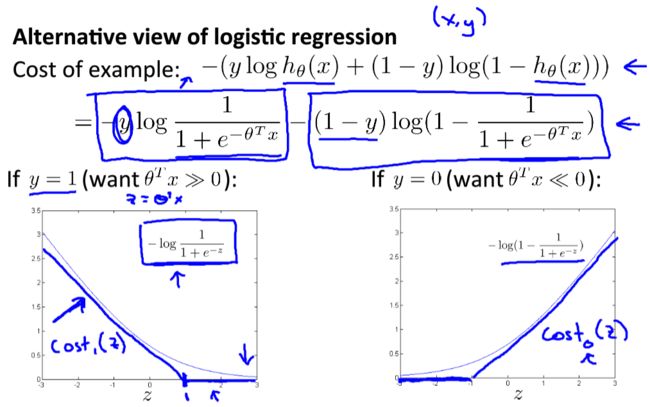
因此,我们可以得到支持向量机的代价函数:
min θ C ∑ i = 1 m [ y ( i ) c o s t 1 ( θ T x ( i ) ) + ( 1 − y ( i ) ) c o s t 0 ( θ T x ( i ) ) ] + 1 2 ∑ i = 1 m θ j 2 \underset{\theta}{\min}C\sum_{i=1}^{m}[y^{(i)}cost_1(\theta^Tx^{(i)})+(1-y^{(i)})cost_0(\theta^Tx^{(i)})]+\frac{1}{2}\sum_{i=1}^{m}\theta_j^2 θminCi=1∑m[y(i)cost1(θTx(i))+(1−y(i))cost0(θTx(i))]+21i=1∑mθj2
公式中的 C C C可以看做是 1 λ \frac{1}{\lambda} λ1,说明支持向量机中更加偏重代价;
间隔最大化
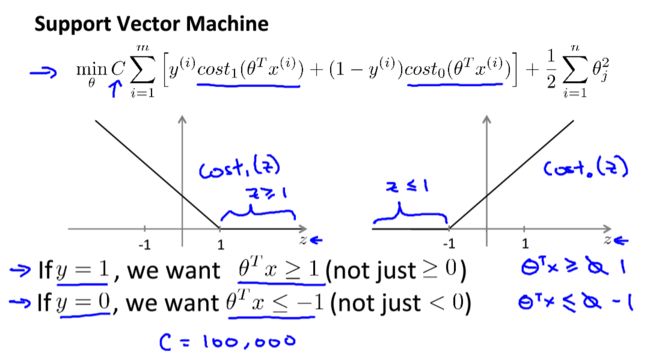
当取一个较大的 C C C值时,当 y ( i ) = 1 y^{(i)}=1 y(i)=1时, θ T x ( i ) ≥ 1 \theta^Tx^{(i)}\geq1 θTx(i)≥1;当 y ( i ) = 0 y^{(i)}=0 y(i)=0时, θ T x ( i ) ≤ − 1 \theta^Tx^{(i)}\leq-1 θTx(i)≤−1;
因此我们可以得到支持向量机的决策边界(Decision Boundary):
m i n θ 1 2 ∑ j = 1 n θ j 2 s.t. θ T x ( i ) ≥ 1 , if y ( i ) = 1 θ T x ( i ) ≤ − 1 , if y ( i ) = 0 \begin{array}{} \underset {\theta} {min} & \frac{1}{2} \sum_{j=1}^{n}\theta_j^2 \\ \text{s.t.}& \theta^Tx^{(i)}\geq1, \quad \text{if} \ y^{(i)}=1 \\ &\theta^Tx^{(i)}\leq-1, \quad \text{if}\ y^{(i)}=0 \end{array} θmins.t.21∑j=1nθj2θTx(i)≥1,if y(i)=1θTx(i)≤−1,if y(i)=0
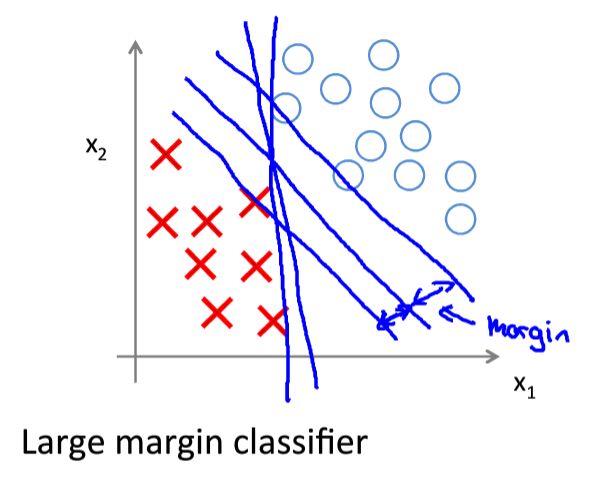
从数学解释上看间隔问题:
1 2 ∑ i = 1 n θ j 2 = 1 2 ( θ 1 2 + … θ n 2 ) 2 = 1 2 ∣ ∣ θ ∣ ∣ 2 \frac{1}{2}\sum_{i=1}^{n}\theta_j^2 = \frac{1}{2}(\sqrt{\theta_1^2+\dots\theta_n^2})^2=\frac{1}{2}||\theta||^2 21i=1∑nθj2=21(θ12+…θn2)2=21∣∣θ∣∣2
简化:n=2
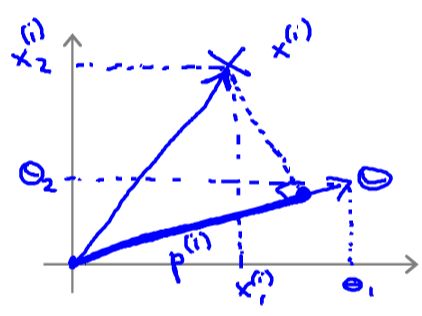
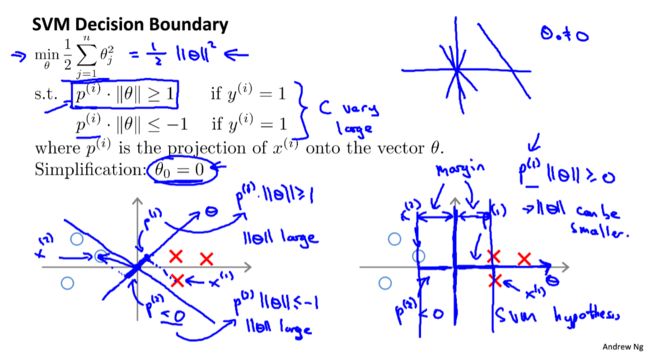
所以有: θ T x ( i ) = p ( i ) ∣ ∣ θ ∣ ∣ = θ 1 x 1 ( i ) + θ 2 x 2 ( i ) \theta^Tx^{(i)}=p^{(i)}||\theta||=\theta_1x_1^{(i)}+\theta_2x_2^{(i)} θTx(i)=p(i)∣∣θ∣∣=θ1x1(i)+θ2x2(i)
决策问题转换为:
核函数

高斯核函数: f i = similarity ( x , l ( i ) ) = exp ( − ∣ ∣ x − l ( i ) ∣ ∣ 2 2 σ 2 ) f_i=\text{similarity}(x,l^{(i)})=\exp(-\frac{||x-l^{(i)}||^2}{2\sigma^2}) fi=similarity(x,l(i))=exp(−2σ2∣∣x−l(i)∣∣2)
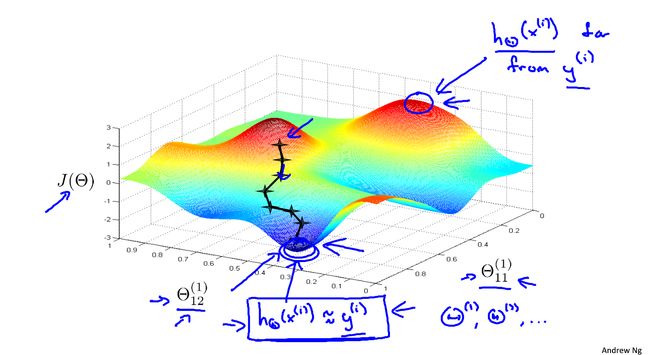
如果 x ≈ l ( i ) x\approx l^{(i)} x≈l(i): f i ≈ exp ( − 0 2 2 σ 2 ) ≈ 1 f_i \approx \exp(-\frac{0^2}{2\sigma^2})\approx 1 fi≈exp(−2σ202)≈1如果 x x x is far from l ( i ) l^{(i)} l(i): f i ≈ exp ( − (larger number) 2 2 σ 2 ) ≈ 0 f_i \approx \exp(-\frac{\text{(larger number)}^2}{2\sigma^2})\approx 0 fi≈exp(−2σ2(larger number)2)≈0
σ 2 \sigma^2 σ2对核函数的影响:
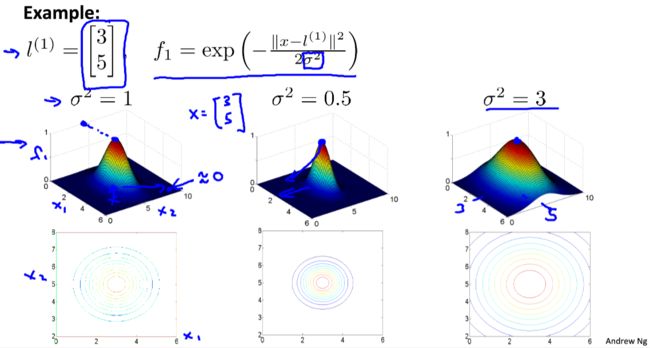
可以看出, σ 2 \sigma^2 σ2越大,变化越缓慢; σ 2 \sigma^2 σ2越大,变化越剧烈。
如何选择标记 l ( i ) l^{(i)} l(i)呢?

SVM将每一个训练样本 ( x ( i ) , y ( i ) ) (x^{(i)},y^{(i)}) (x(i),y(i)),令标记 l ( i ) = x ( i ) l^{(i)}=x^{(i)} l(i)=x(i),对于每一个输入 x x x,计算 f 1 , f 2 , . . . , f m f_1,f_2,...,f_m f1,f2,...,fm,令 f 0 = 1 f_0=1 f0=1,生成新的特征向量 f ∈ R m + 1 f\in\R^{m+1} f∈Rm+1

SVM参数对性能的影响:
逻辑回归和SVM比较
- 如果特征个数n远远大于训练样本个数,建议使用逻辑回归或者线性SVM
- 如果特征个数n较小,训练样本个数适当,建议使用高斯核SVM
- 如果特征个数小,训练样本非常大,建议增加更多特征或者使用逻辑回归或线性SVM