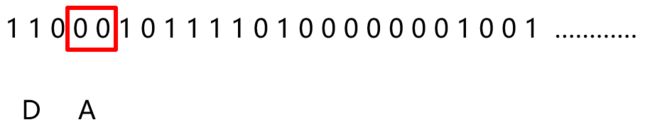无损压缩算法专题——无损压缩算法介绍
一、数据无损压缩的理论——信息论
数据压缩的起源是基于信息论的。信息论之父香农第一次用数学语言阐明了概率与信息冗余度的关系。在1948年发表的论文“通信的数学理论”中,香农指出,任何信息都存在冗余,冗余大小与信息中每个符号的出现概率有关。香农借鉴了热力学的概念,把信息中排除了冗余后的平均信息量称为“信息熵”,并给出了计算信息熵的数学表达式。这篇伟大的论文后来被誉为信息论的开山之作,信息熵也奠定了所有数据压缩算法的理论基础。从本质上讲,数据压缩的目的就是要消除信息中的冗余,而信息熵及相关的定理恰恰用数学手段精确地描述了信息冗余的程度。利用信息熵公式,人们可以计算出信息编码的极限。即在一定的概率模型下,无损压缩的编码长度不可能小于信息熵公式给出的结果。下面是这位帅气的美国数学家的照片,记得大学上课的时候老师PPT摆的是他年轻时的照片,周围同学一个劲地夸他帅,哈哈。
信息量定义:
设信源x由属于集合Am={a1,a2,…,am}的m个可能的符号产生,若信源事件aj的概率为P(aj),则定义事件aj的信息量I(aj):
I(aj)=-log P(aj)
取2为底的对数,则单位为比特(bit),信息量也称自信息。
信源的熵:
一个通信系统并非只传送1个符号,而是多个符号,这就需要定义整个信源符号的平均信息量的大小。我们把自信息的统计平均值——数学期望,称为信源x的熵。熵的大小表示非冗余的不可压缩的信息量。
以上的理论和公式和理论大家只作为一个了解,其实还是很有用的,我们可以根据香农的理论来计算一个特定文件的极限压缩率。
二、数据压缩的必要性及分类
当今信息技术飞速发展。由于数字化的多媒体信息尤其是数字视频和音频信号的数据量特别庞大,如果不对其进行有效的压缩就难以得到实际的应用。像我们平常看的视频和听的音乐都是经过压缩的,最直观的感受就是看视频的时候有蓝光超清、720P等等的清晰度可以选择。MP3也有无损音质和各种有损等级的区别。如果不对数据进行压缩,那么我们平常接触到的大部分文件都是非常庞大的,像视频直播这样的技术应用都会遇到很大的阻碍,所以数据压缩是非常有必要的。
那么问题来了,数据可以被无限压缩吗?答案可定是不能的,我们平时都会发现,被压缩过的文件就很难再被压缩了,从本质上讲,数据压缩的目的就是要消除信息中的冗余,数据压缩只不过是把海绵中的水挤压出来,再怎么用力都无法把海绵都挤的消失。
下面我们来看看数据压缩的分类:
无损压缩:完全还原被压缩的数据,适用于普通文件和可执行文件等不能容忍数据丢失的场合,压缩率比较小。
有损压缩:不能完全还原被压缩的数据,适用于多媒体文件等可容忍一定数据丢失的场合,压缩率比较大。
为什么数据压缩分为这么多的种类,统一用一种压缩算法不行吗?当然是不行的,因为面向不同的应用场合是有不同的应用需求的,一种算法在这种场合好用并不代表在另外一个场合就一定也好用,所谓“术业有专攻”说的就是这个道理。既然分为那么多的种类,就必然需要一些定性的指标来评判一个压缩算法的好坏。下面是一些压缩算法的性能指标:
压缩比:压缩前的数据大小和压缩后的数据大小之比。
数据质量:无损压缩不存在数据质量问题,而有损压缩数据失真情况很难量化,只能对测试的数据进行估计。
软硬件系统:有些硬件系统有数据压缩模块,与软件系统相比速度快更快。但软件系统灵活度更高。
压缩/解压速度:不同场合对速度性能有不同的要求。
三、压缩编码
(1)香农-范诺编码(Shannon–Fano coding)
最早阐述和实现“从上到下”的熵编码方法的人是Shannon(1948年)和Fano(1949年),因此称为香农-范诺(Shannon- Fano)编码法。编码步骤如下:
编码举例
现有A,B,C,D和E共5类符号,出现的次数如下表,试着对这40个符号进行香农范诺编码:
通常情况下每个符号需要用3个比特位来编码表示,现在对这些符号进行香农-范诺编码。
①根据符号出现的概率对符号进行降序排列后,分出最均匀的两部分,然后在中间画一条红线分开两部分。可能有人会问最均匀是怎么判定的,简单的一个判定就是这两部的“出现次数”差值最小。举个例子,从B和C间划开两部分后第一部分“出现次数”为15+7=22,第二部分为7+6+5=18,差值为22-18=4;若从C、D间划开两部分后第一部分“出现次数为”15+7+7=29,第二部分为6+5=11,差值为29-11=18;显然从B和C间划开是差值最小的,所以从这里划开。
划开两部分之后第一部分分配一个比特位0,第二部分分配一个比特位1,如下表所示:
②以此类推,将上一次分出来的各部分再进行划分,继续分配相应的比特位,于是可以得到如下的表格:
③于是得出了每个符号应该分配的编码A(00)、B(01)、C(10)、D(110)、E(111),接下来就可以对比一下压缩性能了。
压缩前编码位数:N1 = 40 x 3 = 120
压缩后编码位数:N2 = 30 + 14 + 14 + 18 + 15 = 91
压缩率: (120-91) / 120 ≈ 24.2%
问题思考:假设现在就有一个这样的文本文件等待我们去压缩,我们把这些字符统计一番然后编码后,我们再去解压的时候会遇到一个什么样的问题呢?在突然对一个文件进行解压的时候,很明显在解压的时候根本就不知道每个字符是对应什么样的编码的,就没法解压啦。所以我们需要在解压的时候知道对应关系,那么自然就需要在压缩的时候把对照表写到压缩文件里面去,告诉解压时程序每个编码对应应该解释出什么字符,类似于下图这样。
译码过程
既然讲了编码肯定也要讲讲解压文件时怎么去译码,译码时需要先获取编码码表得知每种编码所对应的真实字符,然后进行译码,因为香农-范诺编码属于前缀码,即任意一个字符的编码都不可能是另外一个字符的前缀,所以译码过程中不会导致出错。下面举个例子来理解。
我们读取这个解压文件的编码对照表,得出如下的表格:
大家很容易发现一个问题,两位二进制有4种组合方式“00”、“01”、“10”、“11”,为什么编码的时候上面只用了三种却没用“11”这种组合?原因很简单,我们可以先假设有“11”这种组合的码字而且它代表的字符是“F”,那么问题来了,当译码的时候读到“11”这两个比特的数据时,我到底译码成“F”这个字符还是继续向后再读一位比特位去译码成“D”或者“E”呢?所以这里就有个冲突问题,“前缀码”的引入就是为了解决这个问题。
理解了“前缀码”的概念之后,我们开始读取数据进行解压译码,从茫茫的数据流中,我们先读到“110”,发现表里能匹配上,然后译码成“D”,再读再与表里的字符进行匹配,依此类推,直到把整个文件数据全部解压完。
到这里整个过程就已经结束了,有个问题还是要说下,如果保存的压缩数据中有个别比特位反转,对整体数据会有什么样的影响呢?我们假设以上的数据中某个位反转,发现之后的大片数据可能都会译码错误。究其原因是因为每个字符的编码长度是不一致的,所以出现这种状况会有很大影响,
(2)霍夫曼编码(Huffman coding)
一种 “从下到上”的编码方法。待编码的元素出现的次数越多,其编码的位数就越少,霍夫曼编码被广泛用在JPEG, MPEG, H.26X等各种信息编码标准中。编码步骤如下图:
编码举例
试着对有30个符号的字符串:BABACACADADABBCBABEBEDDABEEEBB,进行霍夫曼编码。
①首先我们照符号出现先统计一下这些字符的信息,如下表:
②将这些符号按概率大小降序排列,然后选择两个概率最小的符号,这里明显是C和D,组成一个节点P1,后面跟上一个小括号里面填上权重为3+4=7,如下图所示:
③根据上一次的结果,存在B、A、E、P1这4个节点,然后再选出两个权重(次数)最小的符号,即E和P1,然后构成新的节点P2,同样后面写上权重为5+7=12,依此类推,操作到最后只剩下一个节点为止。如下面两幅图所示:
④接下来分配码字,给每一条节点与节点之间的连线都要分配一个比特位,分配规则是给权重小的分配0,另一个权重大的分配1,如下图所示,其实0和1互换过来分配也是可以的,这没什么关系。
⑤从右往左顺着字符的枝节读下去就是该字符应该分配的码字了,A(10)、B(11)、C(010)、D(011)、E(00)。译码方法和前面介绍的香农范诺编码是类似的。学过数据结构的朋友肯定能看出来,这其实就是一颗二叉树,只不过转了90度而已,霍夫曼编码采用最优二叉树的形式进行编码,是理论上的最优前缀编码。
(3)行程长度编码(Run-Length Coding)
计算出相同值重复出现的次数,对相同的数据只编码一次。在JPEG,MPEG,H.261和H.263等压缩方法中,RLE用来对图像数据变换和量化后的系数进行编码。
这种编码方式有个很明显的缺陷,当待编码的数据中重复块很少时,这种编码方式会使得压缩后的数据比原始数据还要大,所以在实际应用中都会做相应的改进。
四、词典编码
(1)词典编码的概念和分类
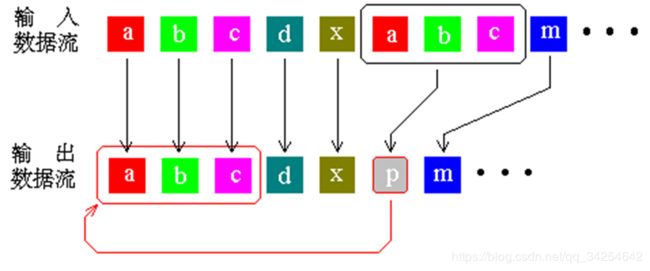
词典编码的实质就是用一些短的索引来替换重复出现的数据段。LZ系列算法是最具代表性的词典编码算法。同样,举个生动形象的例子:
看到第一行写的是“吃葡萄不吐葡萄皮”,聪明的你一定猜到下面一行写的是“不吃葡萄倒吐葡萄皮”了。为什么我下面一行没写字上去大家也能知道是什么内容?因为每个图形都代表了一串特定的字符,词典编码也是这个道理。再举个程序员懂的例子,C语言中用一个指针来指向一个字符串,我们输出字符串的时候只需要知道这个指针就行了,那么这个指针就是代表了这一大串的字符,就相当于是数据压缩了。
第一类编码算法
①用已经出现过的字符串替代重复的部分。
②编码器的输出仅仅是指向早期出现过的字符串的“指针”。
第二类编码算法
①从输入的数据中创建一个“短语词典”。
②编码器输出词典中的短语“索引号”。
(2)LZSS算法原理(第一类编码)
LZSS由LZ77改进而来,又称“滑动窗口压缩”,该算法将一个虚拟的,可以跟随压缩进程滑动的窗口作为词典,要压缩的字符串如果在该窗口中出现,则输出其出现位置和长度,没出现则原样输出字符。
编码步骤
编码格式
如果匹配串的长度比指针本身的长度长就输出指针,否则就输出真实字符。由于输出的压缩数据流中包含有指针和字符本身,为了区分它们就需要有额外的标志位。下面举个例子,只是做个示例,实际应用不一定这么用。
我们假设编码格式为8个字节一组,第1字节用来做标记,标记后面7个数据哪些是真实的数据,哪些是指针。
蓝色部分的是真实数据,直接输出就可以了,后面的0x03 0x03为一组,表示在前向缓冲区的第3个数据处开始匹配3个字符,于是匹配到0x41、0x42、0x43,接下来两个数据一样的道理。 最后解压出来如下图的数据。
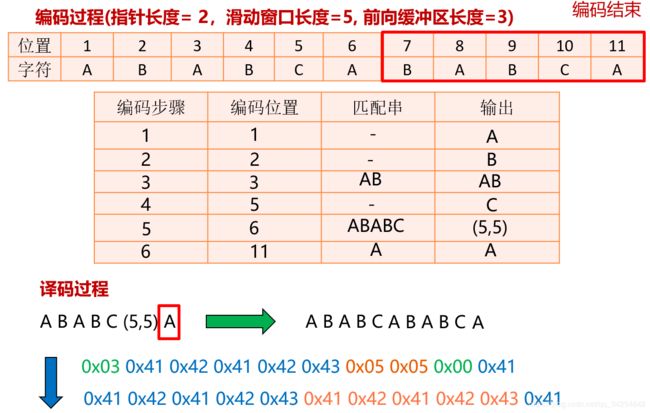
举个完整过程的例子:
(3)LZW算法原理(第二类编码)
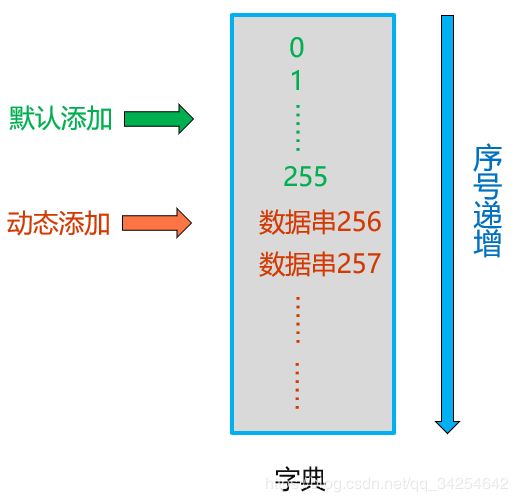
LZW由LZ78的改进而来,编/译码过程就是不断往“字典”中添加新的数据串,并且对新的数据串进行编号,输入是字符流,输出是“字典”中的序号。
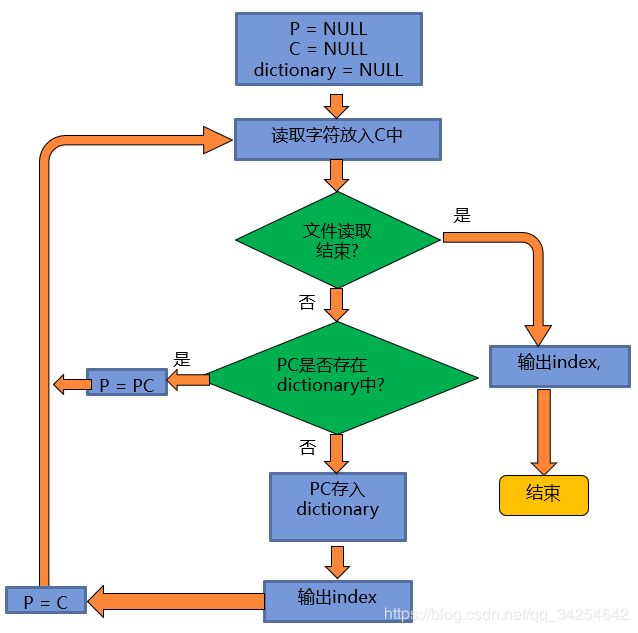
LZW编码步骤
P:数据串前缀, C:当前字符, PC:P和C字符串的连接。
(4)LZ系列算法比较
五、总结
压缩算法种类繁多,需要针对不同的场合选择不同的算法,没有最好,只有最适合的算法。写到这里也很累了现在,在这一篇只做算法的介绍,之后的一段时间里会逐步用代码去实现以上所述的算法,并研究在实际项目中的灵活运用。